[#118] Add Eisenstein integers module #121

rockbmb · 2018-08-09T02:52:01Z

This will close #118, but at the moment it's still a work in progress.

EDIT:

Fix divModE, and write more extensive tests for Euclidean division (in the commutative ring of Eisenstein integers).
Write an isPrime :: EisensteinInteger -> Bool function.
Add a gcdE :: EisensteinInteger -> EisensteinInteger -> EisensteinInteger function.
Write a factorize :: EisensteinInteger -> [(EisensteinInteger, Int)] function.
Add a way to generate all Eisenstein primes, similar to what is done with GaussianIntegers. This has been split from the isPrime bulletpoint as it will not be a trivial task.

All of these features will require

Tests
and
Benchmarks.

There are other functions of use to be added, but these are the most important.

rockbmb · 2018-08-09T05:25:15Z

Math/NumberTheory/EisensteinIntegers.hs

+    -- same quadrant as @(2*a - b) / 2 + (b * ι) / 2@, and this one in the
+    -- same as @(2*a - b) + b * ι@. Divisions or floating points are not
+    -- necessary.
+    abs z@(x :+ y) = abs' (2*x - y) x


@Bodigrim I just realized this is wrong. First of all, what does one take the absolute value of an Eisenstein integer, abs n, to be? Is it an E. integer n' with the same magnitude such that (signum n) * (abs n) == n', as it is with Gaussian integers?

With G. integers, there are four units, one for each quadrant of the complex plane, and signum always returns one of those.
However, the commutative ring of Eisenstein integers has 6 units ({1, -1, ω, -ω, ω², -ω²}), one cannot assign each to a regular Cartesian quadrant. Do we divide the complex plane into 6 parts when dealing with Eisenstein integers?

Exactly, there are 6 sextants, 60 degrees each. abs should put its argument into the first one.

rockbmb · 2018-08-10T06:16:55Z

Math/NumberTheory/EisensteinIntegers.hs

-    -- necessary.
-    abs z@(x :+ y) = abs' (2*x - y) x
+    abs z@(a :+ b)
+        | a == 0 && b == 0                                  = z            -- origin


@Bodigrim There is probably a better way to do this. I did not want to use phase here because it brings Double's precision issues as the numbers get larger.

abs $ 10^n :+ (10^n - 1) will probably give the wrong result for some large n, but for now it works. I'll think of a way to do this check without phases later.

The smaller example, for which Double-based implementation of abs gives a wrong result is 3640002541000001 + 3640002541000000 * ω. It makes sense to add this case to test suite.

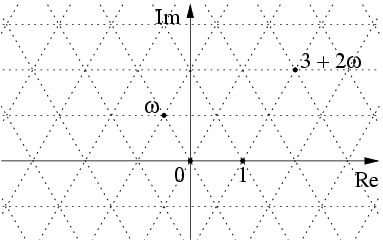
You can derive rules how to determine sextant from this picture:

For instance, a:+b lies in the first sextant when a > b >= 0, in the second when b >= a > 0, in the third when b > 0 >= a, etc.

@Bodigrim I derived those bounds as well, but I got wrong results the first time because I was multiplying by the wrong unit (i.e. perfoming an incorrect rotation in the plane), so I decided to make it work first with Data.Complex.phase and then think about it some more.

rockbmb · 2018-08-11T02:24:34Z

@Bodigrim unrelated to the issue, isn't it about time the package is moved away from GHC==7.10.3?

Bodigrim · 2018-08-11T09:48:56Z

@Bodigrim unrelated to the issue, isn't it about time the package is moved away from GHC==7.10.3?

The latest release still supports GHC 7.8 and the upcoming one will be the first which doesn't. I am not keen to drop support of GHC 7.10 as well that soon. Is there anything particularly annoying in 7.10 from your point of view?

rockbmb · 2018-08-11T19:18:41Z

@Bodigrim there have been two major releases since then (8, 8.2, 8.4) with a fourth one coming soon (8.6), a few breaking changes like type families and type application already exist and CPP never gets easier. Does this package always support the 5 latest releases? If so, I take back what I said.

Bodigrim · 2018-08-11T20:11:27Z

IMHO with a new, half-year release cycle of GHC it is preferable to support more than three last versions, as long as it does not cause too much pain. I do not like CPP pragmas and feel excited each time when I can get rid of them, of course :)

Ubuntu 16.04 LTS was shipped with GHC 7.10 and I have plenty of them. Of course, nowadays we rarely use GHC from system distribution, but I mean, 7.10 was not that long ago.

Alternatively, as a last resort, one can expose new functionality for newer GHCs only:

  if impl(ghc >= 8)
    exposed-modules:
      Math.NumberTheory.BrandNewStuff

(I wrestle against temptation to use this trick to implement ideas described in #71.)

That said, the upcoming release (fall 2018) will still work with GHC 7.10, but looking at GHC release timeline it looks reasonable to drop its support afterwards.

The `Num EisensteinInteger` instance now works properly, and there is now division over the Euclidean domain of `EisensteinIntegers`.

rockbmb · 2018-08-15T21:03:51Z

Status update: right now, the division algorithm for EisensteinIntegers isn't working (fails a simple test), but the plan for the PR is as follows:

EDIT: I've moved the list to the PR's opening comment.

The tests for `divModE` fail, the reason for the function's incorrect behavior is under investigation. `divModE'` is a similar division algorith used for `GaussianIntegers` that works, if no other way to fix the current process used by `divModE`, `divModE'` will be used instead.

Bodigrim · 2018-08-22T12:11:44Z

Working on #129, I discovered that the general case of quadratic modular equations is harder than I thought. But there is a simple method, when a coefficient at x^2 is 1. Here is how it works for Eisenstein primes.

Each prime of form 3n+1 is actually of form 6k+1.
We have (z+3k)^2 = z^2 + 6kz + 9k^2 = z^2 + (6k+1)z - z + 9k^2 = z^2 - z + 9k^2 (mod 6k+1).

Our goal is to solve z^2 - z + 1 = 0 (mod 6k+1). We have:
z^2 - z + 9k^2 = 9k^2 - 1 (mod 6k+1)
(z+3k)^2 = 9k^2-1 (mod 6k+1)
z+3k = sqrtMod(9k^2-1)
z = sqrtMod(9k^2-1) - 3k

For example, let p = 7, then k = 1. Square root of 9*1^2-1 modulo 7 is 1.
And z = 1 - 3*1 = -2 = 5 (mod 7). Truly, norm(5 :+ 1) = 25 - 5 + 1 = 21 = 0 (mod 7).

rockbmb · 2018-08-22T17:41:16Z

@Bodigrim sorry, where did this

We have (z+3k)^2 = z^2 + 6kz + 9k^2 = z^2 - z + 9k^2 (mod 6k+1).

come from?

Bodigrim · 2018-08-22T18:01:22Z

I update the previous comment. Is it more clear now?

rockbmb · 2018-08-22T18:14:41Z

@Bodigrim Yes, but it was clear from the start, no problem there. What I mean is, was that fact just stated to be used afterwards?

rockbmb · 2018-08-24T18:22:00Z

@Bodigrim I've completed all the tasks in the list I wrote. I'm going to be adding more comments and benchmarks/tests but as far as code goes the PR is ready to be reviewed.

There is now a test to verify that a factorisation only produces primary Eisenstein prime factors.

Fixes a typo for `Math.NumberTheory.EisensteinInteger.associates` and rewords the comment for `Math.NumberTheory.EisensteinInteger.primes`, as well as a few other comments.

Bodigrim · 2018-08-25T18:32:41Z

Math/NumberTheory/EisensteinIntegers.hs

+    fromInteger n = n :+ 0
+    signum z@(a :+ b)
+        | a == 0 && b == 0 = z               -- hole at origin
+        | otherwise        = z `divE` abs z


It would be nice to avoid division here (and for Gaussian integers as well, generally speaking). To do not repeat a long pattern-matching we can have a single function absSignum :: EisensteinInteger -> (EisensteinInteger, EisensteinInteger) and abs = fst . absSignum, signum = snd . absSignum.

Bodigrim · 2018-08-25T18:34:44Z

Math/NumberTheory/EisensteinIntegers.hs

+associates :: EisensteinInteger -> [EisensteinInteger]
+associates e = map (e *) ids
+
+-- | Takes an Eisenstein prime whose norm is of the form @3k + 1@ with @k@


Is it safe to say that its norm is of form 6k+1? It would be more specific.

It is not clear from the comment, what does this function return?

As below, it is not safe to say its norm is of the form 6k + 1 because of 1 - ω and 2.

Bodigrim · 2018-08-25T18:36:43Z

Math/NumberTheory/EisensteinIntegers.hs

+norm (a :+ b) = a*a - a * b + b*b
+
+-- | Checks if a given @EisensteinInteger@ is prime. @EisensteinInteger@s
+-- whose norm is a prime congruent to @0@ or @1@ modulo 3 are prime.


I suggest to write about norms modulo 6, because it is more specific.

I don't think it is necessary. Counting with associates, there are 6 primes with norm 3 (associates of 1 - ω), and 6 with norm 4 (associates of 2). These norms are not congruent to 0 or 1 modulo 6.

Bodigrim · 2018-08-25T18:38:15Z

Math/NumberTheory/EisensteinIntegers.hs

+findPrime :: Integer -> EisensteinInteger
+findPrime p = case Moduli.sqrtModMaybe (9*k*k - 1) (FieldCharacteristic (PrimeNat . integerToNatural $ p) 1) of
+    Nothing      -> error "findPrime: argument must be prime p = 6k + 1"
+    Just sqrtMod -> gcdE (p :+ 0) ((sqrtMod - 3 * k) :+ 1)


Can we use the same approach as for Gaussian integers here? Complex GCD is very expensive.

I forgot to leave a note to myself to figure out why, but using the same process as Gaussian integers makes this process fail. Regarding the complexity of gcdE, I found this link. Worth considering.

EDIT: Previous link has bitrotten, will keep it for reference. I was trying to refer to this work: Efficient algorithms for the gcd and cubic residuosity in the ring of Eisenstein integers

@Bodigrim by the way, would you mind reading the paper I linked here and telling me how Lemma 1 can be practically implemented as an approximate norm function, please?

I did not understand the process behind it, only that it is possible and crucial for a fast Eisenstein gcd.

Nevermind, I understood what was needed and the latest commit implements it.

I didn't benchmark it directly, but benchmarks for findPrime have gotten considerably slower, and the only thing used by that function which changed was gcdE. This change might not be worth it after all. Integer bit shifting might be too expensive not to do in-place.

I tried using the same method that Math.NumberTheory.GaussianIntegers.findPrime uses, and as before, it does not work.

Bodigrim · 2018-08-25T18:40:56Z

benchmark/Math/NumberTheory/GaussianIntegersBench.hs

@@ -21,6 +21,6 @@ benchTau n = bench (show n) $ nf (\m -> sum [tau (x :+ y) | x <- [1..m], y <- [0

 benchSuite :: Benchmark
 benchSuite = bgroup "Gaussian"
-  [ bgroup "findPrime" $ map benchFindPrime [1000033, 10000121, 100000037, 1000000009, 10000000033, 100000000057, 1000000000061, 10000000000037]
+  [ bgroup "findPrime" $ map benchFindPrime [1000033, 10000121, 100000037, 1000000021, 10000000033, 100000000057, 1000000000061, 10000000000037]


What was the reason for change?

Typo. I was using this file by mistake to write newer primes with the same order of magnitude but of the form 3k + 1 which Eisenstein integers require, instead of 4k + 1, which is what Gaussian integers require.

Bodigrim · 2018-08-25T18:42:14Z

Overall it looks superb incredibly cool. Thanks for a valuable contribution.

Using a method described in [Efficient algorithms for the gcd and cubic residuosity in the ring of Eisenstein integers] (https://core.ac.uk/download/pdf/82554035.pdf), the algorithm used to calculate the `gcd` between Eisenstein integers was refactored.

Bodigrim · 2018-08-27T20:06:59Z

Math/NumberTheory/EisensteinIntegers.hs

+
+instance Num EisensteinInteger where
+    (+) (a :+ b) (c :+ d) = (a + c) :+ (b + d)
+    (*) (a :+ b) (c :+ d) = (a * c - b * d) :+ (b * c + a * d - b * d)


It is worth to save one multiplication: b * (c - d) + a * d or b * c + (a - b) * d.

Bodigrim · 2018-08-27T20:09:06Z

Math/NumberTheory/EisensteinIntegers.hs

+    go !n !z | r == 0    = go (n + 1) q
+             | otherwise = (n, abs z)
+      where
+        (q, r) = divModE (z * (2 :+ 1)) 3


Can we use quotEvenI smth 3 instead of divModE? It may be worse to inline and reduce multiplication by 2 :+ 1 to avoid any multiplications: (a :+ b) * (2 :+ 1) = (a + a - b) :+ (a + b).

Bodigrim

My impression is that algorithms for GCD, as in paper cited, shine for huge numbers only and require super efficient bit fiddling, which is not easily accessible from Haskell. I agree that it may be not worth of it.

Bodigrim · 2018-08-27T20:13:42Z

Math/NumberTheory/EisensteinIntegers.hs

+    go !x !i | x == 0    = i
+              | otherwise = go x' (i + 1)
+      where
+        x' = shift x (-1)


I suspect to achieve desired performance one should use GHC.Integer.GMP.Internals.sizeofBigNat# and GHC.Exts.clz#.

Bodigrim · 2018-08-27T20:14:42Z

Math/NumberTheory/EisensteinIntegers.hs

+
+    mask :: Integer
+    mask | m < 6 = 0b111111
+         | otherwise = foldl (\acc bit -> setBit acc bit) zeroBits [m - 6 .. m - 1]


Isn't it faster to shift 0b111111 by m-6 positions?

Bodigrim · 2018-08-27T20:17:16Z

Math/NumberTheory/EisensteinIntegers.hs

+gcdE' α β =
+    let (j1, γ) = divideByThree α
+        (j2, δ) = divideByThree β
+        g       = (1 :+ (-1)) ^ min j1 j2


This may be expensive. It may be faster to precompute first 3 powers and resort to exponentiation only in rare case min j1 j2 > 3.

rockbmb · 2018-08-28T16:31:11Z

@Bodigrim the last set of changes improves things, but is still slower than before. An alternative is to check the numbers composing the Eisenstein integer, and only use the new algorithm for magnitudes larger than 10^10 (arbitrarily chosen).

Bodigrim · 2018-08-28T18:30:33Z

I think it is better to revert to the simple GCD algorithm for now.

rockbmb · 2018-08-28T19:38:49Z

@Bodigrim alright. In any case, I fixed things up in my last commit in case this ever becomes useful. Furthermore, it is also generalizable to Gaussian integers.

EDIT: I'll still be using gcdE in findPrime because the method from the Gaussian findPrime does not work.

The `Math.NumberTheory.EisensteinIntegers.gcdE` function was changed to use the previous algorithm.

rockbmb · 2018-08-28T20:52:35Z

@Bodigrim the PR is good to go on my end.

rockbmb · 2018-08-28T22:44:20Z

@Bodigrim after this is merged, since #131 has also been merged, I'll make a new PR to use solveQuadratic both with Eisenstein and Gaussian integers' findPrime.

Bodigrim · 2018-08-29T18:37:05Z

since #131 has also been merged, I'll make a new PR to use solveQuadratic
both with Eisenstein and Gaussian integers' findPrime

The exposed interface of solveQuadratic is quite expensive to use in tight loops, so I suggest to leave findPrime as is.

Merged, awesome!

rockbmb force-pushed the eisenstein-integers branch from 6bd0649 to bd3e9e3 Compare August 9, 2018 03:15

rockbmb commented Aug 9, 2018

View reviewed changes

rockbmb commented Aug 10, 2018

View reviewed changes

rockbmb force-pushed the eisenstein-integers branch 3 times, most recently from f7edc1a to bf881e7 Compare August 12, 2018 06:49

rockbmb added 2 commits August 13, 2018 00:01

[Bodigrim#118] Add Eisenstein integers module

aa1a97e

[Bodigrim#118] Add division for EisensteinIntegers

3b481b2

The `Num EisensteinInteger` instance now works properly, and there is now division over the Euclidean domain of `EisensteinIntegers`.

rockbmb force-pushed the eisenstein-integers branch from bf881e7 to 76d2415 Compare August 13, 2018 00:02

rockbmb force-pushed the eisenstein-integers branch 2 times, most recently from ed67f86 to f5352ef Compare August 16, 2018 00:54

rockbmb added 2 commits August 16, 2018 01:17

[Bodigrim#118] Fix Eisenstein integer's division algorithm

ec8b748

rockbmb force-pushed the eisenstein-integers branch 3 times, most recently from 4691ff5 to 4c51cc8 Compare August 16, 2018 03:45

Bodigrim mentioned this pull request Aug 17, 2018

Euclidean rings #128

Closed

rockbmb force-pushed the eisenstein-integers branch from 7db763c to 7f2f5c9 Compare August 22, 2018 15:59

rockbmb added 2 commits August 22, 2018 17:06

[Bodigrim#118] Add primality testing for Eisenstein integers

7c83b92

[Bodigrim#118] Add gcd for Eisenstein integers

673db26

rockbmb force-pushed the eisenstein-integers branch from 7f2f5c9 to 673db26 Compare August 22, 2018 16:06

rockbmb added 6 commits August 24, 2018 20:33

[Bodigrim#118] Add one more factorisation test

46cb513

There is now a test to verify that a factorisation only produces primary Eisenstein prime factors.

[Bodigrim#118] Add test to verify sign of primes produced by primes

d9a9b9f

[Bodigrim#118] Improve comment for factorise

e006565

[Bodigrim#118] Add comment to quotEvenI

71dd575

[Bodigrim#118] Improve findPrime's comment

9877dc0

[Bodigrim#118] Add Eisenstein integer benchmark module

7996d9a

rockbmb force-pushed the eisenstein-integers branch from b903d18 to 863110e Compare August 25, 2018 01:38

Fix comments

ac7dad4

Fixes a typo for `Math.NumberTheory.EisensteinInteger.associates` and rewords the comment for `Math.NumberTheory.EisensteinInteger.primes`, as well as a few other comments.

rockbmb force-pushed the eisenstein-integers branch from 863110e to ac7dad4 Compare August 25, 2018 02:31

Bodigrim reviewed Aug 25, 2018

View reviewed changes

rockbmb added 3 commits August 25, 2018 22:39

Fixes from review

2dd510e

[Bodigrim#118] Made Eisenstein GCD faster (WIP)

fcee5b1

rockbmb force-pushed the eisenstein-integers branch from 635be23 to 1b5306c Compare August 27, 2018 00:03

Bodigrim reviewed Aug 27, 2018

View reviewed changes

Fixes from second review

fe534b0

[Bodigrim#118] Revert GCD's algorithm

112fd43

The `Math.NumberTheory.EisensteinIntegers.gcdE` function was changed to use the previous algorithm.

rockbmb force-pushed the eisenstein-integers branch from ce6085f to 112fd43 Compare August 28, 2018 20:26

Bodigrim merged commit e31769d into Bodigrim:master Aug 29, 2018

rockbmb deleted the eisenstein-integers branch October 18, 2018 22:03

[#118] Add Eisenstein integers module #121

[#118] Add Eisenstein integers module #121

Conversation

rockbmb commented Aug 9, 2018 • edited Loading

rockbmb Aug 9, 2018 • edited Loading

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

rockbmb commented Aug 11, 2018

Bodigrim commented Aug 11, 2018

rockbmb commented Aug 11, 2018

Bodigrim commented Aug 11, 2018 • edited Loading

rockbmb commented Aug 15, 2018 • edited Loading

Bodigrim commented Aug 22, 2018 • edited Loading

rockbmb commented Aug 22, 2018

Bodigrim commented Aug 22, 2018

rockbmb commented Aug 22, 2018 • edited Loading

rockbmb commented Aug 24, 2018 • edited Loading

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

rockbmb Aug 25, 2018 • edited Loading

Choose a reason for hiding this comment

Choose a reason for hiding this comment

rockbmb Aug 25, 2018 • edited Loading

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

rockbmb Aug 27, 2018 • edited Loading

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Bodigrim commented Aug 25, 2018 • edited Loading

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Bodigrim left a comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

rockbmb commented Aug 28, 2018

Bodigrim commented Aug 28, 2018

rockbmb commented Aug 28, 2018 • edited Loading

rockbmb commented Aug 28, 2018

rockbmb commented Aug 28, 2018 • edited Loading

Bodigrim commented Aug 29, 2018

rockbmb commented Aug 9, 2018 •

edited

Loading

rockbmb Aug 9, 2018 •

edited

Loading

Bodigrim commented Aug 11, 2018 •

edited

Loading

rockbmb commented Aug 15, 2018 •

edited

Loading

Bodigrim commented Aug 22, 2018 •

edited

Loading

rockbmb commented Aug 22, 2018 •

edited

Loading

rockbmb commented Aug 24, 2018 •

edited

Loading

rockbmb Aug 25, 2018 •

edited

Loading

rockbmb Aug 25, 2018 •

edited

Loading

rockbmb Aug 27, 2018 •

edited

Loading

Bodigrim commented Aug 25, 2018 •

edited

Loading

rockbmb commented Aug 28, 2018 •

edited

Loading

rockbmb commented Aug 28, 2018 •

edited

Loading