圆内一个 有效切割 ,符合以下二者之一:
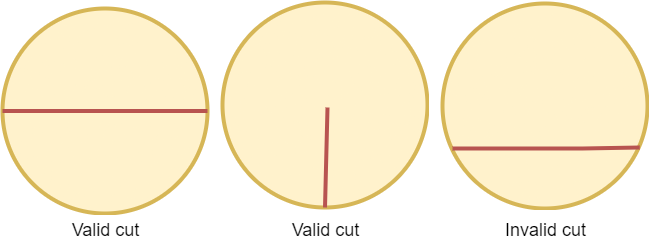
- 该切割是两个端点在圆上的线段,且该线段经过圆心。
- 该切割是一端在圆心另一端在圆上的线段。
一些有效和无效的切割如下图所示。
给你一个整数 n ,请你返回将圆切割成相等的 n 等分的 最少 切割次数。
示例 1:
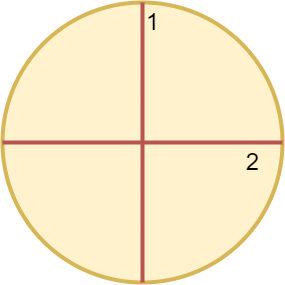
输入:n = 4 输出:2 解释: 上图展示了切割圆 2 次,得到四等分。
示例 2:
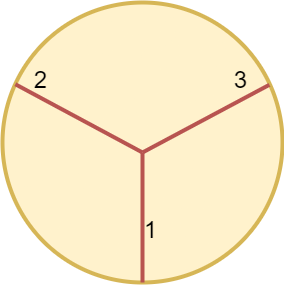
输入:n = 3 输出:3 解释: 最少需要切割 3 次,将圆切成三等分。 少于 3 次切割无法将圆切成大小相等面积相同的 3 等分。 同时可以观察到,第一次切割无法将圆切割开。
提示:
1 <= n <= 100
- 当
$n=1$ 时,不需要切割,即切割次数为$0$ ; - 当
$n$ 为奇数时,不存在共线的情况,最少需要$n$ 次切割; - 当
$n$ 为偶数时,可以两两共线,最少需要$\frac{n}{2}$ 次切割。
综上,可以得到:
时间复杂度
class Solution:
def numberOfCuts(self, n: int) -> int:
return n if (n > 1 and n & 1) else n >> 1class Solution {
public int numberOfCuts(int n) {
return n > 1 && n % 2 == 1 ? n : n >> 1;
}
}class Solution {
public:
int numberOfCuts(int n) {
return n > 1 && n % 2 == 1 ? n : n >> 1;
}
};func numberOfCuts(n int) int {
if n > 1 && n%2 == 1 {
return n
}
return n >> 1
}function numberOfCuts(n: number): number {
return n > 1 && n & 1 ? n : n >> 1;
}impl Solution {
pub fn number_of_cuts(n: i32) -> i32 {
if n > 1 && n % 2 == 1 {
return n;
}
n >> 1
}
}public class Solution {
public int NumberOfCuts(int n) {
return n > 1 && n % 2 == 1 ? n : n >> 1;
}
}