pyvkfft - python interface to the CUDA and OpenCL backends of VkFFT (Vulkan Fast Fourier Transform library)

VkFFT is a GPU-accelerated Fast Fourier Transform library for Vulkan/CUDA/HIP/OpenCL.

pyvkfft offers a simple python interface to the CUDA and OpenCL backends of VkFFT, compatible with pyCUDA, CuPy and pyOpenCL.

The documentation can be found at https://pyvkfft.readthedocs.io

Installation

Install using pip install pyvkfft (works on macOS, Linux and Windows). See below for an installation using conda-forge, or for an installation from source.

Notes:

• the PyPI package includes the VkFFT headers and will automatically install pyopencl if opencl is available. However you should manually install either cupy or pycuda to use the cuda backend.
• if you want to specify the backend to be installed (which can be necessary e.g. if you have nvcc installed but cuda is not actually available), you can do that using e.g. VKFFT_BACKEND=opencl pip install pyvkfft. By default the opencl backend is always installed, and the cuda one if nvcc is found.
• If you need to support more than 8 dimensions for the transforms, you can use e.g. VKFFT_MAX_FFT_DIMENSIONS=10 pip install pyvkfft.

Requirements:

• pyopencl and the opencl libraries/development tools for the opencl backend
• pycuda or cupy and CUDA developments tools (nvcc, nvrtc library) for the cuda backend
• numpy
• on Windows, this requires visual studio (c++ tools) and a cuda toolkit installation, with either CUDA_PATH or CUDA_HOME environment variable. However it should be simpler to install using conda, as detailed below
• Optional:
  • scipy and pyfftw for more accurate tests (and to test DCT/DST)

This package can be installed from source using pip install ..

Note: python setup.py install is now disabled, to avoid messed up environments where both methods have been used.

Installation using conda

You can use conda (or much faster mamba) to install pre-compiled binaries with CUDA and OpenCL support on linux-x86_64, linux-aarch64, linux-ppc64le, win-amd64, macos-x86_64, macos-arm64 platforms.

conda config --add channels conda-forge
conda install pyvkfft

Note regarding CUDA support: there are multiple package versions of pyvkfft available, with either only OpenCL support, or compiled using the cuda nvrtc library versions 11.2, 11.8 or 12.x. If you want cuda support, you can install pyvkfft while using the cuda-version meta-package to select a specific cuda version. For example:

# Only install pyvkfft, select cuda nvrtc 11.2
conda install pyvkfft cuda-version=11.2

# Install pyvkfft, pyopencl, cupy with nvrtc version 12
conda install pyvkfft pyopencl cupy cuda-version=12

The only constraint is that the cuda driver must be more recent than the cuda nvrtc version requested installed (type conda info or mamba info to see conda's detected __cuda variable).

See more information in conda-forge's documentation

Once installed, you can use the pyvkfft-info script to see which languages, backends (pyopencl, pycuda, cupy) and GPU devices are available.

Installation from source (git)

git clone --recursive https://github.com/vincefn/pyvkfft.git
cd pyvkfft
pip install .

As indicated above, you can use environmental variables VKFFT_BACKEND and VKFFT_MAX_FFT_DIMENSIONS during the pip install to select the backend or the maximum number of transformed dimensions.

Examples

The simplest way to use pyvkfft is to use the pyvkfft.fft interface, which will automatically create the VkFFTApp (the FFT plans) according to the type of GPU arrays (pycuda, pyopencl or cupy), and also cache these apps:

import pycuda.autoprimaryctx
import pycuda.gpuarray as cua
from pyvkfft.fft import fftn
import numpy as np

d0 = cua.to_gpu(np.random.uniform(0,1,(200,200)).astype(np.complex64))
# This will compute the fft to a new GPU array
d1 = fftn(d0)

# An in-place transform can also be done by specifying the destination
d0 = fftn(d0, d0)

# Or an out-of-place transform to an existing array (the destination array is always returned)
d1 = fftn(d0, d1)

See the scripts and notebooks in the examples directory. An example notebook is also available on google colab. Make sure to select a GPU for the runtime.

Features

• CUDA (using PyCUDA or CuPy) and OpenCL (using PyOpenCL) backends
• complex (C2C) transforms
• R2C/C2R, now fully supporting odd sizes for the fast axis with inplace transforms
• Direct Cosine or Sine transforms (DCT/DST) of type 1, 2, 3 and 4
• out-of-place or inplace
• single and double precision for all transforms (double precision requires device support)
• Allows up to 8 FFT dimensions by default (can be increased by using VKFFT_MAX_FFT_DIMENSIONS when installing).
• arrays can have more dimensions than the FFT (batch transforms).
• Options are available to tune (manually or automatically) the performance for specific GPUs.
• arbitrary array size, using Bluestein algorithm for prime numbers>13 (note that in this case the performance can be significantly lower, up to ~4x, depending on the transform size, see example performance plot below). Now also uses Rader's FFT algorithm for primes from 17 up to max shared memory length (~10000, see VkFFT's doc for details)
• transform along a given list of axes, e.g. using a 4-dimensional array and supplying axes=(-3,-1). For R2C transforms, the fast axis must be transformed.
• normalisation=0 (array L2 norm * array size on each transform) and 1 (the backward transform divides the L2 norm by the array size, so FFT*iFFT restores the original array)
• Support for C (default) and F-ordered arrays, for C2C and R2C transforms
• unit tests for all transforms: see test sub-directory. Note that these take a long time to finish due to the extensive number of sub-tests.
• Note that out-of-place C2R transform currently destroys the complex array for FFT dimensions >=2
• tested on macOS (10.13.6/x86, 12.6/M1), Linux (Debian/Ubuntu, x86-64 and power9), and Windows 10 (Anaconda python 3.8 with Visual Studio 2019 and the CUDA toolkit 11.2)
• GPUs tested: mostly nVidia cards, but also some AMD cards and macOS with M1 GPUs.
• inplace transforms do not require an extra buffer or work area (as in cuFFT), unless the x size is larger than 8192, or if the y and z FFT size are larger than 2048. In that case a buffer of a size equal to the array is necessary. This makes larger FFT transforms possible based on memory requirements (even for R2C !) compared to cuFFT. For example you can compute the 3D FFT for a 1600**3 complex64 array with 32GB of memory.
• transforms can either be done by creating a VkFFTApp (a.k.a. the fft 'plan'), with the selected backend (pyvkfft.cuda for pycuda/cupy or pyvkfft.opencl for pyopencl) or by using the pyvkfft.fft interface with the fftn, ifftn, rfftn and irfftn functions which automatically detect the type of GPU array and cache the corresponding VkFFTApp (see the example notebook pyvkfft-fft.ipynb).
• the pyvkfft-test command-line script allows to test specific transforms against expected accuracy values, for all types of transforms.
• pyvkfft results are evaluated before any release with a comprehensive test suite, comparing transform results for all types of transforms: single and double precision, 1D, 2D and 3D, inplace and out-of-place, different norms, radix and Bluestein, etc... The pyvkfft-test-suite script can be used to run the full suite, which takes more than two days on an A40 GPU using up to 16 parallel process, with about 1.5 million unit tests. Here are the test results for pyvkfft 2024.1:
  • A40 cuda test results
  • H100 opencl test results
  • Apple M1 OpenCL test results

Performance

See the benchmark notebook, which allows to plot OpenCL and CUDA backend throughput, as well as compare with cuFFT (using scikit-cuda) and clFFT (using gpyfft).

The pyvkfft-benchmark script is available to make simple or systematic testss, also allowing to compare with cuFFT and clFFT.

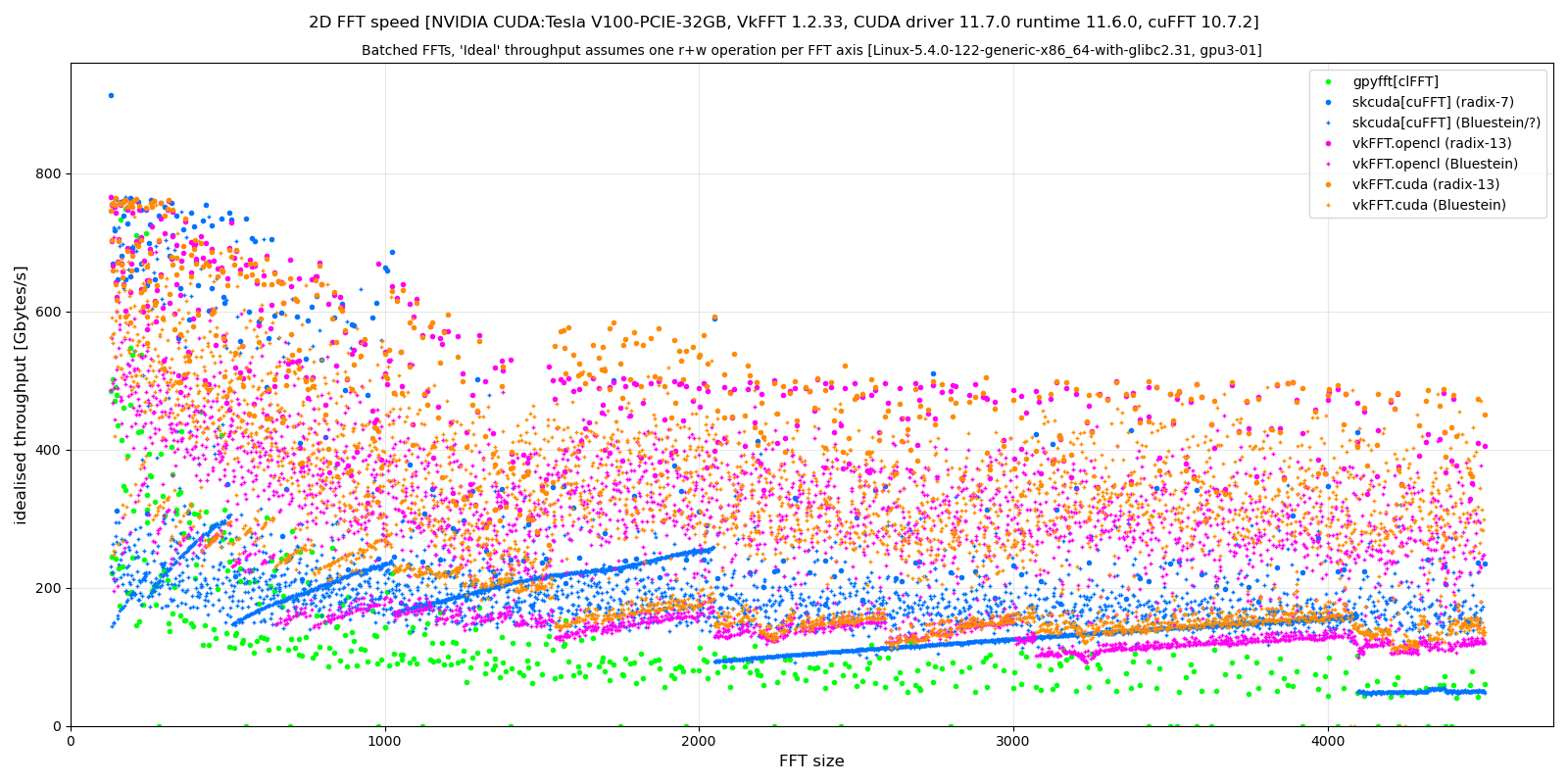
Example results for batched 2D, single precision FFT with array dimensions of batch x N x N using a V100:

Notes regarding this plot:

• the computed throughput is theoretical, as if each transform axis for the couple (FFT, iFFT) required exactly one read and one write. This is obviously not true, and explains the drop after N=1024 for cuFFT and (in a smaller extent) vkFFT.
• the batch size is adapted for each N so the transform takes long enough, in practice the transformed array is at around 600MB. Transforms on small arrays with small batch sizes could produce smaller performances, or better ones when fully cached.

The general results are:

• vkFFT throughput is similar to cuFFT up to N=1024. For N>1024 vkFFT is much more efficient than cuFFT due to the smaller number of read and write per FFT axis (apart from isolated radix-2 3 sizes)
• the OpenCL and CUDA backends of vkFFT perform similarly, though there are ranges where CUDA performs better, due to different cache. [Note that if the card is also used for display, then difference can increase, e.g. for nvidia cards opencl performance is more affected when being used for display than the cuda backend]
• clFFT (via gpyfft) generally performs much worse than the other transforms, though this was tested using nVidia cards. (Note that the clFFT/gpyfft benchmark tries all FFT axis permutations to find the fastest combination)

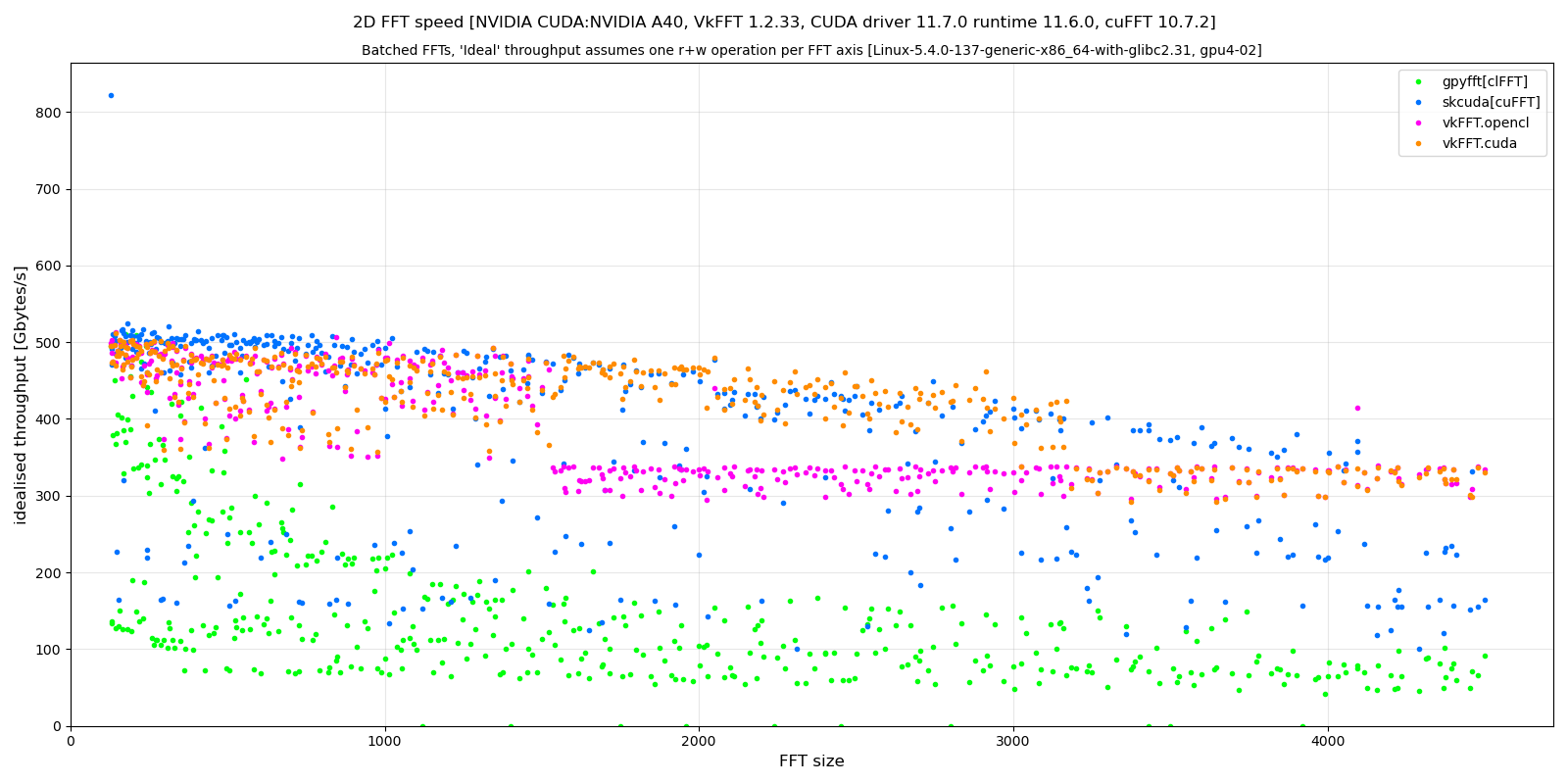
Another example on an A40 card (only with radix<=13 transforms):

On this card the cuFFT is significantly better, even if the 11 and 13 radix transforms supported by vkFFT give globally better results.

Performance tuning

Starting with VkFFT 1.3.0 and pyvkfft 2023.2, it is possible to tweak low-level parameters including coalesced memory or warp size, batch grouping, number of threads, etc...

Optimising those is difficult, so only do it out of curiosity or when trying to get some extra performance. Generally, VkFFT defaults work quite well. Using the simple FFT API, you can activate auto-tuning by passing tuning=True to the transform functions (fftn, rfftn, etc..). Only do this when using iterative process which really require fine-tuning !

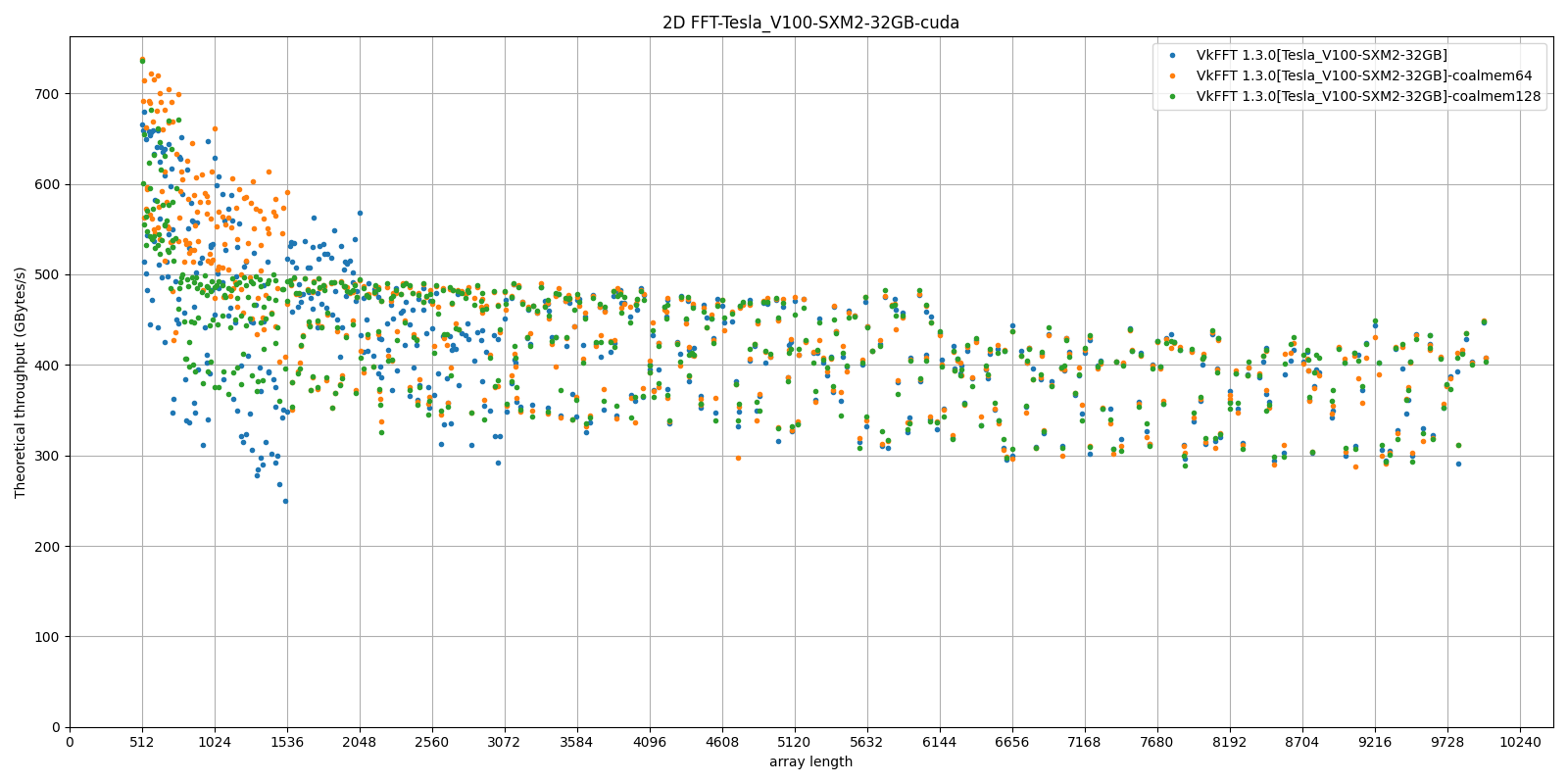
Here is an example of the benchmark ran on a V100 GPU by tuning the coalescedMemory parameter (default value=32):

As you can see the optimal value varies with the 2D array size: below n=1536, using coalescedMemory=64 gives the best results, 32 (default) is best between 1536 and 2048, and above that there is little difference between the values chosen.

The same test on an A40 shows little difference. On an Apple M1 pro, it is the aimThreads parameter which is better tuned from 128 (default) to 64 to yield up to 50% faster transforms. YMMV !

Accuracy

See the accuracy notebook, which allows to compare the accuracy for different FFT libraries (pyvkfft with different options and backend, scikit-cuda (cuFFT), pyfftw), using pyfftw long-double precision as a reference.

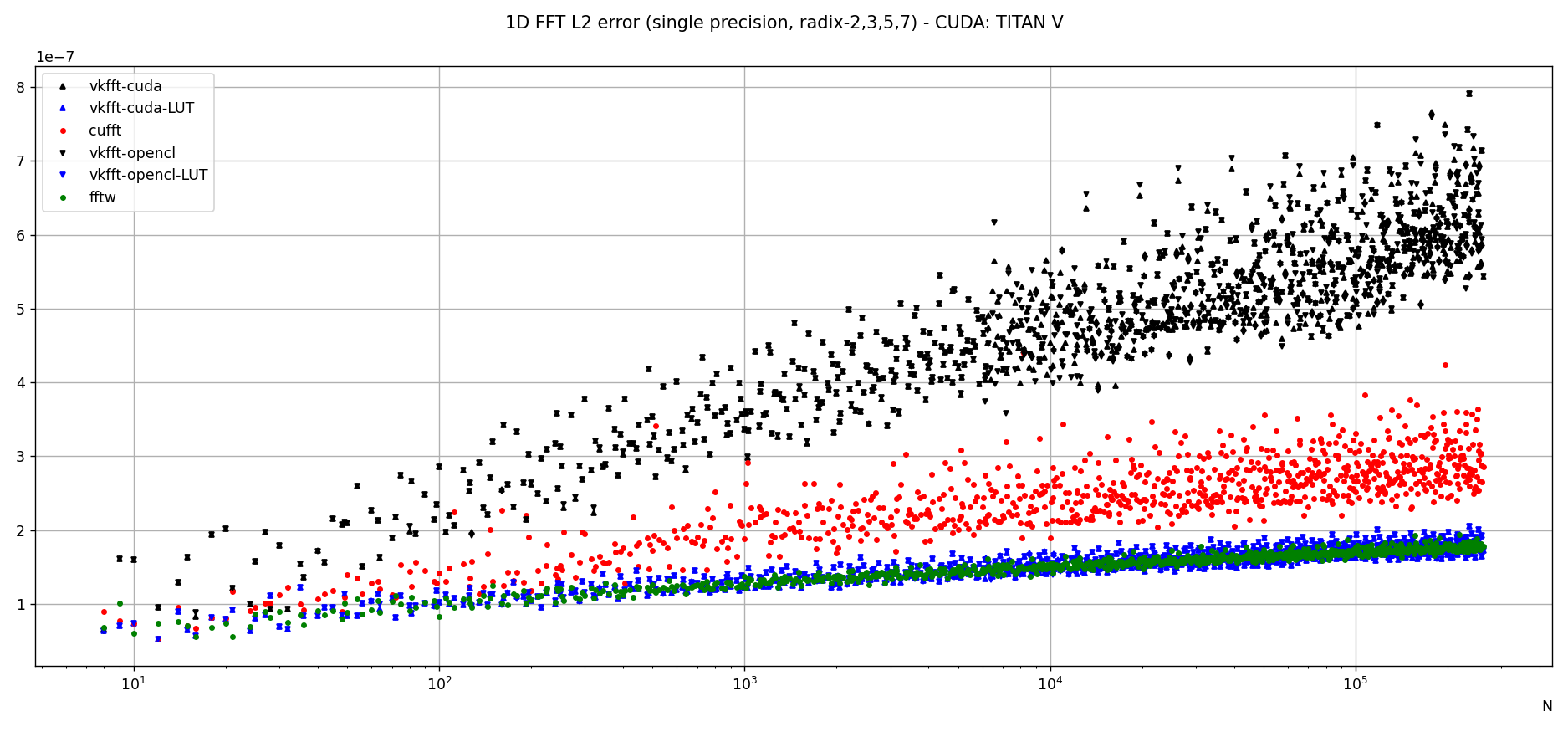
Example results for 1D transforms (radix 2,3,5 and 7) using a Titan V:

Analysis:

• in single precision on the nVidia Titan V card, the VkFFT computed accuracy is about 3 times larger (worse) than pyfftw (also computed in single precision), e.g. 6e-7 vs 2e-7, which can be pretty negligible for most applications. However when using a lookup-table (LUT) for trigonometric values instead of hardware functions (useLUT=1 in VkFFTApp), the accuracy is identical to pyfftw, and better than cuFFT.
• accuracy is the same for cuda and opencl, though this can depend on the card and drivers used (e.g. it's different on a GTX 1080)

You can easily test a transform using the pyvkfft-test command line script, e.g.:

pyvkfft-test --systematic --backend pycuda --nproc 8 --range 2 4500 --radix --ndim 2

Use pyvkfft-test --help to list available options.

You can use the pyvkfft-test-suite script to run the comprehensive test suite which is used to evaluate pyvkfft before a new release. Several options are available to target specific (C2C, R2C..) transforms or even run a random subset of transform sizes for fast detection of issues.

TODO

• access to the other backends:
  • for vulkan and rocm this only makes sense combined to a pycuda/cupy/pyopencl equivalent.
• out-of-place C2R transform without modifying the C array ? This would require using a R array padded with two wolumns, as for the inplace transform
• half precision ?
• on-the-fly convolution ?
• zero-padding ?
• access to the code of the generated kernels ?

Authors & acknowledgements

• Vincent Favre-Nicolin (@vincefn, ESRF-The European Synchrotron) - main pyvkfft author
• Dmitrii Tolmachev, @DTolm - VkFFT author
• Fernando Isuru (@isuruf) - conda package and other contributions