Part 3: populating the world

Step 13: draw monsters on the map

What a monster is? It can be represented by coordinates and a texture id:

struct Sprite {
    float x, y;
    size_t tex_id;
};

[..]

std::vector<Sprite> sprites{ {1.834, 8.765, 0}, {5.323, 5.365, 1}, {4.123, 10.265, 1} };

Having defined few monsters, let us draw them on the map:

You can see the modifications here.

---

Step 14: black squares as a placeholder

Now we will draw sprites in our 3D viewport. For each sprite we need to compute two things: its position on the screen and its size. This function draws a black square on the screen for each sprite:

void draw_sprite(Sprite &sprite, FrameBuffer &fb, Player &player, Texture &tex_sprites) {
    // absolute direction from the player to the sprite (in radians)
    float sprite_dir = atan2(sprite.y - player.y, sprite.x - player.x);
    // remove unnecessary periods from the relative direction
    while (sprite_dir - player.a >  M_PI) sprite_dir -= 2*M_PI; 
    while (sprite_dir - player.a < -M_PI) sprite_dir += 2*M_PI;

    // distance from the player to the sprite
    float sprite_dist = std::sqrt(pow(player.x - sprite.x, 2) + pow(player.y - sprite.y, 2)); 
    size_t sprite_screen_size = std::min(2000, static_cast<int>(fb.h/sprite_dist));
    // do not forget the 3D view takes only a half of the framebuffer, thus fb.w/2 for the screen width
    int h_offset = (sprite_dir - player.a)*(fb.w/2)/(player.fov) + (fb.w/2)/2 - sprite_screen_size/2;
    int v_offset = fb.h/2 - sprite_screen_size/2;

    for (size_t i=0; i<sprite_screen_size; i++) {
        if (h_offset+int(i)<0 || h_offset+i>=fb.w/2) continue;
        for (size_t j=0; j<sprite_screen_size; j++) {
            if (v_offset+int(j)<0 || v_offset+j>=fb.h) continue;
            fb.set_pixel(fb.w/2 + h_offset+i, v_offset+j, pack_color(0,0,0));
        }
    }
}

Let us break it down. First, start with this drawing:

In the very first line of our function we compute the angle sprite_dir. It is an absolute angle, angle between the direction from the player to the sprite and the x axis. The relative angle between the player's gaze direction and the sprite is easy to compute with a simple subtraction: sprite_dir - player.a. The distance from the player to the sprite is trivial to compute, and the sprite screen size can be obtained as a simple division by the distance. I clamped the max sprite size by 2000 pixels, otherwise nothing prevents the squares to be HUGE. By the way, nothing prevents this code to divide by zero. h_offset and v_offset give screen coordinates of the upper left corner of the sprite. To draw the sprite we need a simple double loop.

Take a pencil and check all the computations. By the way, the commit contains an (non-critical) bug; this text is correct. The bug was also fixed in the repository with later commits.

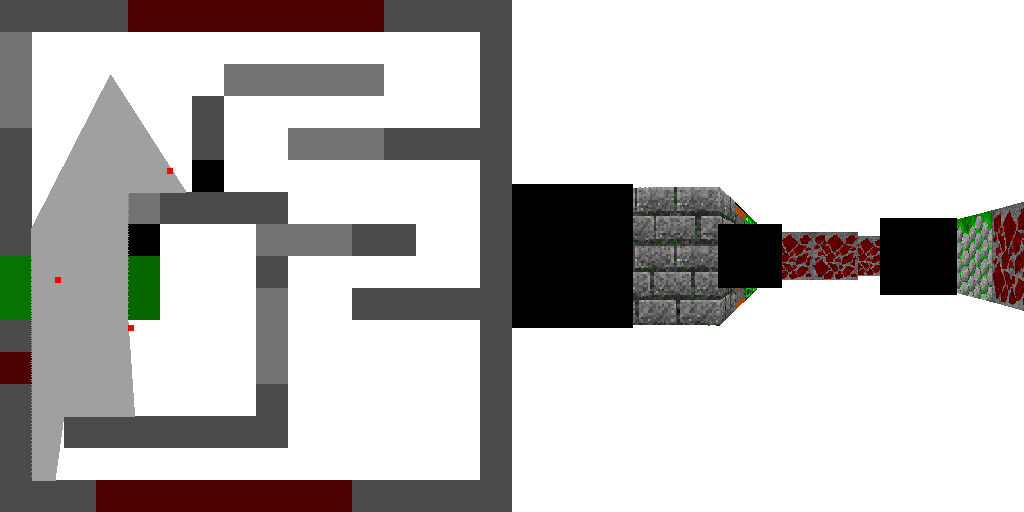
You can see the modifications here.

---

Step 15: depth map

Our squares are exquisite, if not for one problem: the farthest monster hides behind the wall, while the black square is drawn entirely. How to fix that? Very simple. We draw sprites after the walls have been drawn. Therefore, for each column of our screen (each ray casted) we know the distance to the nearest wall. Let's save these distances into an array[512]. Later on, pass this array to the sprite drawing function. Sprites are also drawn column by column, thus for each sprite column we can compare the distance with the depth array.

You can see the modifications here.

---

Step 16: one more problem with the sprites

I love my monsters, but at this step I would not add any new features, I'll break the renders by adding one more monster:

You can see the modifications here.

---

Step 17: sort the sprites

What was the problem? The problem is that we can have an arbitrary order of sprites drawing, and for each of them I compare its distance with the walls, but not with other sprites. So it is only reasonable for the distant creature to show in fron of the closest one. Tell me, is it possible to adapt the depth map approach for sprite drawing?

The answer is yes. How? Think about it.

I'm gonna go the other way, I use the brute force. I'll just paint all the sprites from the farthest to the closest. That is, I will sort the sprites in descending order of distance to the player, and draw them in that order.

You can see the modifications here.