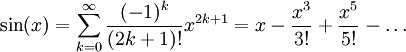Package to add support for pointfree style programming in Python. Specifically this package overloads operators as higher order functions and implements a mechanism for currying.
Pointfree style allows programmers to build new functions out of existing functions without needing to explicitly mention the arguments. It provides a higher level of abstraction, encourages more modular and reusable code, and can often result in more compact, clearer versions of the code. Most importantly though, it can make it easier to reason about code.
Download the latest source from GitHub and run the install script:
python setup.py install
- Python 3.5+
from pfpy import Function, unaryThis is the wrapper class that allows regular unary functions to make use of the higher order function operators. There are two equivalent ways to convert a regular unary function into a Function: using the decorator or using the class constructor.
@unary
def sqr(x):
return x ** 2def add1(x):
return x + 1
add1 = Function(add1)In both cases, the original function name can still be used as you would normally:
sqr(4) # 16
add1(4) # 5Functions allow you to perform arithmetic operations on them to produce a new Function.
Let's say you wanted to write the function f(x) = x2 + x + 1.
Using our functions defined from above and without doing anything special, we could define f as follows:
def f(x):
return sqr(x) + add1(x)
f(4) # 21However, this package allows us to equivalently rewrite that as:
f = sqr + add1
f(4) # 21Notice how sqr + add1 produces a new function which we then call with the argument 4. Also notice how we were able to completely drop the repeated references to x and focus on just the functions themselves.
Let's see some examples without the intermediary function:
(sqr + add1)(4) # sqr(4) + add1(4) = 21
(sqr - add1)(4) # sqr(4) - add1(4) = 11
(sqr * add1)(4) # sqr(4) * add1(4) = 80
(sqr / add1)(4) # sqr(4) / add1(4) = 3.2
(-sqr)(4) # -sqr(4) = -16
(3 * sqr)(4) # 3 * sqr(4) = 48
(add1 ** 2)(4) # add(4) ** 2 == 25This syntax should be extremely familiar to anyone with a background in mathematics.
The following table summarizes the supported arithmetic operators and their corresponding application rewrite rules.
| Operation | Syntax | Application rewrite rule |
|---|---|---|
| Addition | f + g |
f(x) + g(x) |
| Subtraction | f - g |
f(x) - g(x) |
| Multiplication | f * g |
f(x) * g(x) |
| True division | f / g |
f(x) / g(x) |
| Floor division | f // g |
f(x) // g(x) |
| Positive | +f |
+f(x) |
| Negative | -f |
-f(x) |
| Scalar multiplication | c * f |
c * f(x) |
| Exponentiation | f ** c |
f(x) ** c |
Functions also have operators that allow you to combine them through composition, that is, using the output of one function as the input for another. The output of a Function composed with another Function is a new Function.
Let's say we wanted to write the function g(x) = (x + 1)2.
Using our functions defined from above and without doing anything special, we could define g as follows:
def g(x):
return sqr(add1(x))
g(4) # 25However, this package allows us to equivalently rewrite that as:
g = sqr @ add1
g(4) # 25Notice how sqr @ add1 produces a new function which we then call with the argument 4. Also once again notice how we were able to drop the references to x and focus on just the functions that are involved.
Those of you with a mathematics background will hopefully notice how this could have be written in terms of the composition operator ∘. Unfortunately, that isn't a recognized operator in Python. But luckily the @ (matrix multiplication) operator is, and is relatively unused, and looks pretty similar compared to all the other recognized operators.
For some programs, function composition in this order is not a natural way to think about the code. For example, sqr @ add1 forces us to think about the outermost function first. What if we wanted to consider the innermost function first? This is more in line with a data pipeline flow which those of you who have done some command line scripting would be familiar with.
We can equivalently rewrite g to express this semantics:
g = add1 >> sqrt
g(4) # 25Here the repurposed operator is the >> (right shift) operator. It was chosen due to its similarities with the bind operator >>= from Haskell and the composition operator >> from F#.
The following table summarizes the supported composition operators and their corresponding application rewrite rules.
| Syntax | Application rewrite rule |
|---|---|
f @ g |
f(g(x)) |
f >> g |
g(f(x)) |
*These do not change the operator precedence of @ or >>.
from pfpy import Predicate, predicateA predicate is a function that returns True or False. This is the wrapper class that allows regular unary predicates to make use of the higher order operator functions. There are two equivalent ways to convert a regular unary predicate into a Predicate: using the decorator or using the class constructor.
@predicate
def is_even(x):
return x % 2 == 0def is_positive(x):
return x > 0
is_positive = Predicate(is_positive)In both cases, the original predicate name can still be used as you would normally:
is_even(5) # False
is_positive(5) # TruePredicates allow you to perform logical operations on them to produce a new Predicate.
Let's say you wanted to write a function is_even_and_positive that checked if a number was both even and positive.
Using our functions defined from above and without doing anything special, we could define is_even_and_positive as follows:
def is_even_and_positive(x):
return is_even(x) and is_positive(x)
is_even_and_positive(5) # FalseHowever, this package allows us to equivalently rewrite that as:
is_even_and_positive = is_even & is_positive
is_even_and_positive(5) # FalseNotice how is_even & is_positive produces a new function which we then call with the argument 5. Also notice how we were able to completely drop the repeated references to x and focus on just the functions themselves.
Let's see some examples without the intermediary function:
(is_even & is_positive)(5) # is_even(5) and is_positive(5) = False
(is_even | is_positive)(5) # is_even(5) or is_positive(5) = True
(~is_even)(5) # not is_even(5) = TrueThis syntax takes advantage of the bitwise operators &, |, and ~ to express and, or, and not respectively.
The following table summarizes the supported logical operators and their corresponding application rewrite rules.
| Operation | Syntax | Application rewrite rule |
|---|---|---|
| And | f & g |
f(x) and g(x) |
| Or | f | g |
f(x) or g(x) |
| Not | ~f |
not f(x) |
Predicates also support the same composition operators (@, >>, <<) that Functions do. Refer to the relevant section in the section on the Function class for the explanation and summary of these operators. This allows for Predicates and Functions to be composed with one another as necessary. The output of a Predicate composed with a Function is a new Predicate, while the output of a Function composed with a Predicate is a new Function.
from pfpy import curry, rcurry, PredicateSo far we have only been able to work with unary functions. What if we wanted to express functions with more than one arguments? Currying is the act of transforming an n-ary function into a chain of n unary functions.
Let's say we had an add function:
def add(x, y):
return x + y
sub(4, 5) # 9The curried form of this add function would be:
def add(x):
def addx(y):
return x + y
return addx
add(4)(5) # 9Note that with two arguments in the original function, we had to make two function calls on the curried function in order to produce the same result. Also note that the order of function calls corresponds with the order the arguments were originally defined in from left to right. The arguments are incrementally bound with each call.
This package provides two decorators to enable currying.
@curry(n: int[, cls: type]) -> function - Decorator that transforms an n-ary function into a chain of n unary functions that partially applies the arguments of the original function from left to right. Each unary function will be of type Function except for the last one which will be of type cls.
@rcurry(n: int[, cls: type]) -> function - Decorator that transforms an n-ary function into a chain of n unary functions that partially applies the arguments of the original function from right to left. Each unary function will be of type Function except for the last one which will be of type cls.
As an example of usage, we can curry the add function from above:
@curry(2)
def add(x, y):
return x + y
add(4)(5) # 9One benefit of currying is that we can delay evaluation by stopping before the last argument. This allows us to redefine add1 and sqr from above in terms of the curried add and the regular built-in pow:
add1 = add(1)
sqr = rcurry(2)(pow)(2)
add1(4) # 5
sqr(4) # 16Note that rcurry is used for pow since we want to fix the right most argument of pow as 2 in order to give us x2. If we just used curry we would end up with 2x.
For convenience, this package provides the pfpy.curried module which comes with the appropriately curried form of many useful operators and functions. These were drawn from the operator, functools, and itertools modules as well as the built-in functions provided by Python.
The following table summarizes the curried operators and their corresponding application rules.
| Operation | Syntax | Application rule |
|---|---|---|
| Less than | lt(a)(b) |
b < a |
| Less than or equal | le(a)(b) |
b <= a |
| Equality | eq(a)(b) |
b == a |
| Inequality | ne(a)(b) |
b != a |
| Greater than | gt(a)(b) |
b > a |
| Greater than or equal | ge(a)(b) |
b >= a |
| Identical | is_(a)(b) |
b is a |
| Not identical | is_not(a)(b) |
b is not a |
| Containment | contains(a)(b) |
a in b |
| Concatenation | concat(a)(b) |
b + a |
| Subscripting | getitem(a)(b) |
b[a] |
| Count | countOf(a)(b) |
b.count(a) |
| Index | indexOf(a)(b) |
b.index(a) |
| Attribute retrieval | getattr(a)(b) |
b.a |
| Bitwise and | and_(a)(b) |
b & a |
| Bitwise or | or_(a)(b) |
b | a |
| Bitwise exclusive or | xor(a)(b) |
b ^ a |
| Left shift | lshift(a)(b) |
b << a |
| Right shift | rshift(a)(b) |
b >> a |
| Addition | add(a)(b) |
b + a |
| Subtraction | sub(a)(b) |
b - a |
| Multiplication | mul(a)(b) |
b * a |
| True division | truediv(a)(b) |
b / a |
| Floor division | floordiv(a)(b) |
b // a |
| Modulo | mod(a)(b) |
b % a |
| Exponentiation | pow(a)(b) |
b ** a |
| Mapping | map(f)(a) |
map(f, a) |
| Filtering | filter(f)(a) |
filter(f, a) |
| Application | apply(f)(a) |
f(*a) |
| Reduction | reduce(f)(a) |
reduce(f, a) |
| Grouping | groupby(f)(a) |
groupby(a, key=f) |
| Sorting | sorted(f)(a) |
sorted(a, key=f) |
| Maximum | max(f)(a) |
max(a, key=f) |
| Minimum | max(f)(a) |
min(a, key=f) |
from functools import partial
from pfpy import rpartialAnother way to convert an n-ary function into an unary function is through direct partial application. Instead of currying and then incrementally binding, we can directly bind k arguments at once, leaving us with an (n - k)-ary function.
The first function that enables us to do this is partial from the functools module in Python. It binds arguments from the left and can also bind arguments by keyword. Refer to the documentation for more details.
The second function comes from this package:
rpartial(f: function, *args: List[any]) -> function - Return f with arguments bound from the right. Similar to functools.partial but in reverse.
This allows us to redefine sqr from above in terms of the regular built-in pow without needing to curry it first:
sqr = rpartial(pow, 2)
sqr(4) # 16For the binary operators, only one of the operands needs to be a Function or Predicate. The other operand just needs to callable, that is they implement the Callable abstract base class. This allows for greater flexibility in terms of which functions you can use without needing to worry about type. For example, the following expressions will work as expected where abs and bool are both the regular built-in functions:
(abs @ add1)(-4) # 3
(is_even & bool)(0) # Falsefrom pfpy import identity, constantFor the cases where you really need a Function, this package provides two special functions to help you quickly build one.
Function identity(x: any) -> any - Return x.
Function constant(x: any) -> Function - Return an unary function that always returns x.
Using these two functions, we could rewrite add1 and sqr from above as:
add1 = identity + constant(1)
sqr = identity ** 2
add1(4) # 5
sqr(4) # 16When immediately applying a function built using the composition operators >>, the transition between function composition and function call can be disruptive. For example, consider (f >> g >> h)(x). x will get pass in as an argument to the function f, but x is on the side furthest away from f. This motivates the decision to have the >> operator be overloaded to interpret x >> f as f(x) when x is not Callable.
Using our functions defined from above, we can call our functions using the overloaded composition operator:
4 >> add1 # 5
4 >> sqr # 16Note that due to >> being evaluated from left to right, this approach requires all functions in the chain of >> to be either a Function or a Predicate.
The following are some examples of possible applications of this package. They all start from scratch and do not assume that anything has already been defined.
Let's say we wanted to implement our own version of the sine function using its Taylor series.
Immediately we can see that sine is built from the summation of functions where each function consists of a scalar multiplied with an exponential function.
We will use generator comprehension to build the series, and then the sum function to build our version of sine.
from pfpy import identity
from math import factorial
series = ((pow(-1, k) / factorial(2 * k + 1)) * (identity ** (2 * k + 1))
for k in range(20))
my_sin = sum(series)Testing against the sin function from the math module, we get around 14 decimal places of accuracy with diminishing accuracy the further we get from 0.
import math
my_sin(3) # 0.1411200080598671
math.sin(3) # 0.1411200080598672
my_sin(5) # -0.9589242746631358
math.sin(5) # -0.9589242746631385
my_sin(8) # 0.9893582466230959
math.sin(8) # 0.9893582466233818Let's say we had a small JSON dataset of restaurant information, and we imported it into Python as an array of dictionaries.
data = [
{
"name": "Restaurant A",
"location": {
"address": "1 Bloor Street West",
"city": "Toronto",
"province": "Ontario"
},
"is_24_hour": True,
"rating": 5
},
{
"name": "Restaurant B",
"location": {
"address": "1 Yonge Street",
"city": "Toronto",
"province": "Ontario"
},
"is_24_hour": False,
"rating": 3
},
{
"name": "Restaurant C",
"location": {
"address": "1 Robson Street",
"city": "Vancouver",
"province": "British Columbia"
},
"is_24_hour": False,
"rating": 4
}
]Before doing any queries, let's build some getter functions first.
from pfpy import Predicate
from pfpy.curried import getitem
get_name = getitem("name")
get_city = getitem("location") >> getitem("city")
is_24_hour = Predicate(getitem("is_24_hour"))
get_rating = getitem("rating")For our first query, we will find the name of all the restaurants located in Toronto with a rating greater than or equal to 4. We can do this two ways: with list comprehension or without.
from pfpy import curry, Function
from pfpy.curried import filter, map
@curry(2, Predicate)
def is_in(city, restaurant):
return get_city(restaurant) == city
@curry(2, Predicate)
def has_rating_ge(threshold, restaurant):
return get_rating(restaurant) >= threshold
list = Function(list)
[get_name(r)
for r in data
if (is_in("Toronto") & has_rating_ge(4))(r)] # ["Restaurant A"]
(data >> filter(is_in("Toronto") & has_rating_ge(4))
>> map(get_name)
>> list) # ["Restaurant A"]For our second query, we will calculate the average rating of restaurants in each city. Once again, we can do this with list comprehension or without.
from pfpy.curried import sorted, groupby, apply
avg = (Function(sum) / len) @ list
[(k, (avg @ map(get_rating))(g))
for k, g
in (groupby(get_city) @ sorted(get_city))(data)] # [("Toronto", 4.0), ("Vancouver", 4.0)]
(data >> sorted(get_city)
>> groupby(get_city)
>> (map @ apply)(lambda k, g: (k, (avg @ map(get_rating))(g)))
>> list) # [("Toronto", 4.0), ("Vancouver", 4.0)]Note that the initial sorted is necessary due to the way groupby works. Also note that map @ appply is equivalent to starmap.
For our final query, we will get the cities with at least 1 restaurant that's open 24 hours.
[k for k, g
in (groupby(get_city) @ sorted(get_city))(
r for r in data if is_24_hour(r))] # ["Toronto"]
(data >> filter(is_24_hour)
>> sorted(get_city)
>> groupby(get_city)
>> (map @ apply)(lambda k, g: k)
>> list) # ["Toronto"]- This StackOverflow post which gave me the initial idea of overloading operators as higher order functions
- Java 8 functional interfaces for the class names of
FunctionandPredicate - The pointfree package for the idea of using decorators.
- This blog post which I loosely followed to implement my own version of
curry. - The Funcy package for its implementation of
rpartial