Skip to content

liwangshengya/data-structure

BranchesTags

Folders and files

NameName
Last commit message
Last commit date

Latest commit

 

History

287 Commits
img
img
 
 
数据结构程序
数据结构程序
 
 
README.md
README.md
 
 

Repository files navigation

数据结构课笔记

1.链表

学生信息

学生信息管理系统
//============================================================================
// Name        : LinkBlank.cpp
// Author      :
// Version     :
// Copyright   : Your copyright notice
// Description : Hello World in C++, Ansi-style
//============================================================================

#include <stdio.h>
#include<string.h>
#include<malloc.h>
#include<stdlib.h>
#include<stdbool.h>

#define NO_LENGTH  20
#define NAME_LENGTH 11

/* 定义学生结构体的数据结构 */
typedef struct Student {
	char studentNo[NO_LENGTH];
	char studentName[NAME_LENGTH];
}st;

/* 定义每条记录或节点的数据结构 */
typedef struct node
{
	struct Student data; //数据域
	struct node* next; //指针域
}Node, * Link;  //Node为node类型的别名,Link为node类型的指针别名

//定义提示菜单
void myMenu() {
	printf(" * * * * * * * * * 菜     单 * * * * * * * * * *\n");
	printf("     1 增加学生记录            2 删除学生记录                     \n");
	printf("     3 查找学生记录            4 修改学生记录                     \n");
	printf("     5 统计学生人数            6 显示学生记录                     \n");
	printf("     7 退出系统                                     \n");
	printf(" * * * * * * * * * * * * * * * * * * * * * * * *\n");
}

void inputStudent(Link l) {
	printf("请输入学生学号:");
	scanf("%s", l->data.studentNo);
	printf("请输入学生的姓名:");
	scanf("%s", l->data.studentName);

	//每个新创建的节点的next域都初始化为NULL
	l->next = NULL;
}

void inputStudentNo(char s[], char no[]) {
	printf("请输入要%s的学生学号:", s);
	scanf("%s", no);
}

void displayNode(Link head) {
	// 填写代码，根据传入的链表head头指针，扫描链表显示所有节点的信息
	Link p;
	p = head->next;
	while (p!=NULL)
	{
		printf("%s   %s\n", p->data.studentNo,p->data.studentName);
		p = p->next;
	}
}

/* 增加学生记录 */
bool addNode(Link head) {
	Link p, q;   //p,q两个节点一前一后
	Link node;  //node指针指向新创建的节点
	node = (Link)malloc(sizeof(Node));
	inputStudent(node);

	q = head;
	p = head->next;  //q指向head后面的第一个有效节点
	if (head->next == NULL)
		//链表为空时
		head->next = node;
	else {
		//循环访问链表中的所有节点
		while (p != NULL) {
			if (strcmp(node->data.studentNo, p->data.studentNo) < 0) {
				//如果node节点的学号比p节点的学号小，则插在p的前面，完成插入后，提前退出子程序
				q->next = node;
				node->next = p;
				return true;
			}
			else {
				//如果node节点的学号比p节点的学号大，继续向后移动指针（依然保持pq一前一后）
				q = p;
				p = p->next;

			}
		}
		//如果没能提前退出循环，则说明之前没有插入，那么当前node节点的学号是最大值，此时插在链表的最后面
		q->next = node;

	}
	return true;
}

bool deleteNode(Link head) {
	// 按照给定的学号删除学生记录，如果删除成功返回true，如果没找到学号返回false

	//输入要处理的学号
	char no[NO_LENGTH];
	inputStudentNo("删除", no);
	Link p, q;
	p = head->next; q = head;
	if (head == NULL || head->next == NULL) {
		return false;
	}
	while (p != NULL) {
		if (strcmp(no, p->data.studentNo) == 0) {
			q->next = p->next;
			free(p);
			return true;
		}
		else
		{
			q = p;
			p = p->next;
		}
	}
	return false;
}

bool queryNode(Link head) {
	// 按照给定的学号查询学生记录，如果删除成功返回true，如果没找到学号返回false

	//输入要处理的学号
	char no[NO_LENGTH];
	inputStudentNo("查找", no);
	Link p;
	p = head->next;
	while (p != NULL) {
		if (strcmp(p->data.studentNo,no)==0)
		{
			printf("%s   %s\n", p->data.studentNo, p->data.studentName);
			return true;
		}
		else {
			p = p->next;
		}
	}

	return false;
}

bool modifyNode(Link head) {
	// 按照给定的学号找到学生记录节点，如果修改成功返回true，如果没找到学号返回false

	//输入要处理的学号
	void insertStudentNo(Link head, Link node);
	char no[NO_LENGTH];
	char new_no[NO_LENGTH];
	inputStudentNo("修改", no);
	Link p, q;
	p = head->next;
	q = head;
	while (p != NULL) {
		if (strcmp(no, p->data.studentNo) == 0) {
			q->next = p->next;
			p->next = NULL;
			printf("请输入新的学号:\n");
			scanf("%s", new_no);
			strcpy(p->data.studentNo, new_no);
			insertStudentNo(head, p);
			return true;
		}
		else
		{
			q = p;
			p = p->next;
		}
	}

	return false;
}
void insertStudentNo(Link head, Link node)
{
	Link p, q;
	p = head->next; q = head;
	while (p!=NULL)
	{
		if (strcmp(node->data.studentNo,p->data.studentNo)<0) {
			q->next = node;
			node->next = p;
			//return true;
		}
		else {
			q = p;
			p = p->next;
		}
	}
	q->next = node;
	//return true;
}
int countNode(Link head) {
	//统计学生人数，扫描链表统计节点个数，返回节点数
	Link p;
	int count = 0;
	p = head->next;

	//填充代码
	while (p != NULL) {
		count++;
		p = p->next;
	}
	return count;
}

void clearLink(Link head) {
	Link q, p;
	//遍历链表，用free语句删除链表中用malloc建立起的所有的节点
	p = head->next;
	q = head;
	while (p!=NULL) {
		free(q);
		q = p;
		p = p->next;
	}
    free(q);
}
int main() {
	int select;
	int count;
	Link head;  // 定义链表

	//建立head头结点，在这个程序中head指向头结点，头结点data部分没有内容，其后续节点才有真正的数据
	head = (Link)malloc(sizeof(Node));
	head->next = NULL;

	while (1)
	{
		myMenu();
		printf("\n请输入你的选择(0-7):");  //显示提示信息
		scanf("%d", &select);
		switch (select)
		{
		case 1:
			//增加学生记录
			if (addNode(head))
				printf("成功插入一个学生记录。\n\n");
			break;
		case 2:
			//删除学生记录
			if (deleteNode(head))
				printf("成功删除一个学生记录。\n\n");
			else
				printf("没有找到要删除的学生节点。\n\n");
			break;
		case 3:
			//查询学生记录
			if (queryNode(head))
				printf("成功找到学生记录。\n\n");
			else
				printf("没有找到要查询的学生节点。\n\n");
			break;
		case 4:
			//修改学生记录
			if (modifyNode(head))
				printf("成功修改一个学生记录。\n\n");
			else
				printf("没有找到要修改的学生节点。\n\n");
			break;
		case 5:
			//统计学生人数
			count = countNode(head);
			printf("学生人数为：%d\n\n", count);
			break;
		case 6:
			//显示学生记录
			displayNode(head);
			break;
		case 7:
			//退出前清除链表中的所有结点
			clearLink(head);
			return 0;
		default:
			printf("输入不正确，应该输入0-7之间的数。\n\n");
			break;
		}
	}
	return 0;
}
学生成绩管理
#include <stdio.h>
#include<string.h>
#include<malloc.h>
#include<stdlib.h>
#include<stdbool.h>
#define NO_LENGTH 20
#define NAME_LENGTH 11
#define N 3
int count = 0;
/* 定义学生结构体的数据结构 */
typedef struct Student {
	char studentNo[NO_LENGTH];
	char studentName[NAME_LENGTH];
	int Chinese;
	int Math;
	int English;
	int sum;
	int grade;
}st;
/* 定义每条记录或节点的数据结构 */
typedef struct node
{
	struct Student data; //数据域
	struct node* next; //指针域
}Node, * Link;  //Node为node类型的别名,Link为node类型的指针别名
//定义提示菜单
void myMenu() {
	printf(" * * * * * * * * * 菜     单 * * * * * * * * * *\n");
	printf("     1 增加学生记录            2 删除学生记录                     \n");
	printf("     3 查找学生记录            4 修改学生记录                     \n");
	printf("     5 统计学生人数            6 显示学生记录                     \n");
	printf("     7 退出系统                                     \n");
	printf(" * * * * * * * * * * * * * * * * * * * * * * * *\n");
}
void inputStudent(Link l) {
	printf("请输入学生学号:");
	scanf("%s", l->data.studentNo);
	printf("请输入学生的姓名:");
	scanf("%s", l->data.studentName);
	printf("请输入学生的成绩(语文,数学,英语):");
	scanf("%d%d%d",&l->data.Chinese,&l->data.Math,&l->data.English );
	l->data.sum = (l->data.Chinese + l->data.Math + l->data.English);
	//每个新创建的节点的next域都初始化为NULL
	l->next = NULL;
}
void inputStudentNo(char s[], char no[]) {
	printf("请输入要%s的学生学号:", s);
	scanf("%s", no);
}

void display(Node* head)
{
	Node* p;
	p = head->next;
	while (p != NULL)
	{
		printf("%s	%s", p->data.studentNo, p->data.studentName);
		printf("	%d	%d	%d	%d	%d\n",p->data.grade, p->data.Chinese, p->data.Math, p->data.English,p->data.sum);
		p = p->next;
	}
}
bool addNode(Link head)//添加学生记录
{
	Link p, q, node;
	node = (Node*)malloc(sizeof(Node));
	p = head->next;
	q = head;//p q一前一后
	inputStudent(node);
	if (head->next == NULL)
	{
		head->next = node;//链表为空时
		count++;
		node->data.grade = count;
		return true;
	}
	else
	{
		while (p != NULL) {
			if (node->data.sum > p->data.sum)
			{////如果node节点的sum比p节点的sum大，则插在p的前面，完成插入后，提前退出子程序
				q->next = node;
				node->next = p;
				count++;
				node->data.grade = count;
				return true;
			}
			else
			{////如果node节点的sum比p节点的sum小，继续向后移动指针（依然保持pq一前一后）
				q = p;
				p = p->next;
			}
		}
		//如果没能提前退出循环，则说明之前没有插入，那么当前node节点的sum是最小值，此时插在链表的最后面
		q->next = node;
	}
	return true;
}
bool deleteNode(Link head) {
	// 按照给定的学号删除学生记录，如果删除成功返回true，如果没找到学号返回false

	//输入要处理的学号
	char no[NO_LENGTH];
	inputStudentNo("删除", no);
	Link p, q;
	p = head->next;
	q = head;
	if (head == NULL || head->next == NULL)
	{
		return false;//空表
	}
	while (p != NULL)
	{
		if (strcmp(p->data.studentNo, no) == 0)
		{
			q->next = p->next;
			free(p);
			return true;
		}
		else
		{
			q = p;
			p = p->next;
		}
	}
	return false;//循环结束说明没有找到
}

bool queryNode(Link head)
{
	// 按照给定的学号查询学生记录，如果删除成功返回true，如果没找到学号返回false
	Link p;
	p = head->next;
	//输入要处理的学号
	char no[NO_LENGTH];
	inputStudentNo("查询", no);
	while (p!=NULL)
	{
		if (strcmp(p->data.studentNo,no)==0)
		{
			printf("%s   %s", p->data.studentNo, p->data.studentName);
			printf("%d	%d	%d	%d	%d\n", p->data.grade, p->data.Chinese, p->data.Math, p->data.English, p->data.sum);
			return true;
		}
		else
		{
			p = p->next;
		}
	}
	return false;
}
bool modifyNode(Link head) {
	// 按照给定的学号找到学生记录节点，如果修改成功返回true，如果没找到学号返回false

	//输入要处理的学号
	char no[NO_LENGTH];
	//char new_no[NO_LENGTH];
	inputStudentNo("修改", no);
	Link p, q;
	p = head->next; q = head;
	while (p!=NULL)
	{
		if (strcmp(p->data.studentNo,no)==0)
		{
			q = p->next;
			p->next = NULL;
			printf("请重新输入改学生的信息:\n");
			addNode(head);
			return true;
		}
		else
		{
			q = p;
			p = p->next;
		}
	}
	return false;


}

void clearLink(Link head)
{
	Link p;
	while (head!=NULL)
	{
		p = head;
		head = head->next;
		free(p);
	}
}
int main() {
	int select;
	//int count;
	Link head;  // 定义链表

	//建立head头结点，在这个程序中head指向头结点，头结点data部分没有内容，其后续节点才有真正的数据
	head = (Link)malloc(sizeof(Node));
	head->next = NULL;

	while (1)
	{
		myMenu();
		printf("\n请输入你的选择(0-7):");  //显示提示信息
		scanf("%d", &select);
		switch (select)
		{
		case 1:
			//增加学生记录
			if (addNode(head))
				printf("成功插入一个学生记录。\n\n");
			break;
		case 2:
			//删除学生记录
			if (deleteNode(head))
				printf("成功删除一个学生记录。\n\n");
			else
				printf("没有找到要删除的学生节点。\n\n");
			break;
		case 3:
			//查询学生记录
			if (queryNode(head))
				printf("成功找到学生记录。\n\n");
			else
				printf("没有找到要查询的学生节点。\n\n");
			break;
		case 4:
			//修改学生记录
			if (modifyNode(head))
				printf("成功修改一个学生记录。\n\n");
			else
				printf("没有找到要修改的学生节点。\n\n");
			break;
		case 5:
			//统计学生人数
			//count = countNode(head);
			printf("学生人数为：%d\n\n", count);
			break;
		case 6:
			//显示学生记录
			printf("学号	姓名	名次	语文	数学	英语	总分\n");
			display(head);
			break;
		case 7:
			//退出前清除链表中的所有结点
			clearLink(head);
			return 0;
		default:
			printf("输入不正确，应该输入0-7之间的数。\n\n");
			break;
		}
	}
	return 0;
}

约瑟夫环问题

1.循环列表法
#include<stdio.h>
#include<stdlib.h>
typedef struct nodde
{
	int data;
	struct node* next;
}NODE;
int main()
{
	int m, n;//n只猴子数到m退出
	int answer[100];//amswer 用来存放所以的答案
	int count = 0;//count 记录答案
	int i;//计数
	NODE* head, * tail, * p, * q;//p指向当前正在处理的节点,q为p指针指向的前一个节点
	//创建头节点,将其数据域设置为-1
	head = (NODE*)malloc(sizeof(NODE));
	head->data = -1;
	head->next = NULL;

	while (1)
	{
		printf("请输入猴子的总个数n和报数m:\n");
		scanf("%d%d", &n, &m);
		if (m == 0 || n == 0) {
			free(head);
			break;
		}
		else {
			tail = head;
			for (int i = 0; i < n; i++)
			{
				//采用尾插法创建一个循环列表,tail指向最后一个节点
				p = (NODE*)malloc(sizeof(NODE));
				tail->next = p;//插到尾部
				p->data = i + 1;
				p->next = head->next;//最后一个节点next域指向第一个节点,形成循环列表
				tail = p;//tail移动到下一个节点
			}

			p = head->next;
			q = tail;
			i = 1;
			while (q != p) {
				if (i==m)
				{
					q->next = p->next;//吧p节点(出局的猴子)从链表中删除
					free(p);
					p = q->next;//令p指向下一个节点
					i = 1;//重新从1开始计数
				}
				else
				{
					q = p;//p,q各向后边移动一个节点
					p = p->next;
					i++;
				}
			}


			head->next = q;//当仅剩2个节点时,删除前面的节点时会造成链表不完整,头节点不在指向后面的节点
	
			//将答案记录到answer数组中
			answer[count] = p->data;
			count++;
			free(p);
			head->next = NULL;
		

		}
	}

	for (int  i = 0; i < count; i++)
	{
		printf("第%d号猴子为猴王\n", answer[i]);
	}
}
2.数组标志位法
#include<stdio.h>
int main()
{
	int m, n;//n只猴子,报到m
	int number;//记录猴子个数
	int count=1;//报数
	int i, pos;
	while (1)
	{
		printf("请输入猴子的总个数n和报数m:\n");
		scanf("%d%d", &n, &m);
		int monkey[301] = { 0 };//monkey数组存储猴子的编号和状态
		//存储0代表猴子出局
		if (m == 0 || n == 0) {
			break;
		}
		else
		{
		number = n;
		for (int i = 0; i < n; i++)
		{
			monkey[i] = i + 1;
		}
		pos = 0;//pos控制当前处理的数组的下标
		count = 1;
		while (number>1)
		{
			if (monkey[pos]>0)
			{
				if (count == m) {
					monkey[pos] = 0;//标识为0代表猴子出局
					number--;//猴子个数减一
					pos = (pos + 1) % n;//当前处理的数组下标加一,pos向后移动
					count = 1;//重新计数
				}
				else
				{
					count++;
					pos = (pos + 1) % n;//pos向后移动
				}
			}
			else
			{
				pos = (pos + 1) % n;//向后移动
			}
		}
		}
		for (int  i = 0; i < n; i++)
		{
			if (monkey[i] != 0)
				printf("第%d号猴子为猴王\n", monkey[i]);

		}

	}
}
3.数组链表法
#include<stdio.h>
int main()
{
	int m, n;//猴子个数与报数m
	int count;//jishu
	int number;//记录猴子个数
	int i, pos, prior;
	while (1)
	{
		printf("请输入猴子的总个数n和报数m:\n");
		scanf("%d%d", &n, &m);
		int monkey[301] = { 0 };//数组存储下一个猴子的位置,标识为-1的为退出的猴子
		if (m == 0 || n == 0) {
			break;
		}
		else
		{//初始化数组,数组存值为下一个猴子的下标
			for ( i = 0; i < n-1; i++)
			{
				monkey[i] = i + 1;
			}
			monkey[i] = 0;//下标为n-的元素的下个序号为0,形成循环链表
			monkey[i + 1] = -2;//将超过范围的元素标识为-2,方便跟踪时查看数组内存
			count = 1;
			number = n;
			pos = 0;
			prior = n - 1;
			while (number>1)
			{
				if (count==m)
				{
					monkey[prior] = monkey[pos];//更改链接关系
					monkey[pos] = -1;//猴子出局,标识位-1
					pos = monkey[prior];//pos移动到下一个节点
					number--;//猴子数减一
					count = 1;//重新计数
				}
				else
				{
					prior = pos;//prior保存pos的上一个节点的下标
					pos = monkey[pos];//pos移动到下一个有效节点
					count++;
				}
			}
			printf("第%d个猴子是猴王\n",pos+1);
		}
	}
}
4.数学方法(递归)
#include<stdio.h>
int josephus(int n, int m)
{
	if (n == 1)
	{
		return 0;
	}
	else
	{
		return (josephus(n - 1, m) + m) % n;
	}
}
int main()
{
	int m, n;
	scanf("%d%d", &n, &m);
	int s;
	s = josephus(n, m) + 1;
	printf("%d", s);
}
#include<stdio.h>
int main()
{
	int m, n, i;
	scanf("%d%d", &n, &m);
	int s = 0;
	//s = josephus(n, m) + 1;
	for ( i = 0; i <=n; i++)
	{
		s = (s + m) % n;
	}
	printf("%d", s+1);
}

多项式问题

1.多项式的输出(一修修补补)

描述

一元 n 次多项式可用如下的表达式表示：

f(x)=anxn+an-1xn-1+...+a1x+a0，an≠0

其中，aixi称为i次项，ai称为i次项的系数。给出一个一元多项式各项的次数和系数，请按照如下规定的格式要求输出该多项式：

  1. 多项式中自变量为x，从左到右按照次数递减顺序给出多项式。
  2. 多项式中只包含系数不为0的项。
  3. 如果多项式n次项系数为正，则多项式开头不出现“+”号，如果多项式n次项系数为负，则多项式以“-”号开头。
  4. 对于不是最高次的项，以“+”号或者“-”号连接此项与前一项，分别表示此项系数为正或者系数为负。紧跟一个正整数，表示此项系数的绝对值（如果一个高于0次的项，其系数的绝对值为1，则无需输出1）。如果x的指数大于1，则接下来紧跟的指数部分的形式为“x^b”，其中b为x的指数；如果x的指数为1，则接下来紧跟的指数部分形式为“x”； 如果x的指数为0，则仅需输出系数即可。
  5. 多项式中，多项式的开头、结尾不含多余的空格。

输入

共有2 行： 第一行 1 个整数 n，表示一元多项式的次数。 第二行有 n+1 个整数，其中第 i 个整数表示第 n-i+1 次项的系数，每两个整数之间用空格隔开。

1 ≤ n ≤ 100，多项式各次项系数的绝对值均不超过100。

输出

共1行，按题目所述格式输出多项式。

样例输入

样例 #1：
5
100 -1 1 -3 0 10

样例 #2：
3
-50 0 0 1

样例输出

样例 #1：
100x^5-x^4+x^3-3x^2+10

样例 #2：
-50x^3+1

代码示例:

#include<stdio.h>
#include<stdlib.h>
typedef struct node
{
	int coef;//系数
	int expn;//指数
	struct node* next;//指针域
}NODE;
int main()
{
	NODE* head, *tail, * p;
	int n, i;
	int a[101];
	scanf("%d", &n);
	/*for ( i = 0; i <=n; i++)
	{
		scanf("%d", &a[i]);
	}*/
	head = (NODE*)malloc(sizeof(NODE));
	head->next = NULL;
	tail = head;
	for ( i = 0; i <= n; i++)//尾插法创建多项式列表
	{
		scanf("%d", &a[i]);
		p = (NODE*)malloc(sizeof(NODE));
		p->coef = a[i];
		p->expn = n - i;
		p->next = NULL;
		tail->next = p;
		tail = p;
	}
	tail->next = NULL;
	p = head->next;
	if (p->coef != 0) {
		if (p->coef == 1)printf("x^%d", p->expn);
		else if (p->coef == -1)printf("-x^%d", p->expn);//系数为1或-1时进行特殊处理
		else  printf("%dx^%d", p->coef, p->expn);
	}
	//printf("%dx^%d", p->coef, p->expn);
	p = p->next;
	while (p!=NULL)
	{
	
		if (p->coef>0)
		{
			printf("+");//当系数为正数时输出其前面的"+"号
		}
		if (p->coef==0)
		{
			p = p->next;
			continue;
		}
		if (p->expn != 1 && p->expn != 0) {
			if(p->coef==1)printf("x^%d", p->expn);
			else if(p->coef==-1)printf("-x^%d", p->expn);//系数为1或-1时进行特殊处理
			else printf("%dx^%d", p->coef, p->expn);
		}
		else if (p->expn == 1)//指数为1时进行特殊处理
		{
			if (p->coef == 1)printf("x");
			else if (p->coef == -1)printf("-x");//系数为1或-1时进行特殊处理
			else printf("%dx", p->coef);
		}
		else
		{
			printf("%d", p->coef);
		}
		p = p->next;//令p指向下一个节点
	}
}

2.多项式的输出(二flags判断)

![img](file:///C:\Users\付宇\AppData\Local\Temp\ksohtml21184\wps1.png)![img](file:///C:\Users\付宇\AppData\Local\Temp\ksohtml21184\wps2.png)![img](file:///C:\Users\付宇\AppData\Local\Temp\ksohtml21184\wps3.png)![img](file:///C:\Users\付宇\AppData\Local\Temp\ksohtml21184\wps4.png)-4x^2

flag1 flag2 flag3 flag4

变量 含义 值
flag1 代表是否输出+- 0不输出,1输出-,2输出+
flag2 代表是否输出系数 0不输出,1输出
falg3 代表是否输出x 0不输出,1输出
flag4 代表是否输出^和指数 0不输出,1输出

示例代码:

#include<stdio.h>
#include<stdlib.h>
typedef struct node
{
	int coef;//系数
	int expn;//指数
	struct node* next;//指针域
}NODE;
void printfAsflags(int coef, int expn, int flag1, int flag2, int flag3, int flag4) {
	if (flag1==1)
	{
		printf("-");
	}
	else if (flag1==2)
	{
		printf("+");
	}
	if (flag2 == 1)
	{
		printf("%d", coef);
	}
	if (flag3==1)
	{
		printf("x");
	}
	if (flag4 == 1)
	{
		printf("^%d", expn);
	}
}
void clearLink(NODE* head)
{
	NODE* p, * q;
	p = head->next; q = head;
	while (p!=NULL)
	{
		q = p;
		p = p->next;
		free(q);
	}
	head = NULL;
}
int main()
{
	NODE* head, * tail, * p;
	int n, i;
	int flag1, flag2, flag3, flag4;
	int first;//判断是不是第一项
	head = (NODE*)malloc(sizeof(NODE));
	head->next = NULL;
	tail = head;
	//while (scanf("%d", &n) != EOF)//ctrl+c结束输入
	while(1)
	{
		scanf("%d", &n);
		if (n == 0)break;
		for (i = 0; i <= n; i++)//尾插法创建多项式列表
		{
			p = (NODE*)malloc(sizeof(NODE));
			scanf("%d", &p->coef);
			p->expn = n - i;
			p->next = NULL;
			tail->next = p;
			tail = p;
		}
		tail->next = NULL;

		first = 1;
		p = head->next;
		while (p != NULL)
		{
			//给flag1赋值,判断是否要输出+-
			if (first)//第一项不需要输出+
			{
				if (p->coef > 0)
				{
					flag1 = 0;
					first = 0;
				}
				else if (p->coef < 0)
				{
					flag1 = 1;
					first = 0;
				}
				else
				{
					flag1 = 0;
					first = 1;
				}
			}
			else//不是第一项
			{
				if (p->coef > 0)//系数为正数,输出+
				{
					flag1 = 2;
				}
				else if (p->coef < 0)//系数为负数,输出-
				{
					flag1 = 1;
				}
				else//系数为0不需要输出
				{
					flag1 = 0;
				}
			}
			//给flag2赋值,判断是否需要输出系数
			if (p->coef == 0 || (abs(p->coef) == 1 && p->expn != 0))
			{
				//如果系数为0或(1或-1,且不是最后的常数项)
				flag2 = 0;
			}
			else
			{
				flag2 = 1;
			}
			//给flag3赋值,判断是否需要输出x
			if (p->expn == 0)//指数为0,不需要输出
			{
				flag3 = 0;
			}
			else
			{
				flag3 = 1;
			}
			//给flag4赋值
			if (p->expn == 1 || p->expn == 0)
			{
				flag4 = 0;
			}
			else
			{
				flag4 = 1;
			}
			//对于系数为0的情况都不需要输出
			if (p->coef == 0)
			{
				flag1 = flag2 = flag3 = flag4 = 0;
			}
			//调用函数,根据flag情况输出当前项
			printfAsflags(abs(p->coef), p->expn, flag1, flag2, flag3, flag4);
			//p指向后一位
			p = p->next;
		}
		clearLink(head);
	}
}

3.多项式的加法

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#include<stdbool.h>
#include<string.h>
typedef struct polynomial
{
    int coefficient;//系数
    int exp;//指数
    struct polynomial* next;
}*Link, Node;

void inputPoly(Link head);//用于从控制台读入链表的函数
void print(Link head);//打印链表用的函数
bool insert(Link head, int coefficient, int exp);//向链表插入一个元素的函数
void combin2List(Link heada, Link headb, Link headab);//合并两个链表
void clearLink(Node* head);

int main()
{
    Link headA, headB;//两个多项式的头指针
    Link headAB;//合并后的多项式的头指针

    /*链表的初始化*/
    headA = (Link)malloc(sizeof(Node));
    headA->next = NULL;
    headB = (Link)malloc(sizeof(Node));
    headB->next = NULL;
    headAB = (Link)malloc(sizeof(Node));
    headAB->next = NULL;

    printf("请输入第一个多项式的系数和指数，以(0 0)结束：\n");
    inputPoly(headA);
    printf("第一个");
    print(headA);
    printf("请输入第二个多项式的系数和指数，以(0 0)结束：\n");
    inputPoly(headB);
    printf("第二个");
    print(headB);

    combin2List(headA, headB, headAB);
    printf("合并后");
    print(headAB);
  
    clearLink(headA);
    clearLink(headB);
    clearLink(headAB);
    return 0;
}

/**输入二项式数据的函数*/
/*这个函数用来输入二项式，给用户合适的提示，读入用户输入的系数和指数。
调用函数insert，将用户输入的二项式的一项插入到链表中去。*/
void inputPoly(Link head)
{
    int coefficient, exp;//系数和指数
    printf("请输入系数和指数(如：\"2 3\"表示2x^3)：");
    scanf("%d %d", &coefficient, &exp);
    while (coefficient != 0 || exp != 0)//连续输入多个系数和指数
    {
        insert(head, coefficient, exp);//调函数输入多项式
        printf("请输入系数和指数：");
        scanf("%d %d", &coefficient, &exp);
    }
}

/**向多项式链表中插入元素的函数
int coefficient 一个多项式项的系数
int exp 一个多项式项的幂
*/
bool insert(Link head, int coefficient, int exp)
{
    Link node;  //node指针指向新创建的节点
    Link q, p;   //q,p两个节点一前一后
    p = head->next;
    q = head;
    node = (Node*)malloc(sizeof(Node));
    node->coefficient = coefficient;
    node->exp = exp;
    node->next = NULL;
    //创建一个新结点
    //.....

    if (head->next == NULL)//空表,插第1个
    {
        head->next = node; //......
    }
    else
    {
        while (p!=NULL) { //循环访问链表中的所有节点

            if (node->exp > p->exp) //如果node节点的指数比p节点的指数大，则插在p的前面，完成插入后，提前退出
            {
                node->next = q->next;
                q->next = node;
                return true;

            }
            if (node->exp==p->exp)
            {
                p->coefficient = p->coefficient + node->coefficient;
                free(node);
                return true;
            }  //如果node节点的指数和p节点的指数相等，则合并这个多项式节点，提前退出
            if (node->exp < p->exp)//如果node节点的指数比p节点的指数小，继续向后移动指针（依然保持p，q一前一后）
            {
                q = p;
                p = p->next;
            }
        }
        q->next = node;//如果退出循环是当前指针p移动到链表结尾，则说明之前没有插入，那么当前node节点的指数值是最大值，此时插在链表的最后面
    }
    return true;
}

/**
打印多项式链表的函数
*/
/*
①　通过指针访问链表
②　多重条件语句嵌套
③　数字转换为字符串函数itoa
④　标志是否为第一个节点的flag的设置
⑤　字符串连接函数strcat
⑥　字符串清空函数memset。memset(item,0,20);清空长20的字符串item
请补充代码实现。
*/
void print(Link head)
{
    Link p; //指向链表要输出的结点
    printf("多项式如下：\n");
    p = head->next;

    if (p == NULL)
    {
        printf("多项式为空\n");
        return;
    }
    // 不是空表
    char item[20] = "";//要打印的当前多项式的一项
    char number[7] = "";//暂时存放系数转换成的字符串

    bool isFirstItem = true;//标志是否为第一个节点的flag
    //打印节点
    do {
        memset(item, 0, 20);//清空字符串item
        if (p->coefficient == 0)//如果系数为0直接跳过
        {
            p = p->next;
            continue;
        }
        //如果是第一项，不要打+号
        if (isFirstItem)
        {
          
        }
      
        //如果不是第一项，且系数为正数，要打加号
        else
        {
            if(p->coefficient>0)
            strcat(item, "+");
            //如果系数为负数，系数自身带有符号  
        }


        //如果系数为1，不用打系数
        if (p->coefficient==-1)
        {
            strcat(item, "-");
        }
        //系数为-1打印负号
        //如果系数不为1或-1，打印系数
        else if (p->coefficient!=1 && p->coefficient!=-1 &&p->coefficient!=0)
        {
            itoa(p->coefficient, number, 10);
            strcat(item, number);
        }

        //如果指数为0，直接打系数不用打x^和指数
        //如果系数是-1或1，需要打1出来，不能只打符号
        if (p->exp==0)
        {
            if (p->coefficient == 1 || p->coefficient == -1)
            {
                memset(number, 0, 7);
                itoa(abs(p->coefficient), number, 10);
                strcat(item, number);
            }
        }
        else
        {
            if(p->coefficient!=0)//系数不为0
            strcat(item, "x");//指数不为0
        //打印x
        }

        if (p->exp!=1 &&p->exp!=0 &&p->coefficient!=0)
        {
            memset(number, 0, 7);
            itoa(p->exp, number, 10);
            strcat(item, "^");
            strcat(item, number);
        }
        //如果指数为1，不打指数，否则打指数

        printf("%s", item);//打印当前节点代表的项
        p = p->next;//指向下个结点
        isFirstItem = false;//flag标志不是第一项了
    } while (p != NULL);
    printf("\n");
    return;
}

/**
合并两个有序链表a，b到链表ab
heada.headb,headab分别为链表a,b,ab的头指针
*/
void combin2List(Link heada, Link headb, Link headab)
{
    Link pa, pb;//指向a，b链表和ab的指针
    pa = heada->next;
    pb = headb->next;

    while (pa != NULL && pb != NULL)//a,b链表都没有没有访问完毕
    {
        //如果指数a>指数b，a节点插入ab链表，a指针后移
        if (pa->exp > pb->exp)
        {
            insert(headab, pa->coefficient, pa->exp);
            pa = pa->next;
        }
        //如果指数a<指数b，b节点插入ab链表，b指针后移
        else if (pa->exp<pb->exp)
        {
            insert(headab, pb->coefficient, pb->exp);
            pb = pb->next;

        }
        //如果指数a==指数b，a、b系数相加，插入ab链表，a、b指针后移
        //......
        else
        {
            insert(headab, pa->coefficient + pb->coefficient, pa->exp);
            pa = pa->next;
            pb = pb->next;
        }

    }
    //如果a、b链表还有尾巴，将它加到ab链表后面
    while (pa != NULL)
    {
        insert(headab, pa->coefficient, pa->exp);
        pa = pa->next;
    }
    while (pb != NULL)
    {
        insert(headab, pb->coefficient, pb->exp);
        pb = pb->next;
    }
    return;

}

void clearLink(Node* head)//释放链表
{
    Node* p;
    while (head!=NULL)
    {
        p = head;
        head = head->next;
        free(p);
    }
}

注:在vs中使用itoa()函数进行编译时,会产生如下报错信息,"'itoa': The POSIX name for this item is deprecated. Instead, use the ISO C and C++ conformant name: _itoa. See online help for details."该报错信息为“POSIX命名方式不推荐使用，推荐使用ISO C和C++的函数名itoa”。就是说，itoa()是采用POSIX方式命名的，而_itoa()是采用ISO C方式命名的。

1 产生原因 1.1 POSIX POSIX的全称是Protable Operating System Interface of UNIX，即可移植操作系统接口。POSIX详细描述了一些函数，这些函数是在C标准库之外定义的，这些函数只能被部分的编译器所支持。

1.2 ANSI C ANSI的全称是American National Standards Institute即美国国家标准协会。ANSI C则是ANSI对C语言发布的标准。使用C的软件开发者被鼓励遵循ANSI C文档的要求，因为它鼓励使用跨平台的代码。

ANSIC现在被几乎所有广泛使用的编译器支持。现在多数C代码是在ANSI C基础上写的。任何仅仅使用标准C并且没有任何硬件依赖假设的代码实际上能保证在任何平台上用遵循C标准的编译器编译成功。

1.3 不使用POSIX 从VC++2005文档中提到，微软不再支持传统的POSIX方式命名的C语言函数，取而代之的是在其函数名前加入下划线的函数名，即ANSI C方式命名的函数。 ———————————————— 版权声明：本文为CSDN博主「棉猴」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。 原文链接：https://blog.csdn.net/hou09tian/article/details/80616155

解决方案:

1.使用ANSI C方式命名的函数来替代POSIX方式命名的函数.

2.编译预处理加入"_CRT_NONSTDC_NO_DEPRECATE"和"_CRT_SECURE_NO_WARNINGS".

2.栈和队列

1.堆栈(顺序栈)

预习题

题目:了解堆栈的主要操作,定义堆栈类,并实现主要成员函数:入栈push,出栈pop,堆栈是否为空isEmpty,堆栈是否已满isFull,在实现时只需输出一条标示语句即可,不用实现具体逻辑.写一个main函数并调用这些成员函数

示例:(指针表示)

#include<iostream>
using namespace std;
#define MAXSIZE 1
typedef struct data//数据区
{
	int a;
	int b;
}Node;
Node input(Node* p)
{
	p = new Node;
	p->a = 1;
	p->b = 2;
	return *p;
}
class Stack
{
public:
	Stack();
	~Stack();
	bool Push(Node p);//入栈
	Node Pop(Node p);//出栈
	bool isEmpty();//是否空栈
	bool isFull();//是否栈满

private:
	Node data;
	Node* base, * pop;
	int maxsize;
};

Stack::Stack()//无参构造函数,初始化顺序栈
{
	base = new Node[MAXSIZE];
	pop = base;
	maxsize = MAXSIZE;
}

Stack::~Stack()//析构函数,释放栈
{
	delete[]base;
}
bool Stack::Push(Node p)
{
	if (pop - base == maxsize) return false;
	*pop++ = p;
	cout << "入栈成功" << endl;
	return true;
}
Node Stack::Pop(Node p)
{
	if (pop == base) { cout << "是空栈" << endl;; exit(-1); }
	else
	{
		p = *--pop;
		cout << "出栈成功" << endl;
		return p;
	}
}
bool Stack::isEmpty()
{
	if (base==pop)
	{
		cout << "空栈" << endl;
		return true;
	}
	else
	{
		cout << "不是空栈" << endl;
		return false;
	}
}
bool Stack::isFull()
{
	if (pop-base==maxsize)
	{
		cout << "栈满" << endl;
		return true;
	}
	else
	{
		cout << "不是man栈" << endl;
		return false;
	}
}


int main()
{
	Stack st;
	Node* p;
	p = NULL;
	st.Push(input(p));
	st.Pop(input(p));
	st.isEmpty();
	st.Push(input(p));
	st.isFull();
}

示例(数组表示):

#include<iostream>
using namespace std;
const int MAX_SIZE = 100;
class Stack//
{
public:
	Stack();
	Stack(int s);
	~Stack();
	void push(char ch);//入栈
	char pop();//出栈
	char getTop();//获得栈顶元素
	bool isEmpty();
	bool isFull();
	void setNull();

private:
	char* data;//属性:线性表
	int size;//属性:堆栈的实际大小
	int top;//属性:栈顶
};

Stack::Stack()
{
	size = MAX_SIZE;
	top = -1;
	data = new char[size];//缺省构造函数分配最大内存
}
Stack::Stack(int s)
{
	size = s;
	top = -1;
	data = new char[size];//根据指定的大小分配栈的内存空间
}

Stack::~Stack()
{
	delete []data;//内存回收
}
void Stack::push(char ch)
{
	//if (top == size - 1) exit(-1);//栈满
    if (!isFull()) exit(-1);//栈满
    //判断条件直接用isFull函数来写比较好
	data[++top] = ch;
	cout << "入栈成功" << endl;
}
char Stack::pop()
{
	char ch;
	if (top == -1) exit(-1);//空栈\
    //此处判断条件也应用函数
	ch = data[top--];
	cout << "出栈成功" << ch << endl;
}
char Stack::getTop()
{
	char ch;
	if (top == -1) exit(-1);//空栈
	ch = data[top];
	cout << "栈顶元素为:" << ch << endl;
}
bool Stack::isEmpty()
{
	if (top==-1)
	{
		cout << "空栈" << endl;
		return true;
	}
	else
	{
		cout << "不是空栈" << endl;
		return false;
	}
}
bool Stack::isFull()
{
	if (top == size-1)
	{
		cout << "栈满" << endl;
		return true;
	}
	else
	{
		cout << "为满栈" << endl;
		return false;
	}
}
void Stack::setNull()
{
	top = -1;
}
int main()
{
	Stack st(2);
	st.push('a');
	st.getTop();
	st.isEmpty();
	st.isFull();
	st.pop();
	st.push('a');
	st.push('b');
	st.getTop();
	st.push('c');
	st.getTop();
	st.isEmpty();
	st.setNull();
}
作业二(zifuch处理程序)

在Stack类的基础上,实现一个字符串处理程序.

【题目要求】输入若干串字符,每次遇到换行符n时,则输出 本行当前处理结果。输入时以"#"字符作为结束符,当遇到这个 符号后,意味着字符串输入结束。 在输入过程中如果输入"<",则表示回退一格;在输入过程中如 果包含了"@"则表示回退到本行行首。

示例代码:

#include<stdio.h>
#include<iostream>
using namespace std;
const int MAX_SIZE = 100;
class Stack//
{
public:
	Stack();
	Stack(int s);
	~Stack();
	void push(char ch);//入栈
	char pop();//出栈
	char getTop();//获得栈顶元素
	bool isEmpty();
	bool isFull();
	void setNull();
	void reversedisplay();

private:
	char* data;//属性:线性表
	int size;//属性:堆栈的实际大小
	int top;//属性:栈顶
};

Stack::Stack()
{
	size = MAX_SIZE;
	top = -1;
	data = new char[size];//缺省构造函数分配最大内存
}
Stack::Stack(int s)
{
	size = s;
	top = -1;
	data = new char[size];//根据指定的大小分配栈的内存空间
}

Stack::~Stack()
{
	delete[]data;//内存回收
}
void Stack::push(char ch)
{
	if (top == size - 1) exit(-1);//栈满
	data[++top] = ch;
	//cout << "入栈成功" << endl;
}
char Stack::pop()
{
	char ch;
	if (top == -1) cout << "空栈" << endl; //exit(-1);//空栈
	ch = data[top--];
	return ch;

	//cout << "出栈成功" << ch << endl;
}
char Stack::getTop()
{
	char ch;
	if (top == -1) exit(-1);//空栈
	ch = data[top];
	cout << "栈顶元素为:" << ch << endl;
}
bool Stack::isEmpty()
{
	if (top == -1)
	{
		cout << "空栈" << endl;
		return true;
	}
	else
	{
		cout << "不是空栈" << endl;
		return false;
	}
}
bool Stack::isFull()
{
	if (top == size - 1)
	{
		cout << "栈满" << endl;
		return true;
	}
	else
	{
		cout << "不是满栈" << endl;
		return false;
	}
}
void Stack::setNull()
{
	top = -1;
}
void Stack::reversedisplay()
{
	int i = 0;
	for ( i = 0; i <=top ; i++)
	{
		printf("%c", data[i]);
	}
	printf("\n");
}
int main()
{
	int size;
	char ch;
	printf("请输入栈的大小:\n");
	scanf("%d", &size);
	Stack st(size);
	printf("输入待处理的字符串(输入<代表退一格,输入@代表清楚到行首,输入#结束)\n");
	while (ch=getchar())
	{
		switch (ch)
		{
		case '<':st.pop(); break;
		case '@':st.setNull(); break;
		case'\n':st.reversedisplay(); st.setNull(); break;
		case'#':st.reversedisplay(); st.setNull(); return 0;
		default:
			st.push(ch);
			break;
		}
	}
}

注:cin会屏蔽换行符,故此处不用cin来输入字符串

作业三(回文串)

利用 Stack类判断一个字符串是否为回文串。

【提示】回文字符串是一种关于字符串中心对称的特殊字符串, 如果将字符串从中间划分为两个字符串,则只需要将其中一个字 符串逆序,其结果与另外一个字符串是相等的。显然,回文字符 串的判断中一个重要的操作是将字符串逆序,该操作可以利用栈 的LIFO特性轻松实现。

#include<iostream>
using namespace std;
const int MAX_SIZE = 100;
class Stack//
{
public:
	Stack();
	Stack(int s);
	~Stack();
	void push(char ch);//入栈
	char pop();//出栈
	char getTop();//获得栈顶元素
	bool isEmpty();
	bool isFull();
	void setNull();

private:
	char* data;//属性:线性表
	int size;//属性:堆栈的实际大小
	int top;//属性:栈顶
};

Stack::Stack()
{
	size = MAX_SIZE;
	top = -1;
	data = new char[size];//缺省构造函数分配最大内存
}
Stack::Stack(int s)
{
	size = s;
	top = -1;
	data = new char[size];//根据指定的大小分配栈的内存空间
}

Stack::~Stack()
{
	delete[]data;//内存回收
}
void Stack::push(char ch)
{
	if (top == size - 1) exit(-1);//栈满
	data[++top] = ch;
	//cout << "入栈成功" << endl;
}
char Stack::pop()
{
	char ch;
	if (top == -1) exit(-1);//空栈
	ch = data[top--];
	//cout << "出栈成功" << ch << endl;
}
char Stack::getTop()
{
	char ch;
	if (top == -1) exit(-1);//空栈
	ch = data[top];
	//cout << "栈顶元素为:" << ch << endl;
	return ch;
}
bool Stack::isEmpty()
{
	if (top == -1)
	{
		cout << "空栈" << endl;
		return true;
	}
	else
	{
		cout << "不是空栈" << endl;
		return false;
	}
}
bool Stack::isFull()
{
	if (top == size - 1)
	{
		cout << "栈满" << endl;
		return true;
	}
	else
	{
		cout << "不是满栈" << endl;
		return false;
	}
}
void Stack::setNull()
{
	top = -1;
}
void split(Stack &st,char str[], int n)//将字符串前半部分入栈
{
	int i;
	for ( i = 0; i < n; i++)
	{
		st.push(str[i]);
	}
}
int jiou(int n)//判断奇偶
{
	if (n % 2 != 0) return 1;
	else return 0;
}
int main()
{
	char str[201];
	int count = 0;
	int n;
	Stack st;
	cout << "请输入要检验的字符串:" << endl;
	cin >> str;
	n = strlen(str);
	split(st, str, n/2);
	for ( int i = 0; i <n/2; i++)
	{
		if (st.getTop()==str[n/2+jiou(n)+i])
		{

			count++;
			st.pop();
		}
	}
	if (count==n/2)
	{
		cout << "该字符串是回文串" << endl;
	}
	else
	{
		cout << "该字符串不是回文串" << endl;
	}
	return 0;


}
用异常捕获优化顺序栈

在类的成员函数中包含输出输入语句,应为这不符合类的重用原则.

C++异常处理

try...catch

try{语句1

语句2

语句3

...

}

catch(异常类型){

异常处理代码

}

...

catch(异常类型){

异常处理代码

}

示例代码:

//stacktry.h
#pragma once
#define MAX_SIZE 100
class Stacktry
{
private:
	char* data;//属性:线性表
	int size;//属性:堆栈的实际大小
	int top;//属性:栈顶

public:
	Stacktry();
	Stacktry(int s);
	~Stacktry();
	void push(char ch);//入栈
	char pop();//出栈
	char getTop();//获得栈顶元素
	bool isEmpty();
	bool isFull();
	void setNull();
	class Full{};
	class Empty{};//
};


//stacktry.cpp
#include "Stacktry.h"
Stacktry::Stacktry()
{
	size = MAX_SIZE;
	top = -1;
	data = new char[size];//缺省构造函数分配最大内存
}
Stacktry::Stacktry(int s)
{
	size = s;
	top = -1;
	data = new char[size];//根据指定的大小分配栈的内存空间
}

Stacktry::~Stacktry()
{
	delete[]data;//内存回收
}
void Stacktry::push(char ch)
{
	if (isFull()) {
		throw Full();//丢出异常对象
	}
	else
	{
		data[++top] = ch;
	}
}
char Stacktry::pop()
{
	if (isEmpty())
	{
		throw Empty();
	}
	else
	{
		return data[top--];
	}
}
char Stacktry::getTop()
{
	if (!isEmpty())
	{
		return data[top];
	}
}
bool Stacktry::isEmpty()
{
	if (top == -1)
	{
	
		return true;
	}
	else
	{
	
		return false;
	}
}
bool Stacktry::isFull()
{
	if (top == size - 1)
	{
	
		return true;
	}
	else
	{
	
		return false;
	}
}
void Stacktry::setNull()
{
	top = -1;
}
//main.cpp
#include"Stacktry.h"
#include<iostream>
using namespace std;
int main()
{
	Stacktry s1(2);
	char ch;
	try
	{
		s1.push('a');
		s1.push('b');
		s1.push('c');

	}
	catch (Stacktry::Full)
	{
		cout << "stack Full" << endl;
	}
	try
	{
		ch = s1.pop();
		cout << ch << endl;
		ch = s1.pop();
		cout << ch << endl;
		ch = s1.pop();
		cout << ch << endl;
	}
	catch (Stacktry::Empty)
	{
		cout << "stack Empty" << endl;
	}


	//放在一起捕获到full的异常后就会停止运行程序
	/*try
	{
		s1.push('a');
		s1.push('b');
		s1.push('c');
		ch = s1.pop();
		cout << ch << endl;
		ch = s1.pop();
		cout << ch << endl;
		ch = s1.pop();
		cout << ch << endl;

	}
	catch (Stacktry::Full)
	{
		cout << "stack Full" << endl;
	}
	catch (Stacktry::Empty)
	{
		cout << "stack Empty" << endl;
	}*/
}
用类模板实现顺序栈

类模板是用于设计结构和成员函数完全相同,但所处理的数据类型不同的通用类

c++类模板分文件编写存在的问题 - LoveMee - 博客园 (cnblogs.com)

将类的cpp文件后缀改为.hpp

//.h
#pragma once
const int MAX_SIZE = 100;
template<class DataType>
class Stackmode
{
private:
	DataType* data;//属性:线性表
	int size;//属性:堆栈的实际大小
	int top;//属性:栈顶

public:
	Stackmode();
	Stackmode(int s);
	~Stackmode();
	void push(DataType ch);//入栈
	DataType pop();//出栈
	DataType getTop();//获得栈顶元素
	bool isEmpty();
	bool isFull();
	void setNull();
	class Full {};
	class Empty {};//
};
//为保证模板类可以在其他cpp文件中使用
//需要在源文件的末尾显示的实例化想要用的版本(如int,char)
//相当于为每个类型的模板定义了一个类型
//typedef Stackmode<char> Charstack;
//typedef Stackmode<int> Intstack;
//typedef Stackmode<double> Doublestack;


//.hpp
#include "Stackmode.h"
template<class DataType>
Stackmode<DataType>::Stackmode()
{
	size = MAX_SIZE;
	top = -1;
	data = new char[size];//缺省构造函数分配最大内存
}
template<class DataType>
Stackmode<DataType>::Stackmode(int s)
{
	size = s;
	top = -1;
	data = new char[size];//根据指定的大小分配栈的内存空间
}
template<class DataType>
Stackmode<DataType>::~Stackmode()
{
	delete[]data;//内存回收
}
template<class DataType>
void Stackmode<DataType>::push(DataType ch)
{
	if (isFull()) {
		throw Full();//丢出异常对象
	}
	else
	{
		data[++top] = ch;
	}
}
template<class DataType>
DataType Stackmode<DataType>::pop()
{
	if (isEmpty())
	{
		throw Empty();
	}
	else
	{
		return data[top--];
	}
}
template<class DataType>
DataType Stackmode<DataType>::getTop()
{
	if (!isEmpty())
	{
		return data[top];
	}
}
template<class DataType>
bool Stackmode<DataType>::isEmpty()
{
	if (top == -1)
	{

		return true;
	}
	else
	{

		return false;
	}
}
template<class DataType>
bool Stackmode<DataType>::isFull()
{
	if (top == size - 1)
	{

		return true;
	}
	else
	{

		return false;
	}
}
template<class DataType>
void Stackmode<DataType>::setNull()
{
	top = -1;
}
//在.cpp文件中显示的声明
//template class Stackmode<char>;
//template class Stackmode<int>;
//template class Stackmode<double>;
//main.c
#include"Stackmode.hpp"
#include<iostream>
using namespace std;
int main()
{
	Stackmode<char> s1;
	char ch;
	s1.push('a');
	s1.push('b');
	ch = s1.pop();
	cout << ch << endl;
	ch = s1.pop();
	cout << ch << endl;
	return 0;
}
双端堆栈

用一个数组来存储两个栈,让一个栈的栈底为数组的始端,另一个栈为数组的终端.两个栈从各自的栈底向中间延申.

有点:空间利用率高

//.h
#pragma once
const int STACK_SIZE = 100;
class BothStack
{
private:
	//char data[STACK_SIZE];
	char* data;
	int top1, top2;
public:
	BothStack();
	~BothStack();
	void push(int num, char ch);
	char pop(int num);
	char gettop(int num);
	bool isEmpty(int mun);
	bool isFull();
	void setFull(int num);
	class Full{};
	class Empty{};
};


//.cpp
#include "BothStack.h"
BothStack::BothStack()
{
	data = new char[STACK_SIZE];
	top1 = -1;
	top2 = STACK_SIZE;
}
BothStack::~BothStack()
{

}
void BothStack::push(int num, char ch)
{
	if (isFull())
	{
		throw Full();
	}
	else
	{
		if (num == 1)
		{
			data[++top1] = ch;
		}
		if (num == 2)
		{
			data[--top2] = ch;
		}
	}
}
char BothStack::pop(int num)
{
	if (num == 1) {
		if (isEmpty(1)) throw Empty();
		else return data[top1--];
	}
	if (num == 2) {
		if (isEmpty(2)) throw Empty();
		else return data[top2++];
	}
}
char BothStack::gettop(int num)
{
	if (num == 1) {
		if (isEmpty(1)) throw Empty();
		else return data[top1];
	}
	if (num == 2) {
		if (isEmpty(2)) throw Empty();
		else return data[top2];
	}
}
bool BothStack::isFull()
{
	if (top2 == top1 + 1)
	{
		return true;
	}
	else return false;
}
bool BothStack::isEmpty(int num)
{
	if (num == 1) {
		if (top1 == -1) return true;
		else return false;
	}
	if (num == 2)
	{
		if (top2 == STACK_SIZE) return true;
		else return false;
	}
}
void BothStack::setFull(int num)
{
	if (num == 1) top1 == -1;
	if (num == 2) top2 == STACK_SIZE;
}
//main.c#include"BothStack.h"
#include<iostream>
using namespace std;
int main()
{
	BothStack bs;
	/*bs.push(1, 'a');
	bs.push(1, 'b');
	cout << bs.gettop(1) << endl;
	bs.push(2, 'w');
	bs.push(2, 'q');
	bs.pop(1);
	cout << bs.gettop(1) << endl;
	bs.pop(1);
	bs.pop(1);*/
	try
	{
		bs.push(1, 'a');
		bs.push(1, 'b');
		bs.push(2, 'w');
		bs.push(2, 'q');
	}
	catch (BothStack::Full)
	{
		cout << "Stack Full" << endl;
	}
	try
	{
		cout << bs.gettop(2) << endl;
		bs.pop(2);
		cout << bs.gettop(2) << endl;
		bs.pop(2);
		//cout << bs.gettop(1) << endl;
		bs.pop(2);
		//cout << bs.gettop(1) << endl;
	}
	catch (BothStack::Empty)
	{
		cout << "Stack Empty" << endl;
	}
}

2.链栈

顺序栈和链栈的比较

时间性能:相同,都是常数时间O(1)

空间性能:

顺序栈:有元素个数的限制和空间浪费的问题。

链栈:没有栈满的问题,只有当内存没有可用空 间时才会出现栈满,但是每个元素都需要一个指针 域,从而产生了结构性开销。

总之,当栈的使用过程中元素个数变化较大时,用

//.h
#include<iostream>
#pragma once
typedef struct node {
	char data;
	struct node * next;
}Node;
class LinkStack
{
private:
	Node* top;
public:
	LinkStack();
	~LinkStack();
	void push(char s);
	char pop();
	char getpop();
	bool isEmpty();
	class Empty{};
};


//.cpp
#include "LinkStack.h"
LinkStack::LinkStack()
{
	top = NULL;
}
LinkStack::~LinkStack()
{
	Node* p;
	while (top != NULL)
	{
		p = top;
		top = top->next;
		delete p;
	}
}
void LinkStack::push(char s)
{
	Node* p;
	p = new Node;
	p->next = top;
	p->data = s;
	top = p;
}
char LinkStack::pop()
{
	if (isEmpty()) throw Empty();
	else
	{
		Node* p;
		char x;
		p = top;
		x = p->data;
		top = top->next;
		delete p;
		return  x;
	}
}
char LinkStack::getpop()
{
	if (isEmpty()) throw Empty();
	else
	{
		return top->data;
	}
}
bool LinkStack::isEmpty()
{
	if (top == NULL) return true;
	else return false;
}

3.堆栈应用

1.表达式求值

(3+4)*2

步骤 OPTR栈 OPND栈 读入字符 操作
1 # ( push(OPTR,'(')
2 #( 3 push(OPND,'3')
3 #( 3 + push(OPTR,+)
4 #(+ 3 4 push(OPND,4)
5 #(+ 3 4 ) push(OPND,operate(3+4))
6 #( 7 ) pop(OPTR)
7 # 7 * push(OPTR,'*')
8 #* 7 2 push(OPND,2)
9 #* 7 2 # push(OPND,operate(2*7))
10 # 14 # return gettop(OPND) 
#include"Stackmode.hpp"
#include<iostream>
using namespace std;
bool isOpnd(char ch);//判断是否是操作数
bool isOptr(char ch);//判断是否是运算符
char Precede(char theta1, char theta2);//运算符优先级表
double getch(char ch);//将操作数由字符转换为double
double operate(double a, char theta, double b);//运算
int main()
{
	Stackmode<double>  opnd;//操作数栈
	Stackmode<char>  optr;//运算符栈
	opnd.setNull();
	optr.setNull();
	optr.push('#');
	char ch;
	ch = getchar();
	while (ch!='#' || optr.getTop()!='#')
	{
		if (isOpnd(ch)) { opnd.push(getch(ch)); ch = getchar(); }
		else
		{
			switch (Precede(optr.getTop(),ch))
			{
			case'<':
				optr.push(ch);
				ch = getchar();
				break;
			case'=':
				if (ch == ')') optr.pop();
				ch = getchar();
				break;
			case'>':
				opnd.push(operate(opnd.pop(), optr.pop(), opnd.pop()));
			default:
				break;
			}
		}
	}
	cout << opnd.pop() << endl;
}

bool isOpnd(char ch)
{
	if (ch >= 48 && ch <= 57) return true;
	else return false;
}
bool isOptr(char ch)
{
	const int N = 7;
	char optr[N] = { '+','-' , '*', '/', '(', ')', '#' };
	for (int  i = 0; i < N; i++)
	{
		if (ch == optr[i])  return true; 
	}
	return false;
}
char Precede(char theta1, char theta2)
{
	switch (theta1)
	{
	case'+':
		if (theta2 == '*' || theta2 == '/' || theta2 == '(') return '<';
		else return '>';
	case'-':
		if (theta2 == '*' || theta2 == '/' || theta2 == '(') return '<';
		else return '>';
	case'*':
		if (theta2 == '(') return '<';
		else return '>';
	case'/':
		if (theta2 == '(') return '<';
		else return '>';
	case'(':
		if (theta2 == ')' && theta2 != '#') return '=';
		else return '<';
	case')':
		if (theta2 != '(') return '>';
	case'#':
		if (theta2 != ')' && theta2 == '#') return '=';
		else return '<';
	default:
		break;
	}
}

double getch(char ch)
{
	return double(ch - '0');
}
double operate(double a, char theta, double b)
{
	switch (theta)
	{
	case'+':
		return a + b;
	case'-':
			return a - b;
	case'*':
		return a * b;
	case'/':
		return a / b;
	default:
		break;
	}
}

多位整数

#include"Stackmode.hpp"
#include<iostream>
using namespace std;
bool isOpnd(char ch);//判断是否是操作数
bool isOptr(char ch);//判断是否是运算符
char Precede(char theta1, char theta2);//运算符优先级表
double getch(char ch);//将操作数由字符转换为double
double getS(char s[]);
double operate(double a, char theta, double b);//运算
int main()
{
	Stackmode<double>  opnd;//操作数栈
	Stackmode<char>  optr;//运算符栈
	opnd.setNull();
	optr.setNull();
	optr.push('#');
	char ch;
	char s[10];//临时存放多位数
	int i = 0;
	ch = getchar();
	while (ch != '#' || optr.getTop() != '#')
	{
		while ((!isOptr(ch)) || ch=='.')
		{
			s[i++] = ch;
			ch = getchar();
		}
		if (i != 0) {//i=0时,s为空应排除
			//cout << i << endl;
			cout << getS(s) << endl;
			opnd.push(getS(s));//将操作数入栈
			memset(s, 0, 10);//清空字符串
			i=0;
		}
		switch (Precede(optr.getTop(), ch))
			{
			case'<':
				optr.push(ch);
				ch = getchar();
				break;
			case'=':
				if (ch == ')') optr.pop();
				ch = getchar();
				break;
			case'>':
				opnd.push(operate(opnd.pop(), optr.pop(), opnd.pop()));
			default:
				break;
			
		}
	}
	cout << opnd.pop() << endl;
}

bool isOpnd(char ch)
{
	if (ch >= 48 && ch <= 57) return true;
	else return false;
}
bool isOptr(char ch)//是否为运算符
{
	const int N = 7;
	char optr[N] = { '+','-' , '*', '/', '(', ')', '#' };
	for (int i = 0; i < N; i++)
	{
		if (ch == optr[i])  return true;
	}
	return false;
}
char Precede(char theta1, char theta2)//优先级表
{
	switch (theta1)
	{
	case'+':
		if (theta2 == '*' || theta2 == '/' || theta2 == '(') return '<';
		else return '>';
	case'-':
		if (theta2 == '*' || theta2 == '/' || theta2 == '(') return '<';
		else return '>';
	case'*':
		if (theta2 == '(') return '<';
		else return '>';
	case'/':
		if (theta2 == '(') return '<';
		else return '>';
	case'(':
		if (theta2 == ')' && theta2 != '#') return '=';
		else return '<';
	case')':
		if (theta2 != '(') return '>';
	case'#':
		if (theta2 != ')' && theta2 == '#') return '=';
		else return '<';
	default:
		break;
	}
}

double getch(char ch)
{
	return double(ch - '0');
}

double getS(char s[])//将字符串转换为float类型
{
	return strtod(s, NULL);
}
double operate(double a, char theta, double b)//运算函数
{
	switch (theta)
	{
	case'+':
		return a + b;
	case'-':
		return a - b;
	case'*':
		return a * b;
	case'/':
		return a / b;
	default:
		break;
	}
}
2.迷宫问题(DFS)
#include"Stack.h"
#include <iostream>
using namespace std;
const int M = 8;
const int N = 8;
typedef struct {
	int intcx, intcy;
}Direction;
Direction direct[4] = { {0,1},{1,0},{0,-1},{-1,0} };
bool findPath(int maze[M + 2][N + 2], Direction direct[], Stack& s);
int main()
{
	Stack s;
    int maze[M + 2][N + 2] = {
		{1,1,1,1,1,1,1,1,1,1},
		{1,0,0,1,0,0,0,1,0,1},
		{1,0,0,1,0,0,0,1,0,1},
		{1,0,0,0,0,1,1,0,0,1},
		{1,0,1,1,1,0,0,0,0,1},
		{1,0,0,0,1,0,0,0,0,1},
		{1,0,1,0,0,0,1,0,0,1},
		{1,0,1,1,1,0,1,1,0,1},
		{1,1,0,0,0,0,0,0,0,1},
		{1,1,1,1,1,1,1,1,1,1}
    };
	if (findPath(maze, direct, s)) 
	{	cout << "Find Path" << endl;
		s.display();
		cout << "(" << M<< "," << N<< ")" << endl;
	}
	else cout << "No Path" << endl;
}
bool findPath(int maze[M + 2][N + 2], Direction direct[], Stack& s)
{
	Box temp;
	int x, y, di;//迷宫格子当前的从横坐标和方向
	int line, col;//迷宫数组下一单元的行坐标和列坐标
	maze[1][1] = -1;
	temp = { 1,1,-1 };
	s.push(temp);
	while (!s.isEmpty())
	{
		temp = s.pop();
		x = temp.x; y = temp.y; di = temp.di + 1;
		while (di < 4)
		{
			line = x + direct[di].intcx;
			col = y + direct[di].intcy;
			if (maze[line][col] == 0)
			{
				temp = { x,y,di };
				s.push(temp);
				x = line; y = col;
				maze[line][col] = -1;
				if (x == M && y == N) return true;
				else di = 0;
			}
			else di++;
		}
	}
	return false;
}
3.汉诺塔
#include<iostream>
using namespace std;
void hanoi(int n,char x,char y,char z);
void move(char x,char y);
int main()
{
		int n;
		//char a,b,c;
		cout<<"请输入盘子个数:"<<endl;
		cin>>n;
		hanoi(n,'a','b','c');
}
void hanoi(int n,char x,char y,char z)
//n个盘子由X经y移动到z上
{
	if(n==1) move(x,z);
	else
	{
		hanoi(n-1,x,z,y);
		move(x,z);
		hanoi(n-1,y,x,z);
	}
}
void move(char x,char y)
{
	cout<<x<<"->"<<y<<endl;
}
4.八皇后问题
#include<iostream>
using namespace std;
int number=0;
int place[8]={0};//第n个皇后所占领的列号
	bool flag[8]={true,true,true,true,true,true,true,true};
	//标志数组,表示第col列是否可占,1表示不冲突
	bool d1[15]={true,true,true,true,true,true,true,true,true,true,true,true,true,true,true};
	//表示上对角线是否可占
	bool d2[15]={true,true,true,true,true,true,true,true,true,true,true,true,true,true,true};
	//表示下对角线是否可占
	void generate(int n);
	void print();
int main()
{
	generate(0);
	return 0;
}
void generate(int n)
{
	int col;
	for(col=0;col<8;col++){
		if(flag[col]&&d1[n-col+7]&&d2[n+col]){//判断位置是否冲突
			place[n]=col;//在n行col列摆放皇后
			flag[col]=false;//占领col列
			d1[n-col+7]=false;//占领对角线
			d2[n+col]=false;
			if(n<7) generate(n+1);
			else print();
		
			flag[col]=true;//回溯
			d1[n-col+7]=true;
			d2[n+col]=true;
		
		}
	}
}
void print()
{

	int i,j;
	number++;
	cout<<"No."<<number<<":"<<endl;
	for(i=0;i<8;i++)
	{
		for(j=0;j<8;j++)
		{
			if(j==place[i]) cout<<1<<" ";
			else cout<<0<<" ";
		}
		cout<<endl;
	}
}

4队列

如何确定不同的队空、队满的判定条件? 为什么要将队空和队满的判定条件分开?

方法一:附设一个存储队列中元素个数的变量num,当 num=0时队空,当num=QueueSize时为队满;

方法二:修改队满条件,浪费一个元素空间,队满时数组 中只有一个空闲单元;

方法三:设置标志flag,当 front-rear且flag=0时为队空,当 frontrear且flag=1时为队满。

//.h
#pragma once
#include<iostream>
using namespace std;
const int MAXQSIZE = 6;
class Queue
{
private:char* data;//指定队列存储空间
	   int front;//队首下标
	   int rear;//队尾下表
	   int msize;//存放队列的数组的大小
public:
	Queue();//建立缺省长度(MAXQSIZE)的队列
	Queue(int s);//建立长度位size的队列
	~Queue();//清空队列,释放内存
	bool enQueue(char ch);//入队
	bool deQueue(char &ch);//出队
	bool getQueue(char &ch);//读取对头元素
	bool isEmpty();//判断队列是否为空
	bool isFull();//判断队列是否为满
	void clearQueue();//清空队列
	void displayQueue();//显示队列内容
	int queueLength();//获取队列元素个数
};
#include "Queue.h"
Queue::Queue()
{
	msize = MAXQSIZE;
	data = new char[msize];
	front = rear = 0;
}
Queue::Queue(int s)
{
	msize = s;
	data = new char[msize];
	front = rear = 0;
}
Queue::~Queue()
{
	delete[]data;
}
bool Queue::enQueue(char ch)
{
	if (isFull()) return false;
	else
	{
		data[rear] = ch;
		rear = (rear + 1) % MAXQSIZE;
		return true;
	}
}
bool Queue::deQueue(char &ch)
{

	if (isEmpty()) return false;
	else
	{
		ch = data[front];
		front = (front + 1) % MAXQSIZE;
		return true;
	}
}
bool Queue::getQueue(char& ch)
{
	if (isFull()) return false;
	else
	{
		ch = data[front];
		return true;
	}
}
bool Queue::isEmpty()
{
	if (front == rear) return true;
	else return false;
}
bool Queue::isFull()
{
	if ((rear + 1) % MAXQSIZE == front) return true;
	else return false;
}
void Queue::clearQueue()
{
	rear = front;
}
void Queue::displayQueue()
{
	int i;
	for ( i =(front+msize)%msize; i <(rear+msize)%msize; i++)
	{
		cout << data[i] << endl;
	}
}
int  Queue::queueLength()
{
	return (rear - front + msize) % msize;
}

3.串

1.BF算法(暴力算法Brute Force)

匹配模式T

算法基本思想:

1.在串S和T中这比较的起始下标i和j

2.循环直到S或T的所有字符均未比较玩

2.1.如果是S[i]=T[j],继续比较S和T的下一个字符

2.2 否则,将i和j回溯,准备比较下一趟
  1. 如果T中所有字符均比较完,则匹配成功,返回匹配的其实比较下标;否则,匹配失败,返回-1;
int BF(char S[], char T[])
{
	int i, j;
	i = 0; j = 0;
	while (S[i]!='\0'&& T[j]!='\0')//等同于while(S&&T)
	{
		if (S[i] == T[j])
		{
			i++;
			j++;
		}
		else
		{
			i = i - j + 1;
			j = 0;//若不匹配则对i进行回溯
		}
	}
	if (T[j] == '\0') return i - j;
	else return -1;
}

BF效率

设串S长度为n,串T长度为m,在匹配成功的情况下,考虑两种极端清

最好情况:不成功的匹配都发生在串T的第一个字符.

例如 S="aaaaaaaaaabcdccccc";

T="bcd".

社匹配成功发生在Si处,则在i-1躺不成功的匹配中共匹配了i-

次,第i躺成功的匹配共比较了m次,所以总共比较了i-1+m次,所有匹配成功的可能情况共有n-m+1种

$$ \sum_{i=1}^{n-m+1}{p_i(i-1+m)}=\frac{m+n}{2}=O(m+n ) $$

做坏的情况:不成功的匹配都发生在串T的最后一个字符

例如:S="0000000000000000000000000000001"

T="00001"

模式前4个字符均为"0",主串前40个字符均为"0",每趟比较都在模式的最后一个字符出现不等,此时需要指针回溯到i-3的位置上,并从模式的第一个字符串开始重新比较,整个匹配过程中指针i需要回溯36(40-4)次,则循环次数为37*5,可见算法最坏的平均复杂度为O(nm)

2.KMP算法

伪代码描述:

1.在串S和串T中分别设比较的其实下标i和j

2.循环直到s[i]或t[j]的所有字符均比较玩

2.1如果s[i]和t[j],继续比较s和t的下一个字符

2.2 否则将j向右划动到next[j]位置,即j=next[j]

2.3如果j==-1,则将i和j分别加1,准备下一趟比较

3.如果t中所有字符串军比较完毕,则返回匹配的起始下标,否则返回-1;

int KMP(char s[], char t[], int next[])
{
	int i = 0, j = 0;
	int lens = strlen(s);
	int lent = strlen(t);
		//这里不能用s[i]!='\0'&&t[j]!='\0 来作为结束条件
	 //应为j的值可能等于-1,数组可能会越界
		////这里不能用s[i]!='\0'&&t[j]!='\0 来作为结束条件
	//应为j的值可能等于-1,数组可能会越界
	//while (S[i]!='\0'&& T[j]!='\0')
	//while (i!=lens&&j!=lent)
	while (i< lens && j < lent)
	{
		if (j==-1 || s[i] == t[j]) 
		{
			i++; j++;
		}
		else
		{
			j = next[j];
		}
	}
	//cout << i << "    " << j << endl;
	if (j==lent)  return i - j;
	else return -1;
}

next数组求解

4.树

1.树的逻辑结构

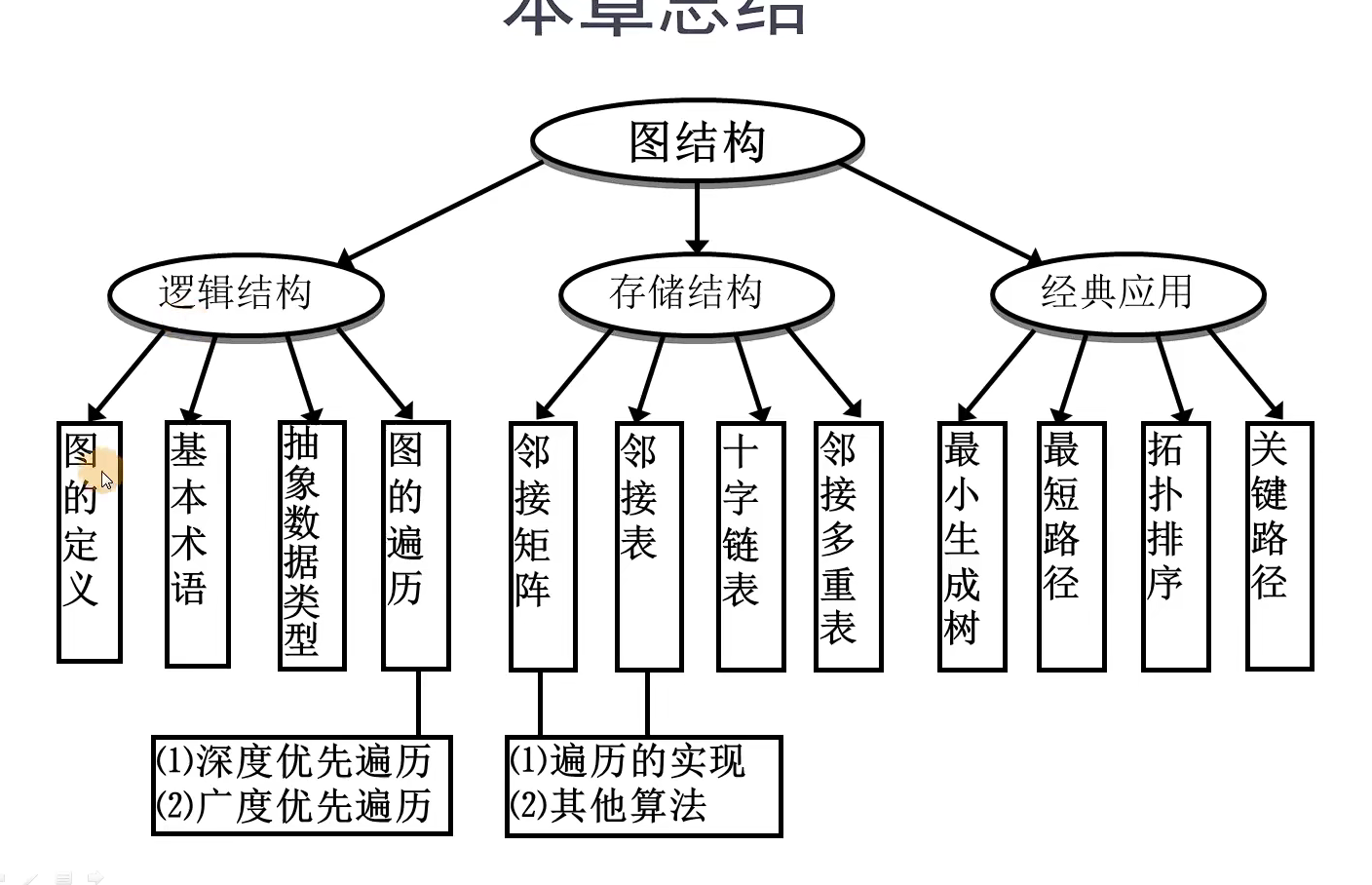
树的定义

结点的度:结点所拥有的子树的个数

树的度:树中各结点度的最大值

叶子结点

遍历:前序,后序,层序

2.树的存储结构

1.双亲表示法(静态链表,数组模拟链表)

层序遍历顺序存储

image-20211108124340151

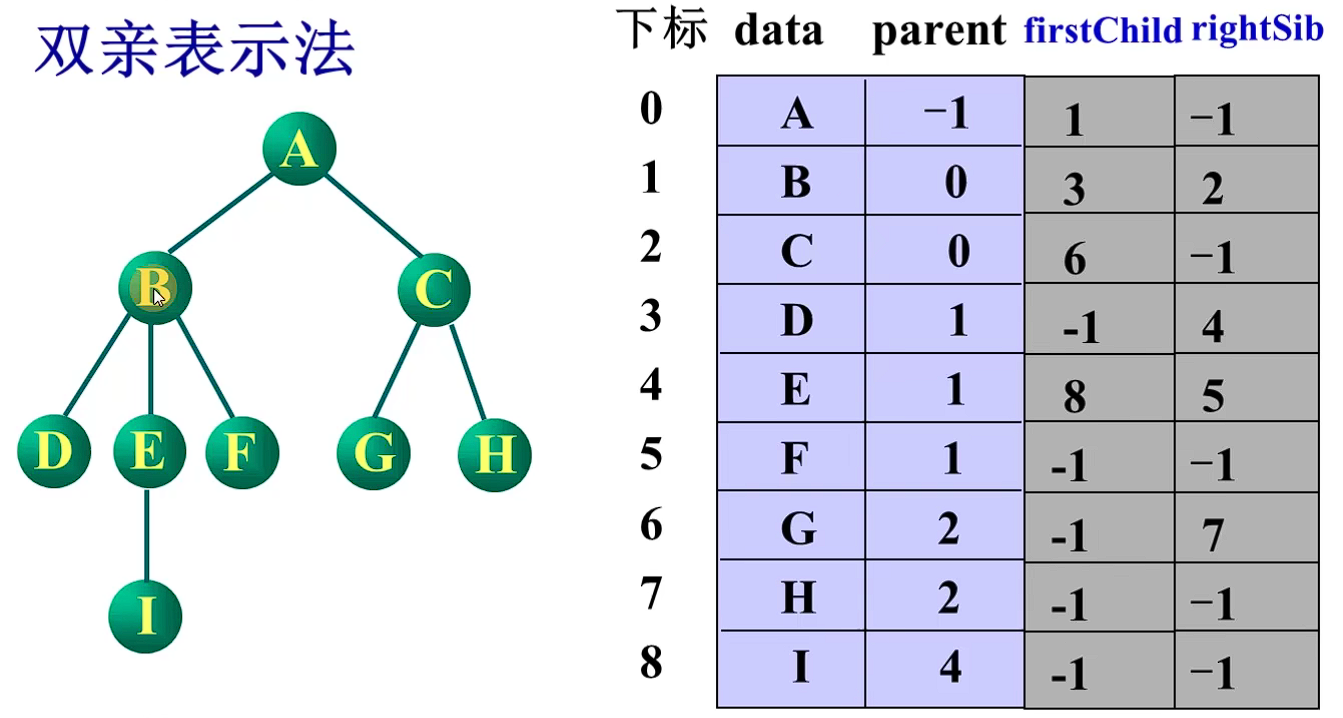
查找双亲结点O(1)

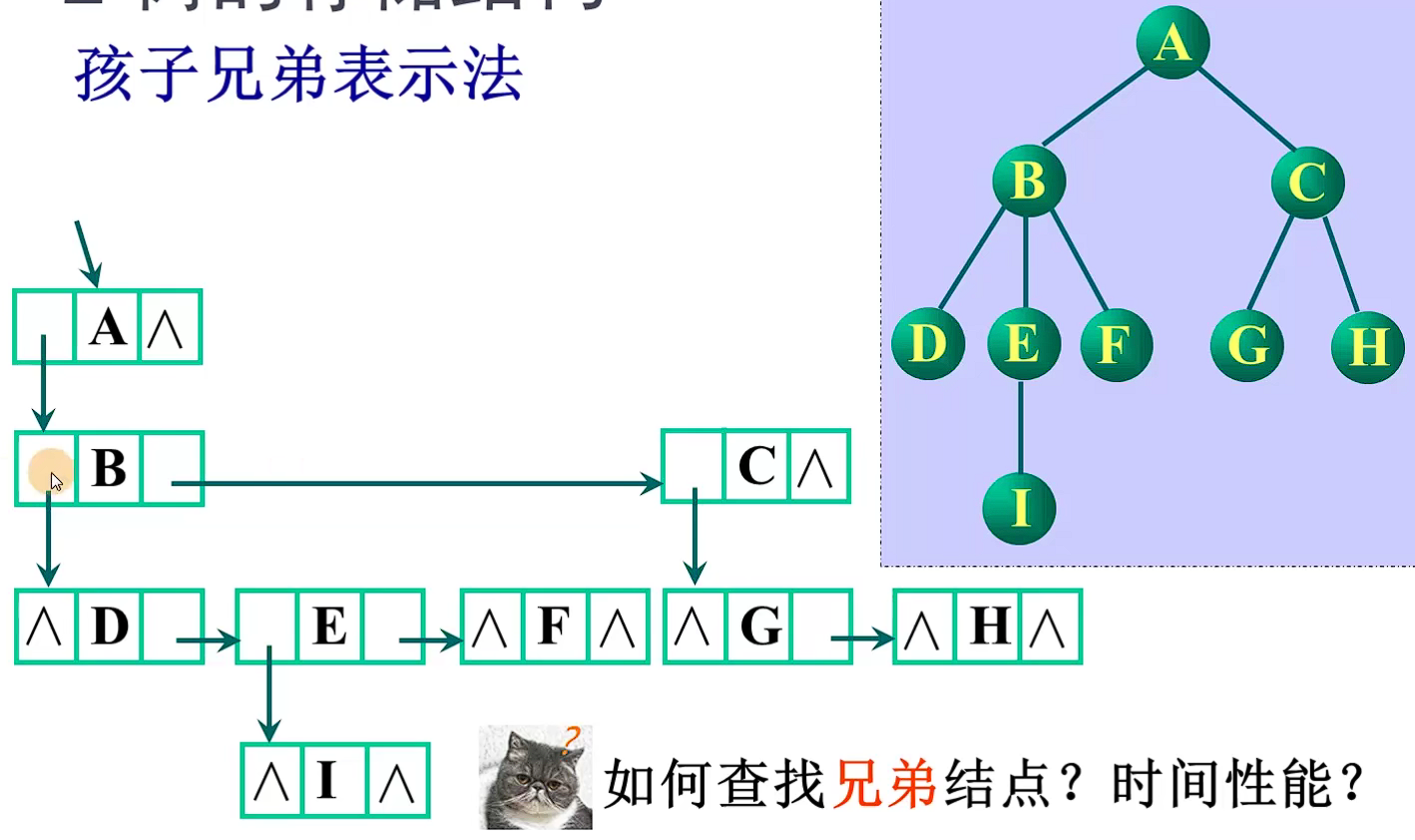
查找孩子结点O(n)(改进:增加firstChild字段

,增加rightSib 查找兄弟结点)

image-20211108125203153

-1的特殊作用:模拟空指针

2.孩子链表表示法

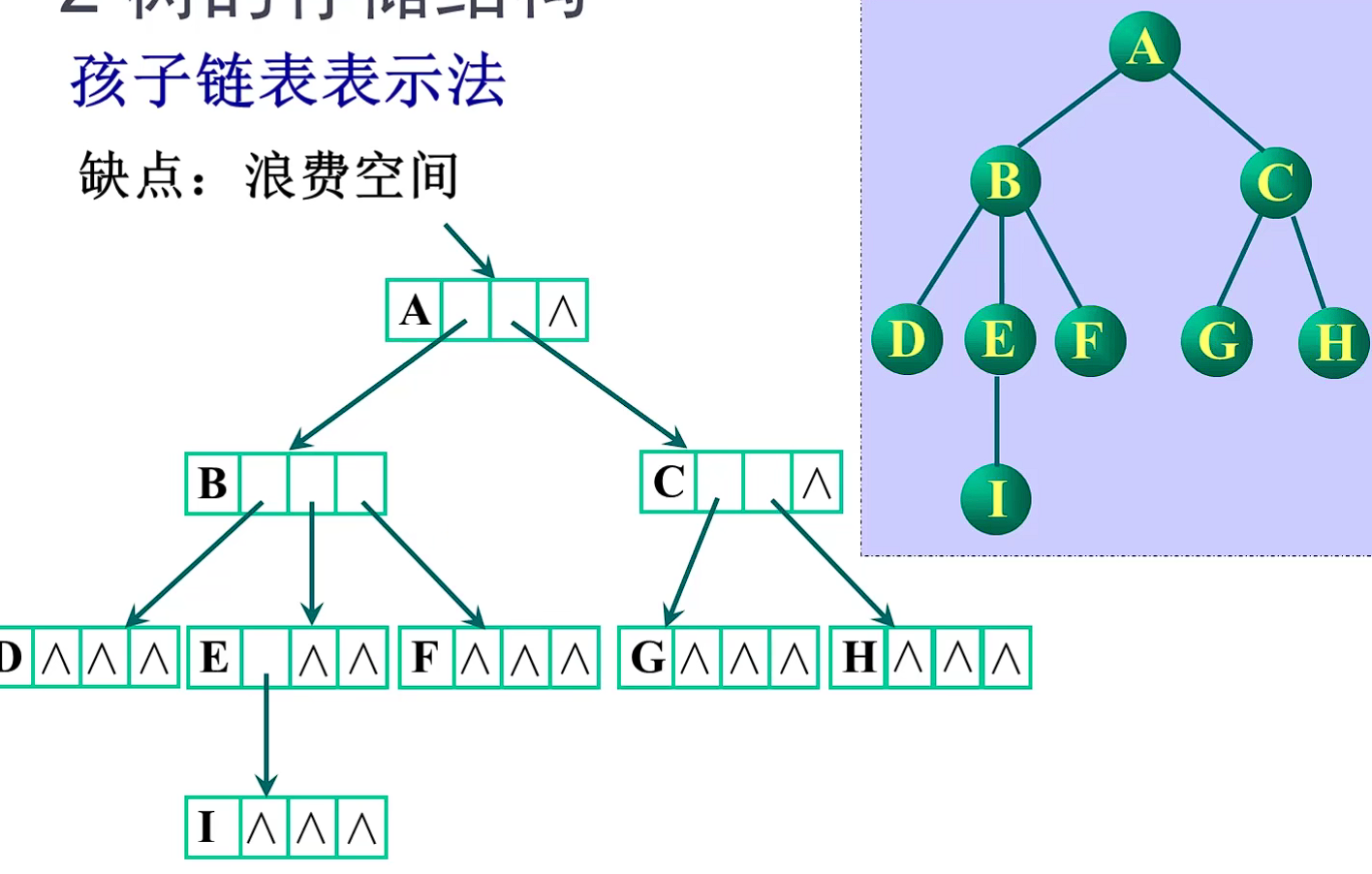
方案1 指针域的个数等于树的度

image-20211108125509426

缺点:浪费空间

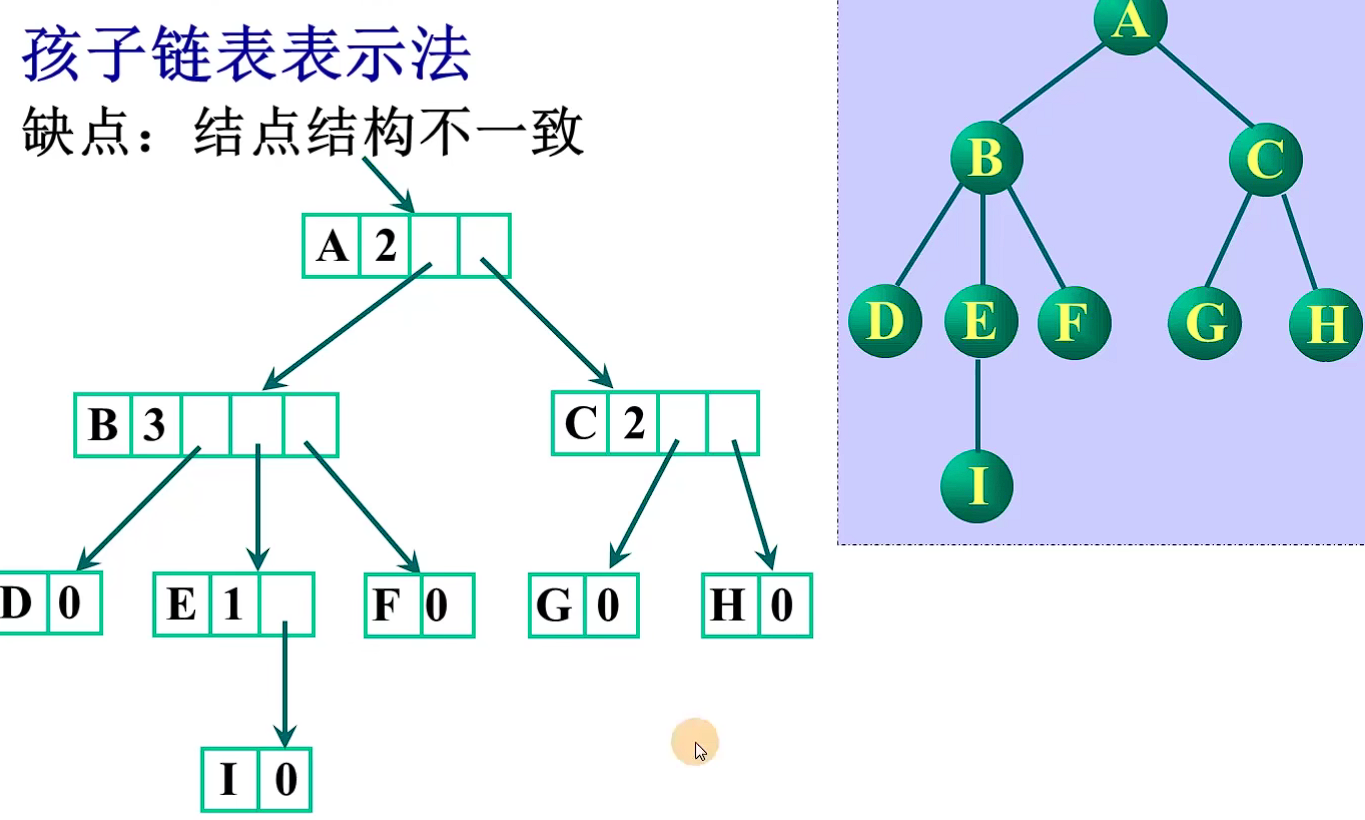
方案2 指针域的个数等于该结点的度

缺点:结点结构不一致

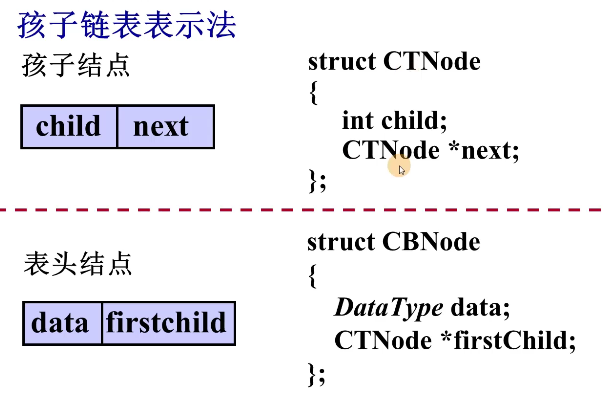
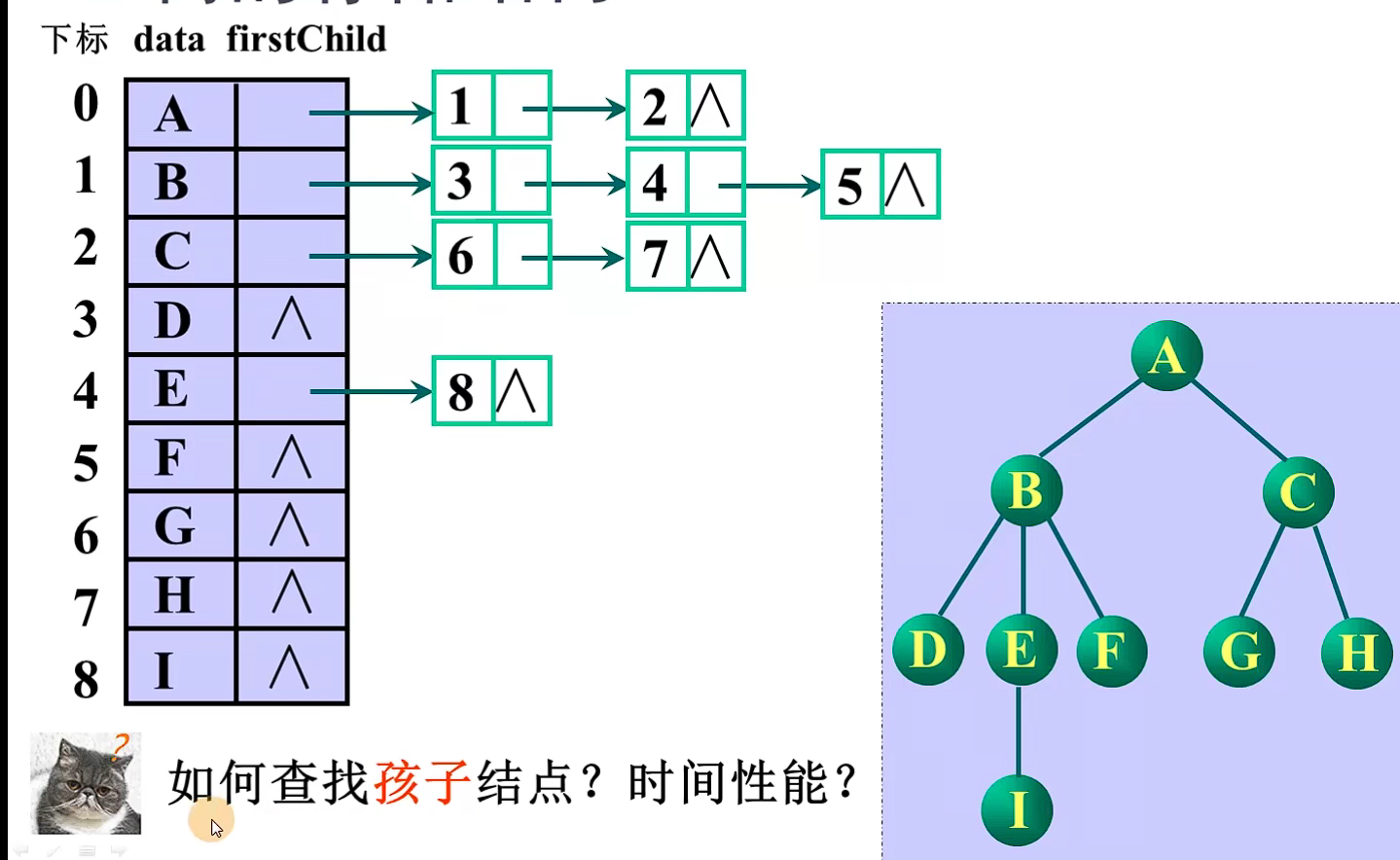
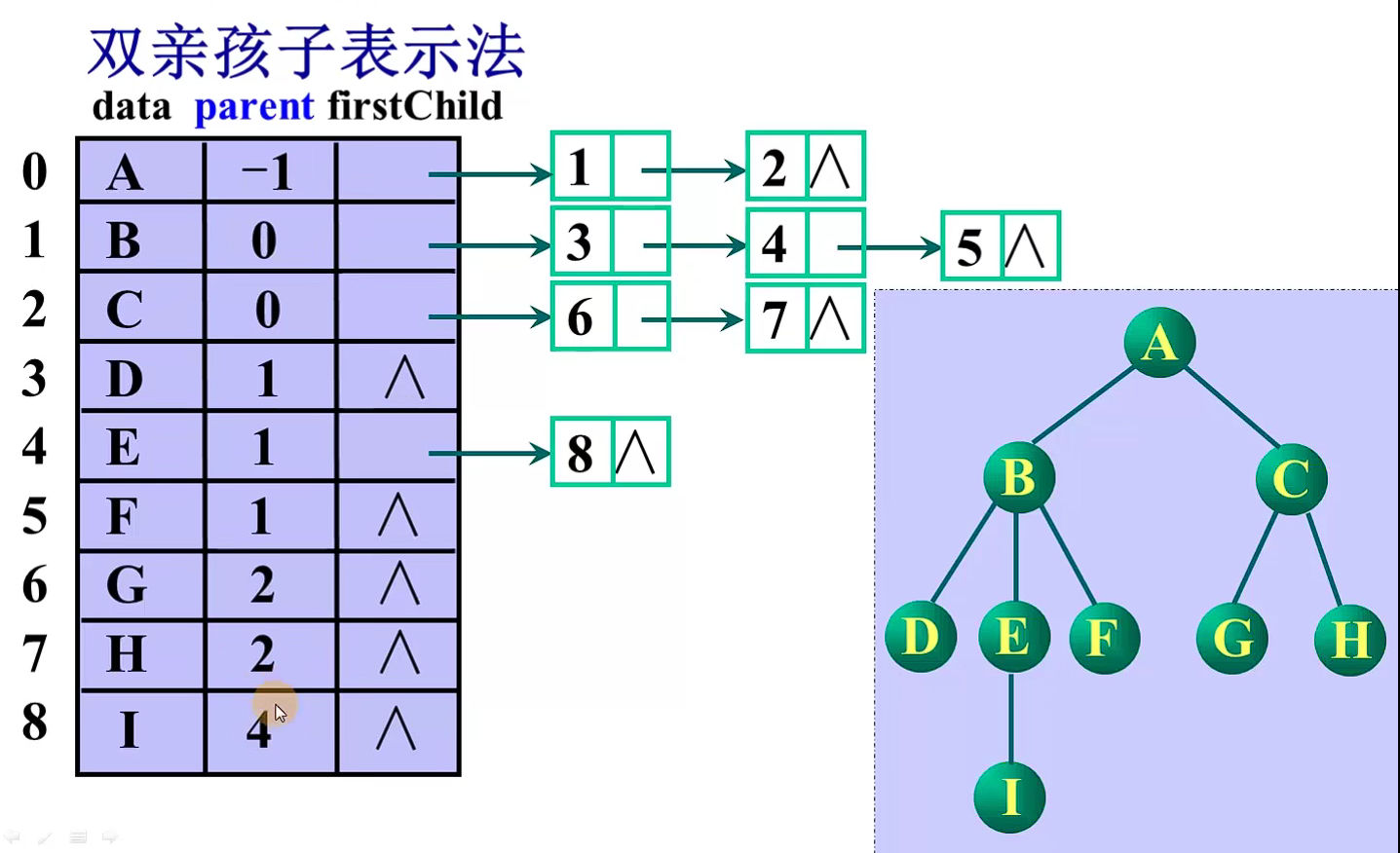
方案3 孩子链表表示法

image-20211108125911580

image-20211108130000754

image-20211108130214599

查找孩子结点 O(1)

查找双亲结点 逐个遍历结构体数组的链表O(n)

3改进:双亲孩子表示法

image-20211108130322177

4.孩子兄弟表示法

image-20211108130700686

image-20211108130809760

3.二叉树的逻辑结构

1.二叉树的逻辑结构

1.二叉树的定义

二叉树是n个结点的有限集合,该集合或者为空集(称为空二叉树)

,或有一个根节点和两棵互不相交的,分别称为根节点的左子树和右子树的二叉树组成.

2.特点

(1)没有结点最多有两棵子树

(2)二叉树是有序的

3.二叉树基本形态(5种)

4.特殊二叉树

(1)斜树

左斜树,右斜树

特点:每一场只有一个结点,斜树的节点个数与其深度相同

(2)满二叉树 所有分支结点都存放于左子树和右子树,并且所有叶子节点都在同一层上. 特点:叶子只能出现在最下一层,只有度为0和度为2的结点

(3)完全二叉树

对一颗具有n个结点的二叉树按层序编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同

在满二叉树中,从==最后一个结点==开始,连续去点任意一个结点,既是一个完全二叉树

特点

1.叶子结点只能出现在最下两层且最下层叶子结点都集中在二叉树的左边

2.完全二叉树中如果有度为一的结点,只可能有一个,且该节点只有左孩子

3.深度为k的完全二叉树在k-1层上一定是满二叉树

4.在同样节点个数的二叉树中,完全二叉树的深度最小

2.二叉树的基本性质

1.二叉树的第i层上最多有2^(i-1)个结点

2.一个深度为空的二叉树中,最多有2^k-个节点,最少有k个结点

深度为k且具有2^k-1 个结点的二叉树一定是满二叉树,深度为k且具有k个结点的二叉树不一定是斜树

3.叶子结点为n0,度为2的结点数位n2,则n0=n2+1

完全二叉树的性质

性质4:具有n个结点的完全二叉树的深度为不大于$\log_2n$的整数+1

image-20211108140834048

4.二叉树的存储结构及其实现

1.二叉树的存储结构

1.顺序存储

按完全二叉树的形式对二叉树进行编号存取到对应位置的数组中

存储斜树或一般二叉树比较浪费空间

2.链式存储

image-20211108143112221

struct BiNode{
	DataType data;//数据域
	BiNode *lchild,*rchile;//指向左右孩子
}

具有n个结点的二叉链表中,有n+1个空指针(n个结点有2n个指针,n-1条边,每一条边对应一个指针,所以空指针个数为(2n-n+1=n+1)

image-20211108144138726

image-20211108144341861

2.二叉树的遍历

(1)前序遍历

①访问根节点;

②前序遍历根节点的左子树

③前序遍历根节点的右子树

void  BiTree::PreOrder(BiNode *bt)
{
	if(bt==NULL)//递归调用结束的条件
	return;
	else{
	vist(bt->data);//访问根节点的数据域
	PreOrder(bt->lchild);//前序递归遍历根节点的左子树
	PreOrder(bt->rchild);//前序遍历根节点的右子树
	}
}

(2)中序遍历

若二叉树为空,则空操作返回

否则:

①中序遍历根节点的左子树

②访问根结点

③中序遍历根节点的右子树

void  BiTree::InOrder(BiNode *bt)
{
	if(bt==NULL)//递归调用结束的条件
	return;
	else{
	InOrder(bt->lchild);//中序递归遍历根节点的左子树
	vist(bt->data);//访问根节点的数据域
	InOrder(bt->rchild);//中序遍历根节点的右子树
	}
}

(3)后序遍历

若二叉树为空,则空操作返回

否则:

①后序遍历根节点的左子树

②后序遍历根节点的右子树

③访问根结点

void  BiTree::PreOrder(BiNode *bt)
{
	if(bt==NULL)//递归调用结束的条件
	return;
	else{
	PreOrder(bt->lchild);//后序递归遍历根节点的左子树
	PreOrder(bt->rchild);//后序遍历根节点的右子树
	vist(bt->data);//访问根节点的数据域
	}
}

二叉树的层序遍历

从上至下,从左到右的顺序对结点逐个访问

①队列Q初始化

②如果二叉树非空,将根指针入队

③循环直到队列为空

1.q=队列Q的对头元素出队

2.访问q的数据域

3.若结点q存在左孩子,则将左孩子指针入队

4.若结点q存在右孩子,则将有孩子指针入队

void Bitree::LeverOrder()
{
	if(root==NULL)
	return ;//二叉树为空,算法结束
	else{
		quenue.enQueue(root);//根指针入队
		while(!queue.isEmpty()){
			q=queue.deQueue();//对头出队
			visit(q->data);//输出对头元素数据
			if(q->lchild!=NULL) //左孩子指针入队
				queue.enQueue(q->lchile);
			if(q->rchild)//有孩子指针入队
				queue.enQueue(q->rchild);
		}
	}
}

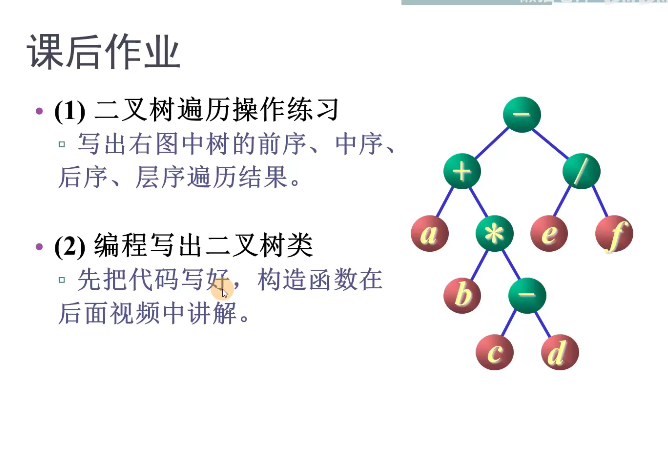
image-20211109172458681

前序 -+a*b-cd/ef
中序 a+b*c-d-e/f
后序 abcd-*+ef/-
层序 -+/a*efb-cd

5.树,森林与二叉树的转换

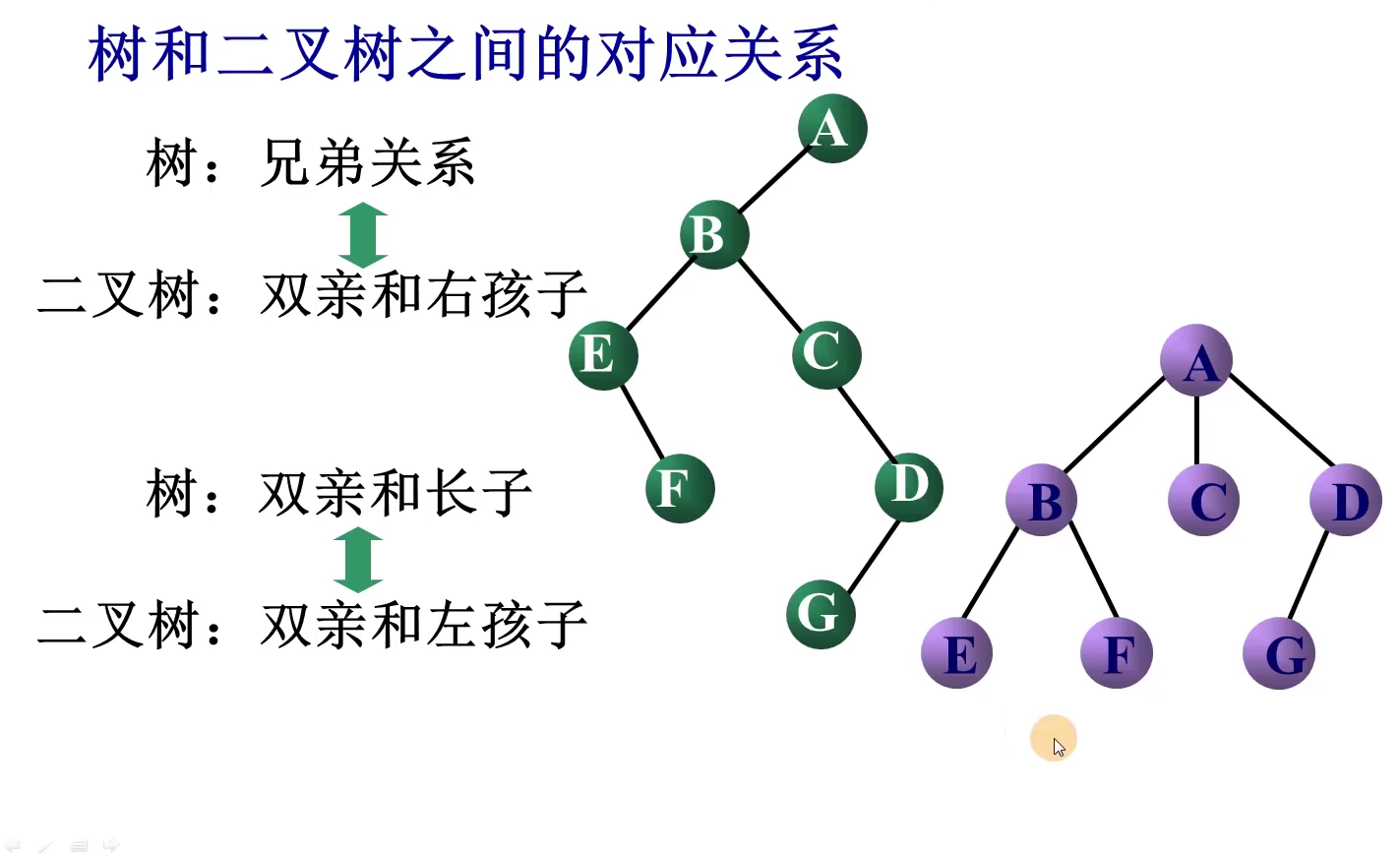
image-20211118173927925

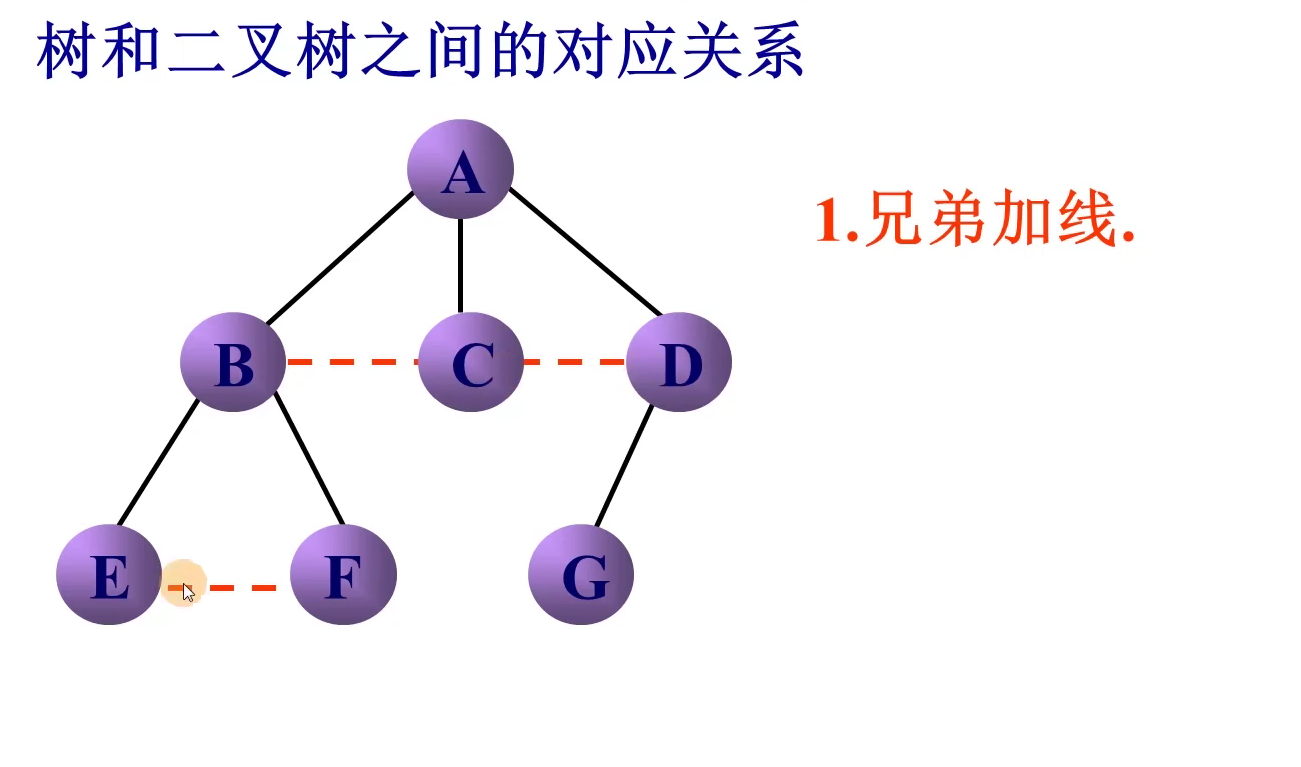
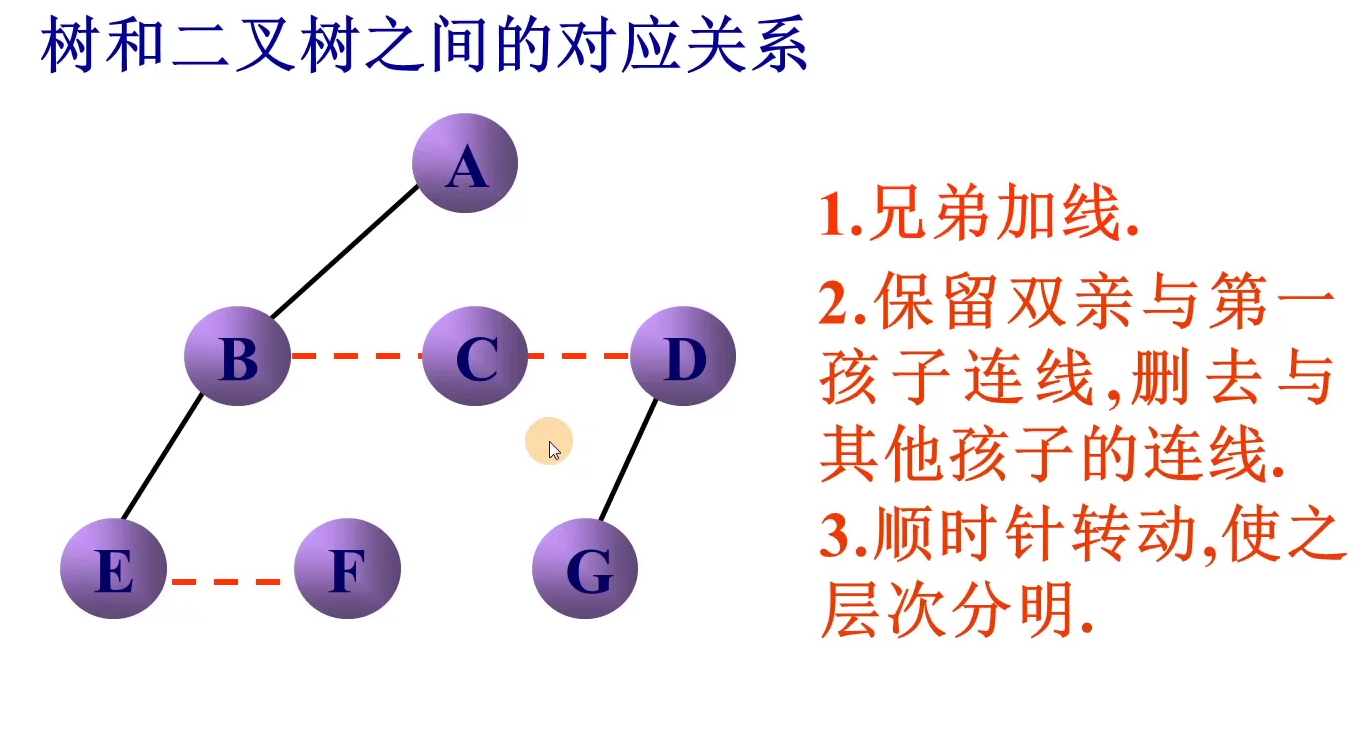
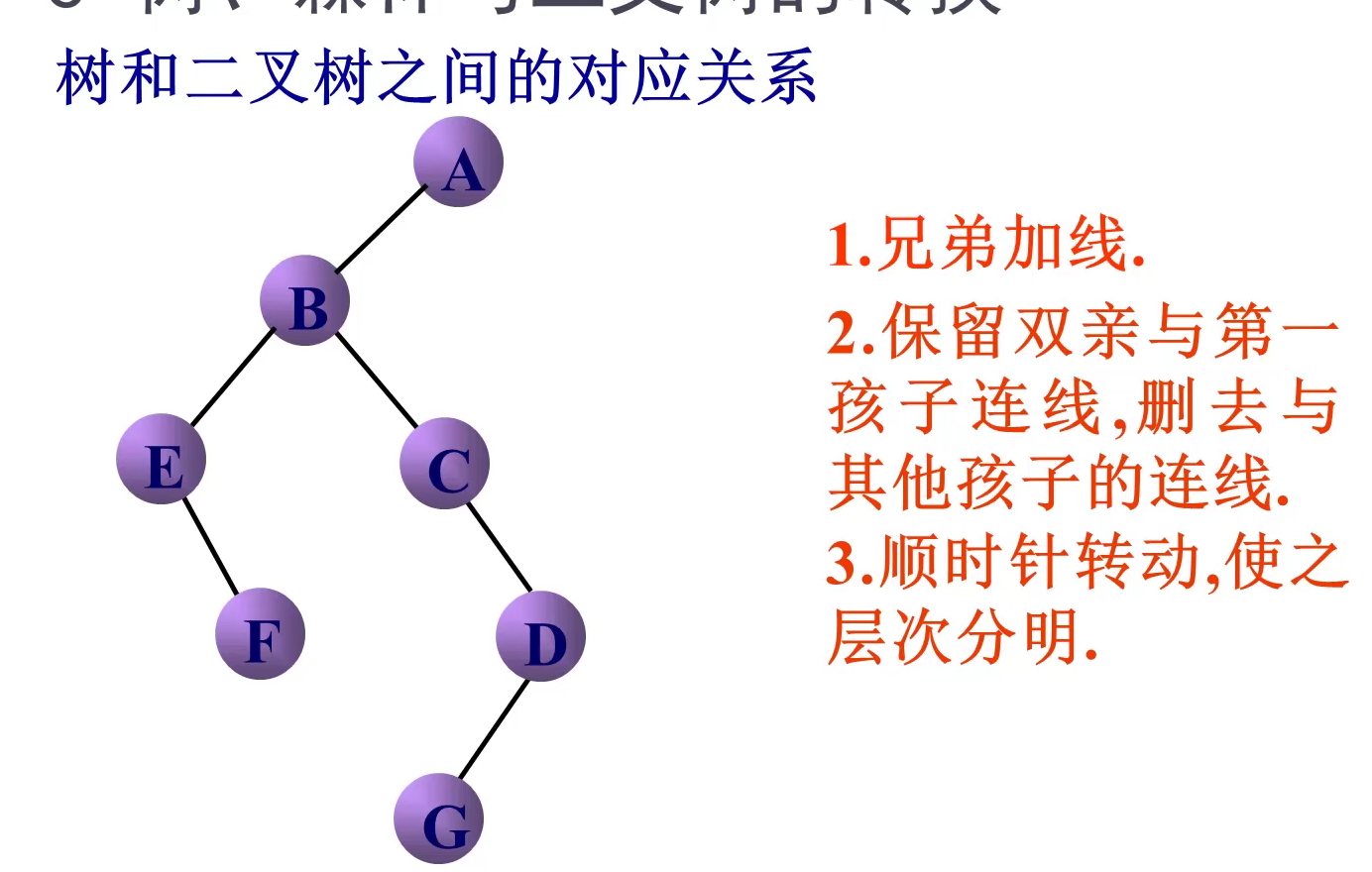
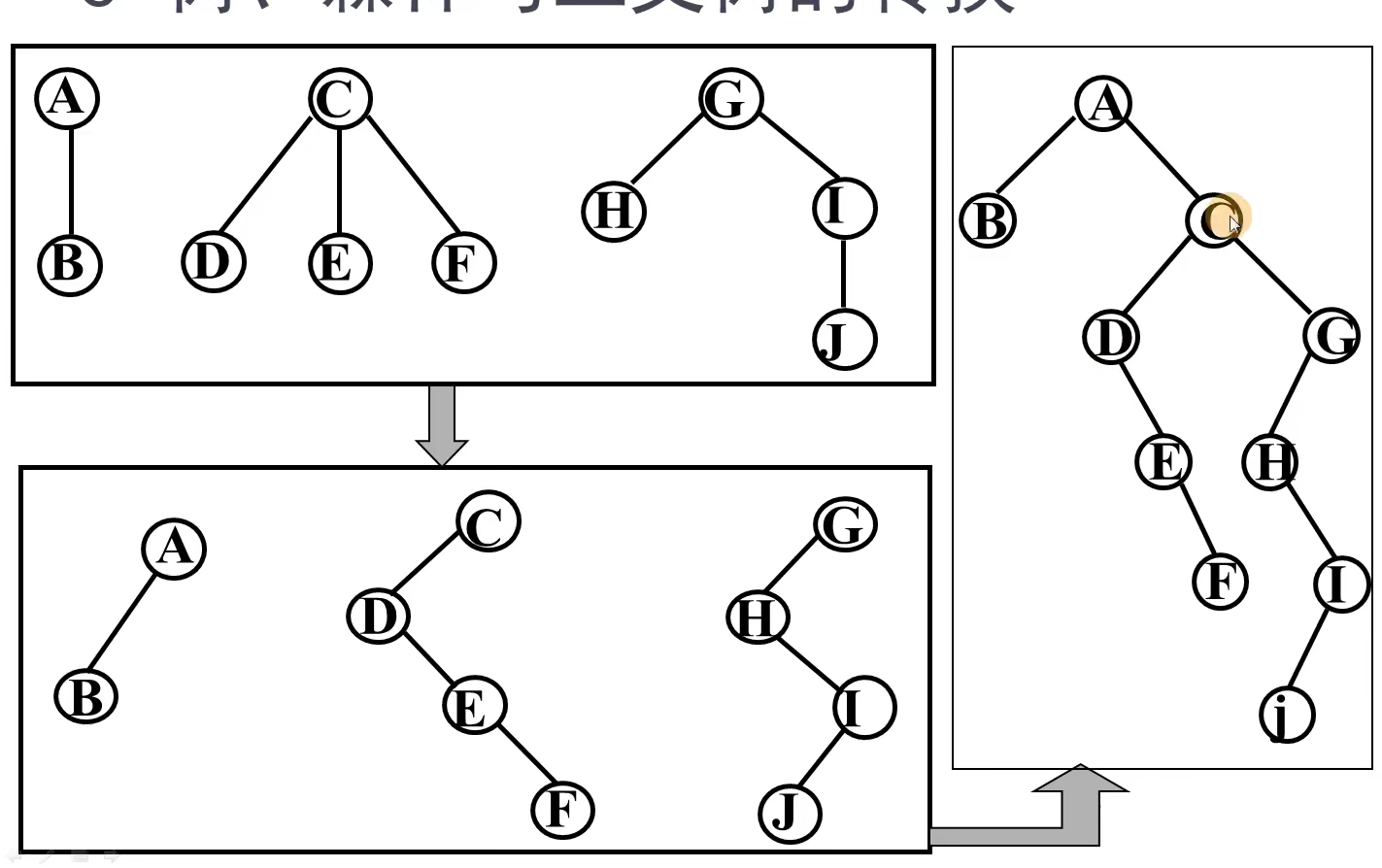
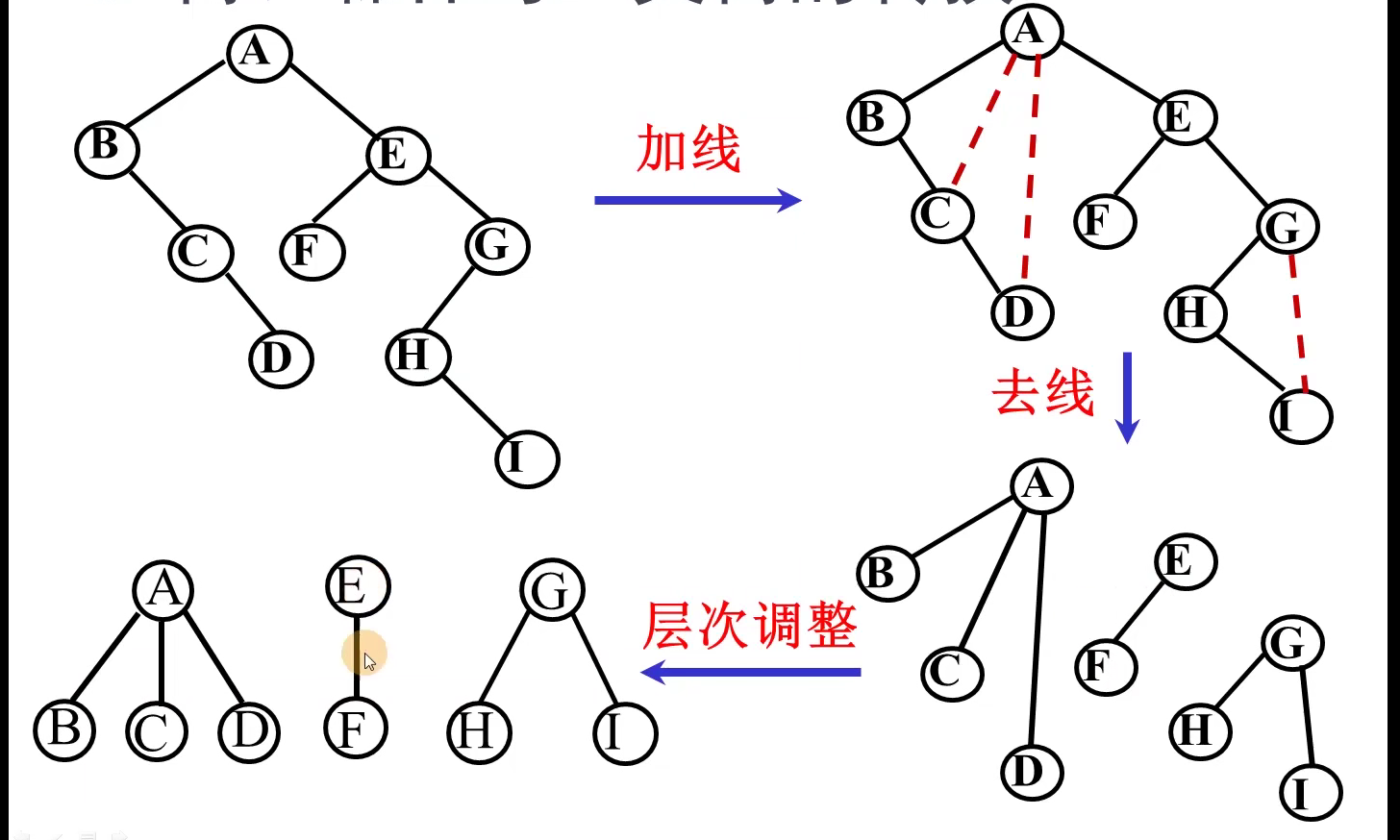
转换方法

image-20211118174149815

image-20211118174543250

image-20211118174250816

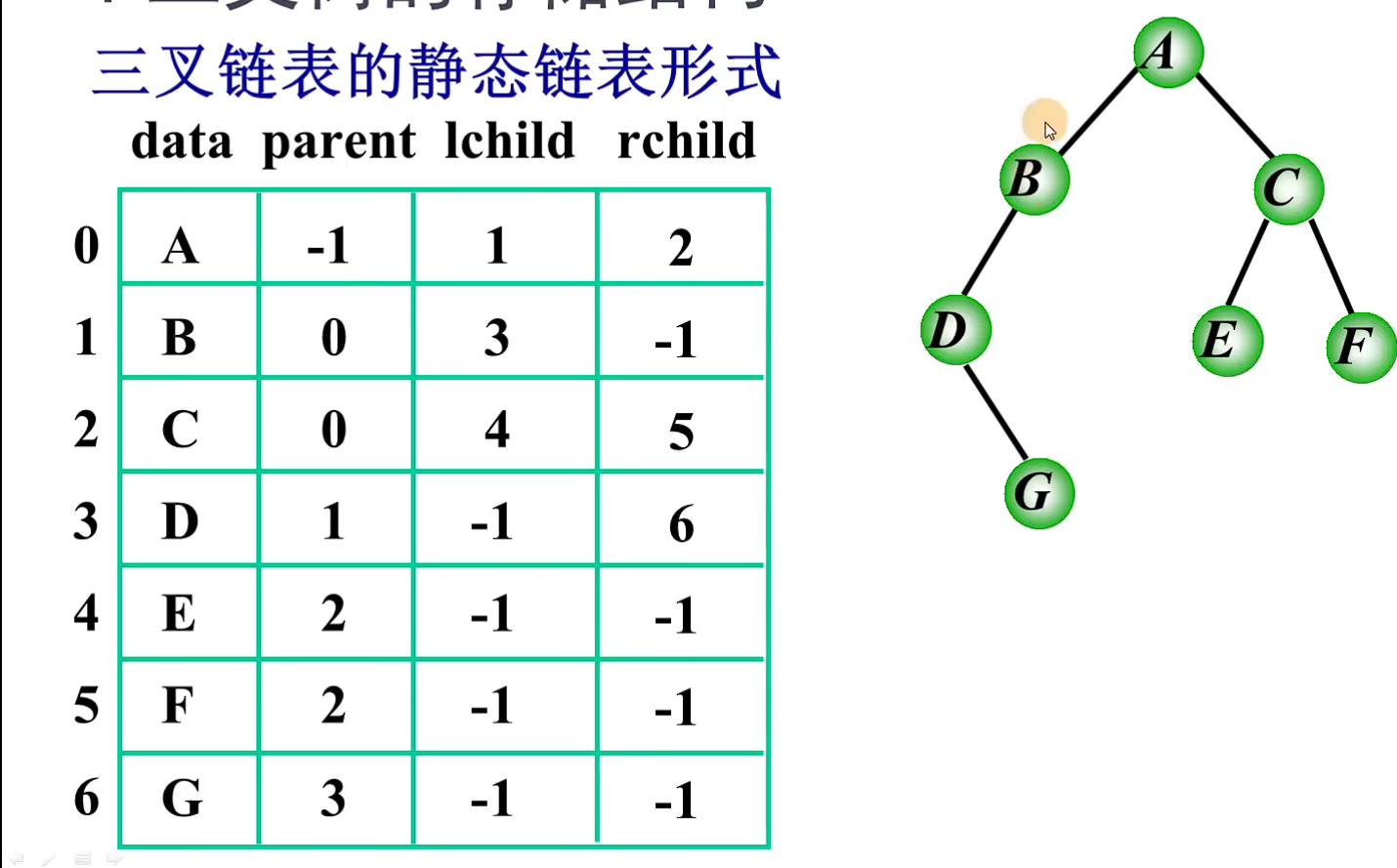
数转换为二叉树后的遍历顺序不变

image-20211118175043643

image-20211118175022264

image-20211118175159896

image-202111181754190146.二叉树的遍历的非递归算法

7.哈夫曼树与哈夫曼编码

中序遍历指适用与二叉树

5.图

1.图的基础

image-20211123222226306

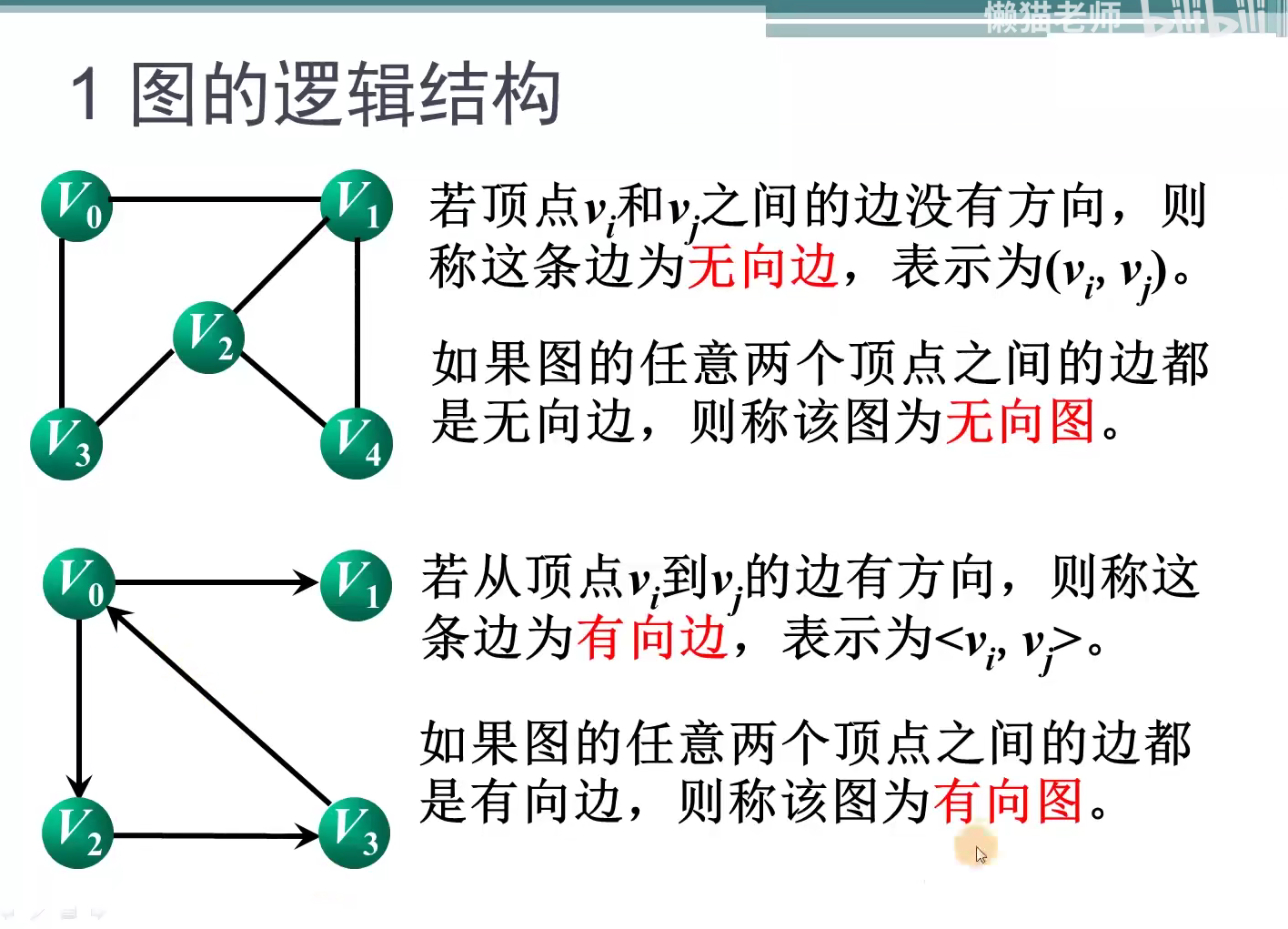
image-20211123222407765

image-20211123222527083

image-20211123222656113

image-20211123222749059

不同结构中逻辑关系

线性结构 树结构 图结构
线性关系 层次关系 任何两个顶点之间都可能有关系
元素之间前驱和后继 双亲和孩子 邻接

image-20211123223325296

image-20211123223457761

image-20211123223551214

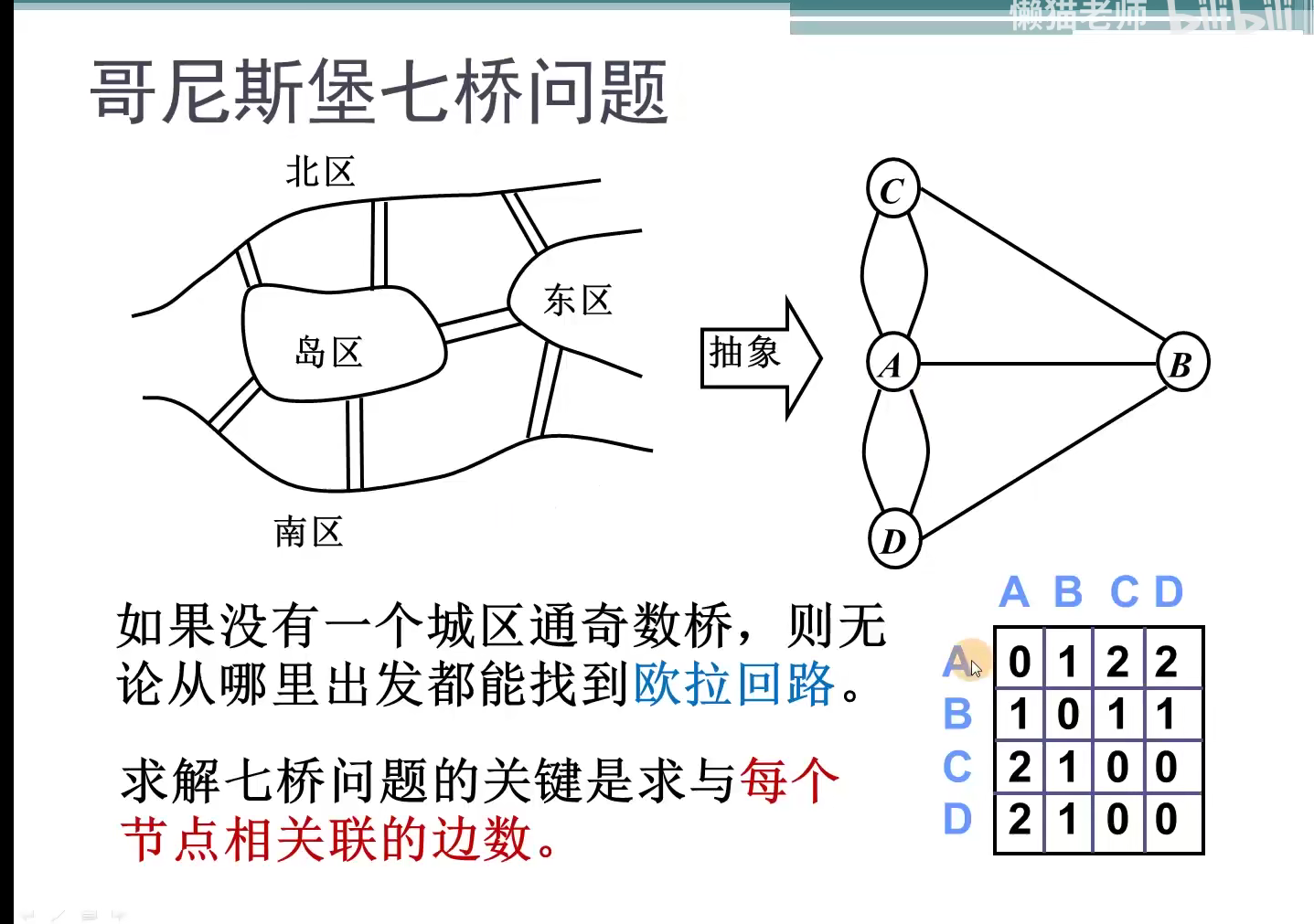
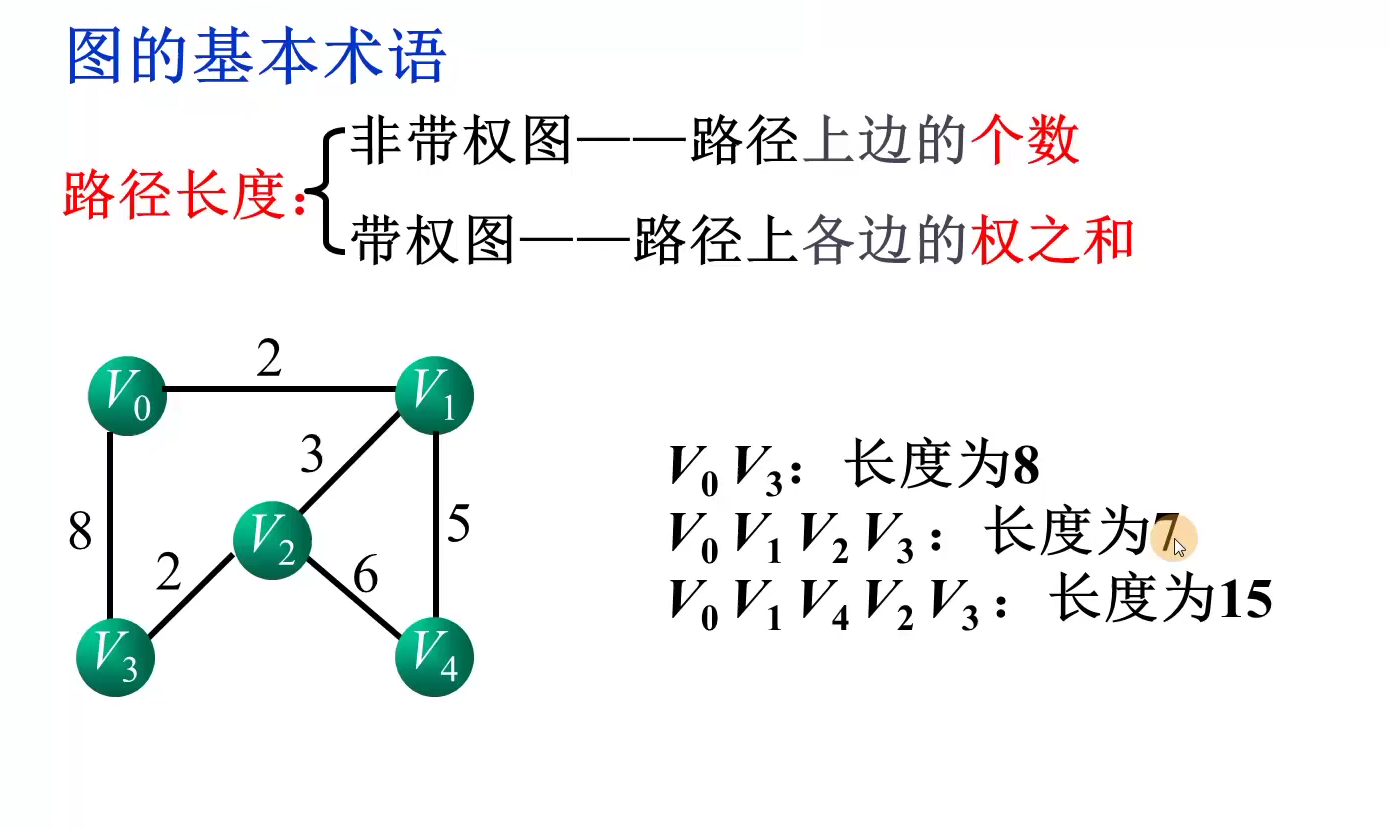
n个顶点，e条边的无向图，各顶点的度数之和与边数之和的关系

$$ \sum_{i=1}^{n}TD(v_i)=2e $$

n个顶点，e条边的有向图，各顶点的入度数之和与各顶点的出度之和与边数之和的关系

$$ \sum_{i=1}^{n}ID(v_i)=\sum_{i=1}^{n}OD(v_i)=e $$

image-20211123224120691

image-20211123224332013

image-20211123224437692

image-20211123224511734

image-20211123224550676

image-20211123224642529

image-20211123224731675

image-20211123224908263

2.邻接矩阵

image-20211124091954309

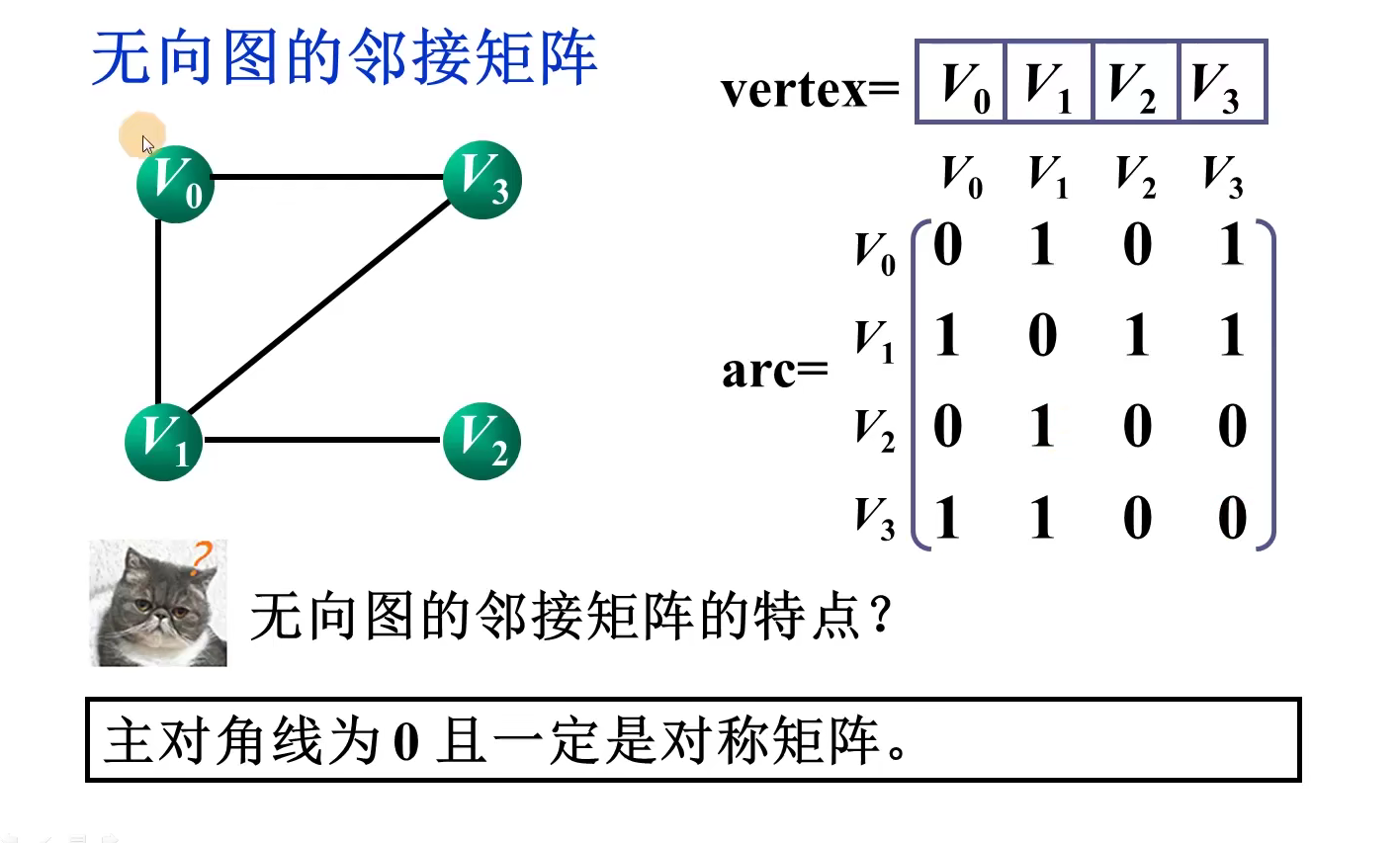
image-20211124092237125

顶点i的度：邻接矩阵的第i行或第i列非零元素个数

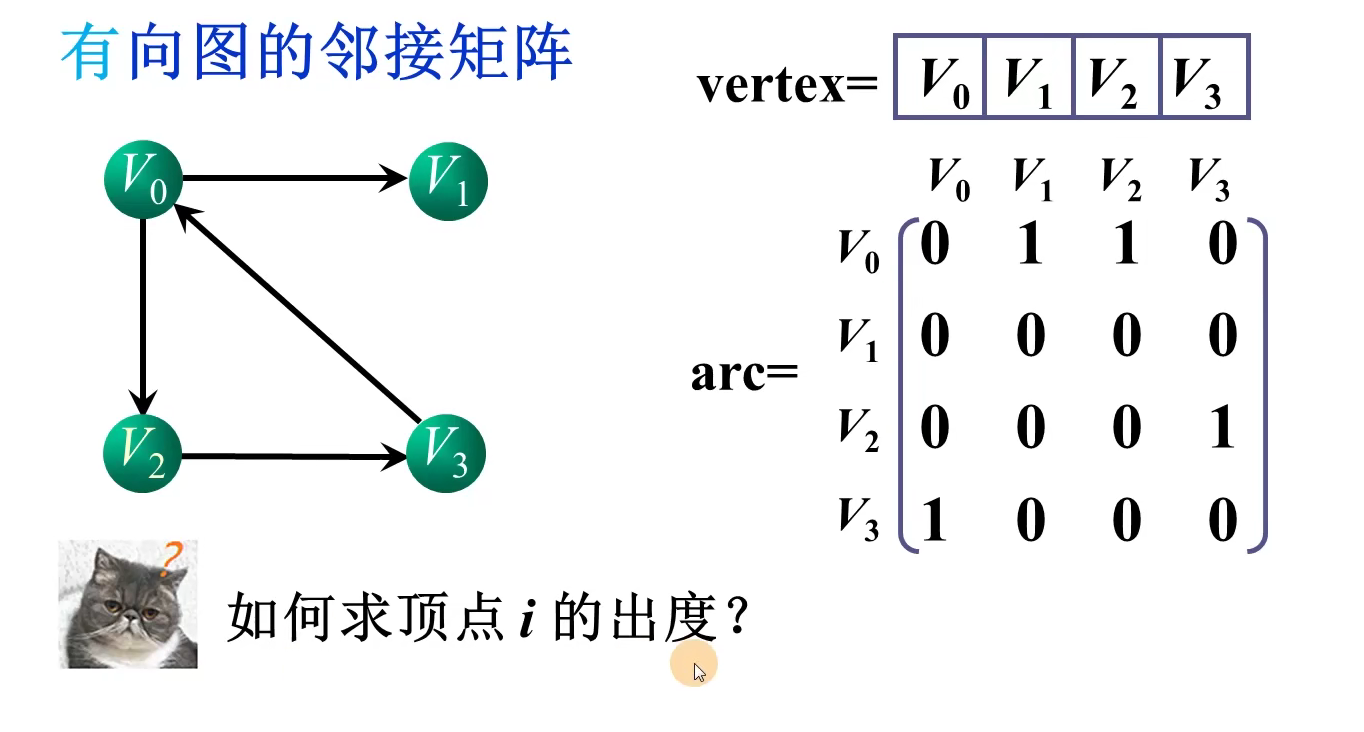
i，j之间是否存在边：测试邻接矩阵相应位置的元素arc[i][j]是否为1

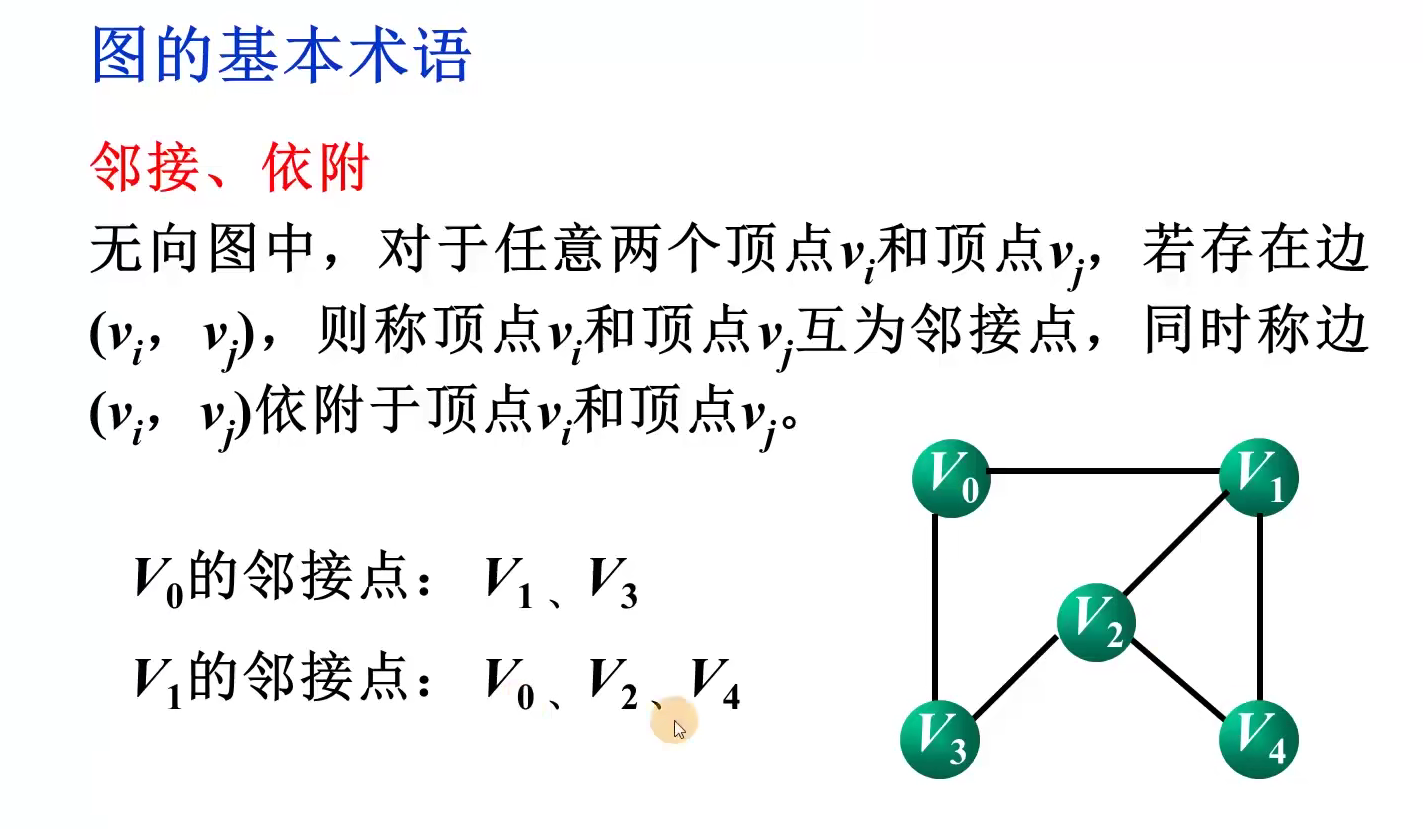
顶点i的所有连接点：将第i行扫描一遍，若arc[i][j]为1，则顶点j为顶点i的邻接点

image-20211124092953501

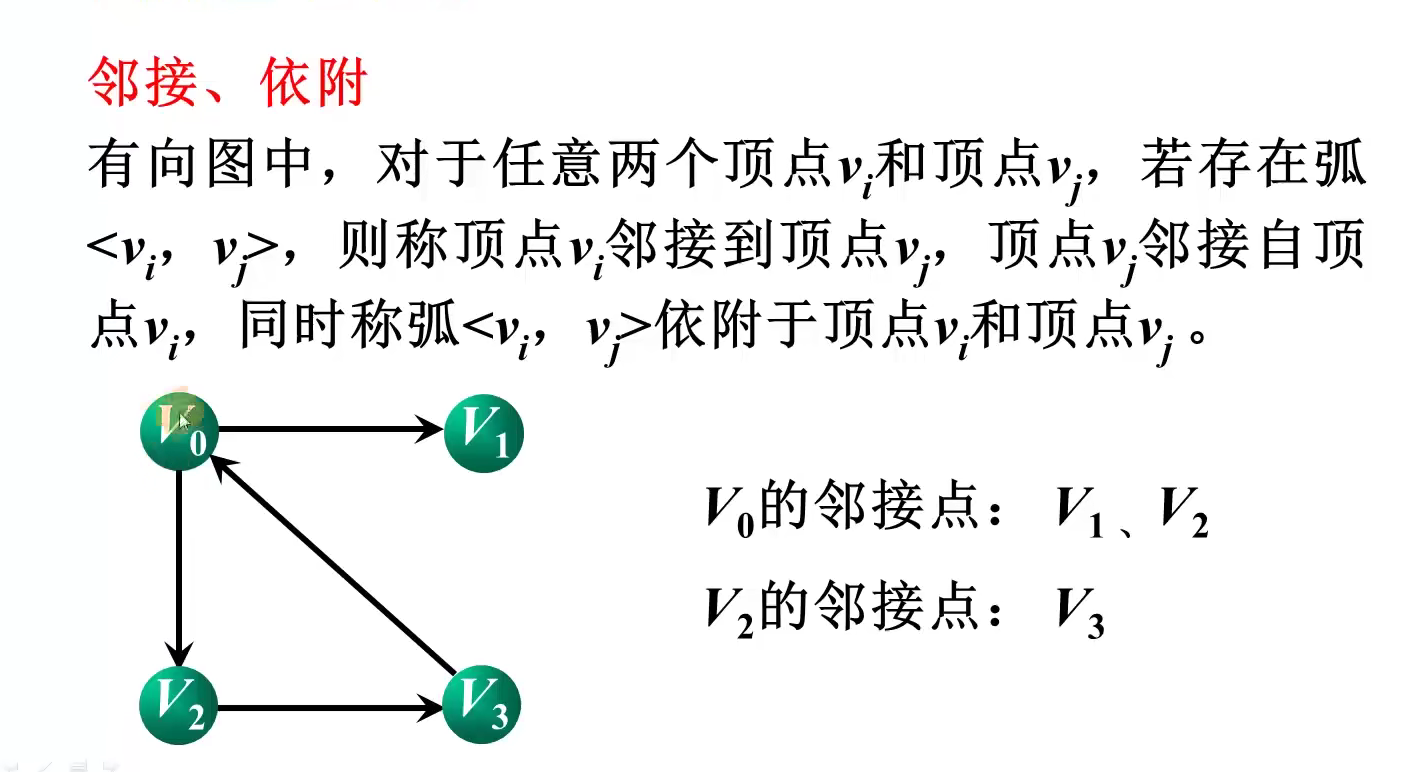
顶点i的出度：邻接矩阵的第i行非零元素个数

顶点i的入度：邻接矩阵第i列非零元素之和

i，j之间是否存在边：测试邻接矩阵相应位置的元素arc[i][j}是否为1

image-20211124093320839

image-20211124094420719

邻接矩阵类：

#include<iostream>
using namespace std;

void cinij(int& vi, int& vj)
{
	cout << "请输入该边依附的顶点编号" << endl;
	cin >> vi >> vj;
}


//无向图的邻接矩阵
#define DataType int
const int MAX_VERTEX = 10;//图的最大顶点数
class MGraph
{
public:
	MGraph(DataType v[],int n,int e);
	~MGraph();
	void DFSTraverse(int v);//深度优先遍历
	void BFSTraverse(int v);//广度优先遍历
	void display();//打印邻接矩阵和顶点数组
private:
	DataType vertex[MAX_VERTEX];//顶点数组
	int arc[MAX_VERTEX][MAX_VERTEX];//边
	int vettexNum, arcNum;//实际定点数和边数
};

//析构函数
MGraph::MGraph(DataType v[],int n,int e)
{
	vettexNum = n;
	arcNum = e;
	for (int i = 0; i < vettexNum; i++)
	{
		vertex[i] = v[i];//顶点数组初始化
	}
	for (int i = 0; i < vettexNum; i++)
	{
		for (int j = 0; j <vettexNum; j++)
		{
			arc[i][j] = 0;//初始化邻接矩阵
		}
	}
	for (int i = 0; i < arcNum; i++)
	{
		//依次输入每一条边
		int vi, vj;
		cinij(vi, vj);//输入边依附的顶点编号
		arc[vi][vj] = 1;//置有边标志
		arc[vj][vi] = 1;
	}

}

MGraph::~MGraph()
{
}

void MGraph::display()
{
	cout << "顶点数组为：" << endl;
	for (int i = 0; i < vettexNum; i++)
	{
		cout << vertex[i] << " ";
	}
	cout << endl;//打印顶点数组
	cout << "arc=" << endl;
	cout << " ";
	for (int i = 0; i < vettexNum; i++)
	{
		cout << " " << i;
	}
	cout << endl;//打印邻接矩阵
	for (int i = 0; i <vettexNum; i++)
	{
		cout << i << " ";
		for (int j = 0; j < vettexNum; j++)
		{
			cout << arc[i][j] << " ";
		}
		cout << endl;
	}

}

int main()
{
	int a[] = { 0,1,2,3 };
	MGraph m(a, 4, 4);
	m.display();

}

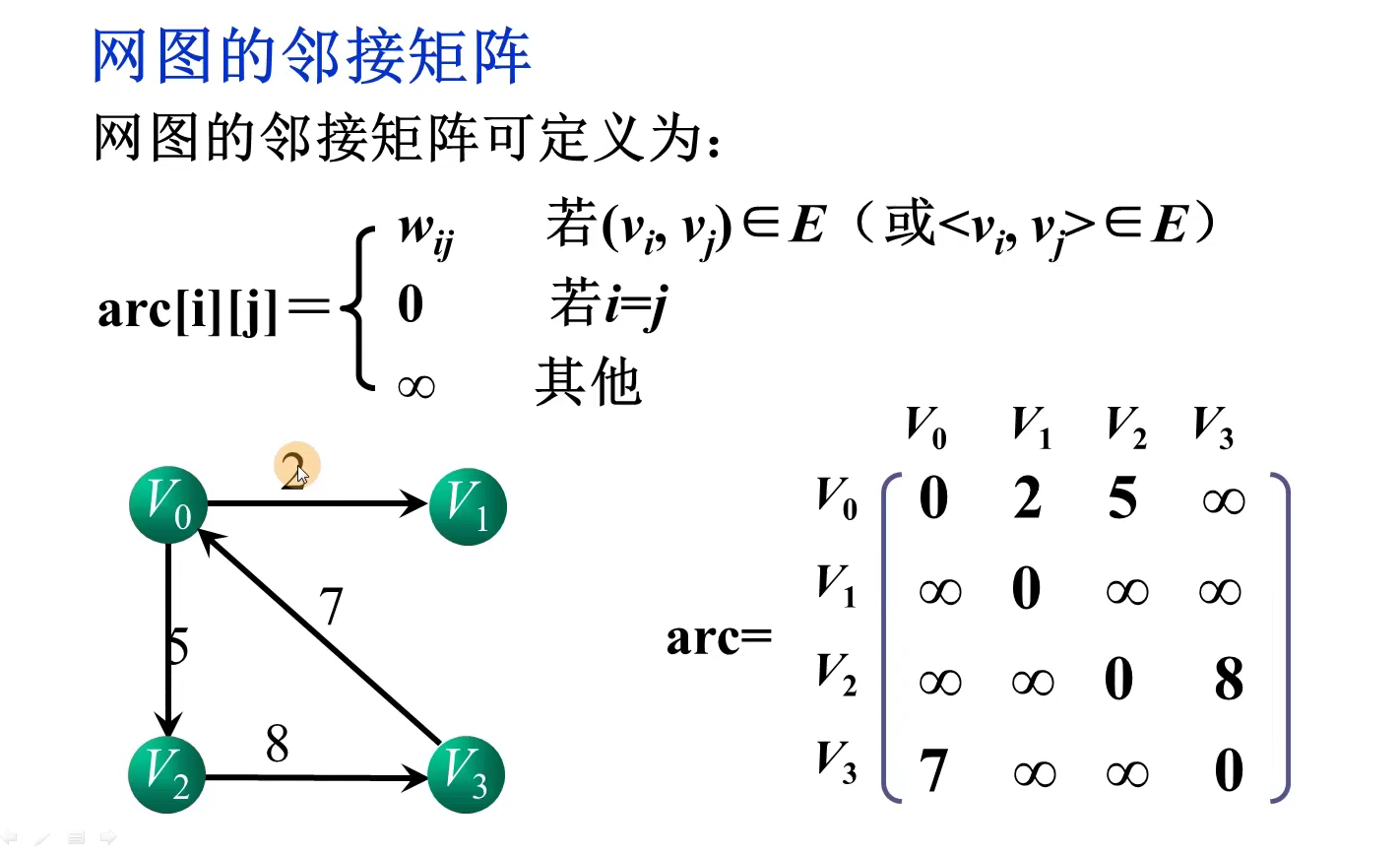
如果为稀疏图，会造成邻接矩阵的存储空间大量浪费

一个n个顶点e条边的图，其存储空间为O$(n^2)$

3.邻接表

image-20211124130231537

image-20211124130628239

n个顶点，边表所需空间为2e

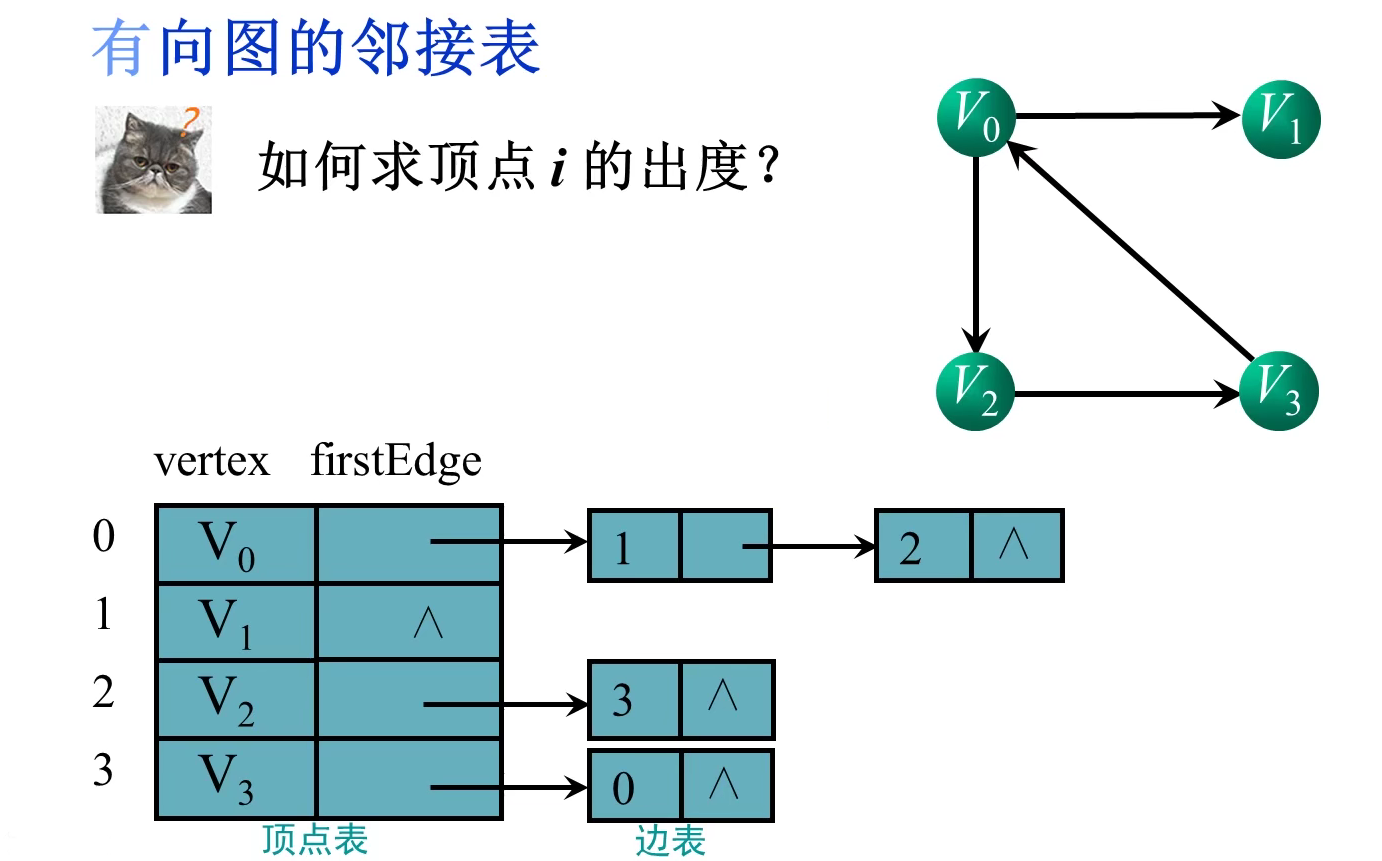
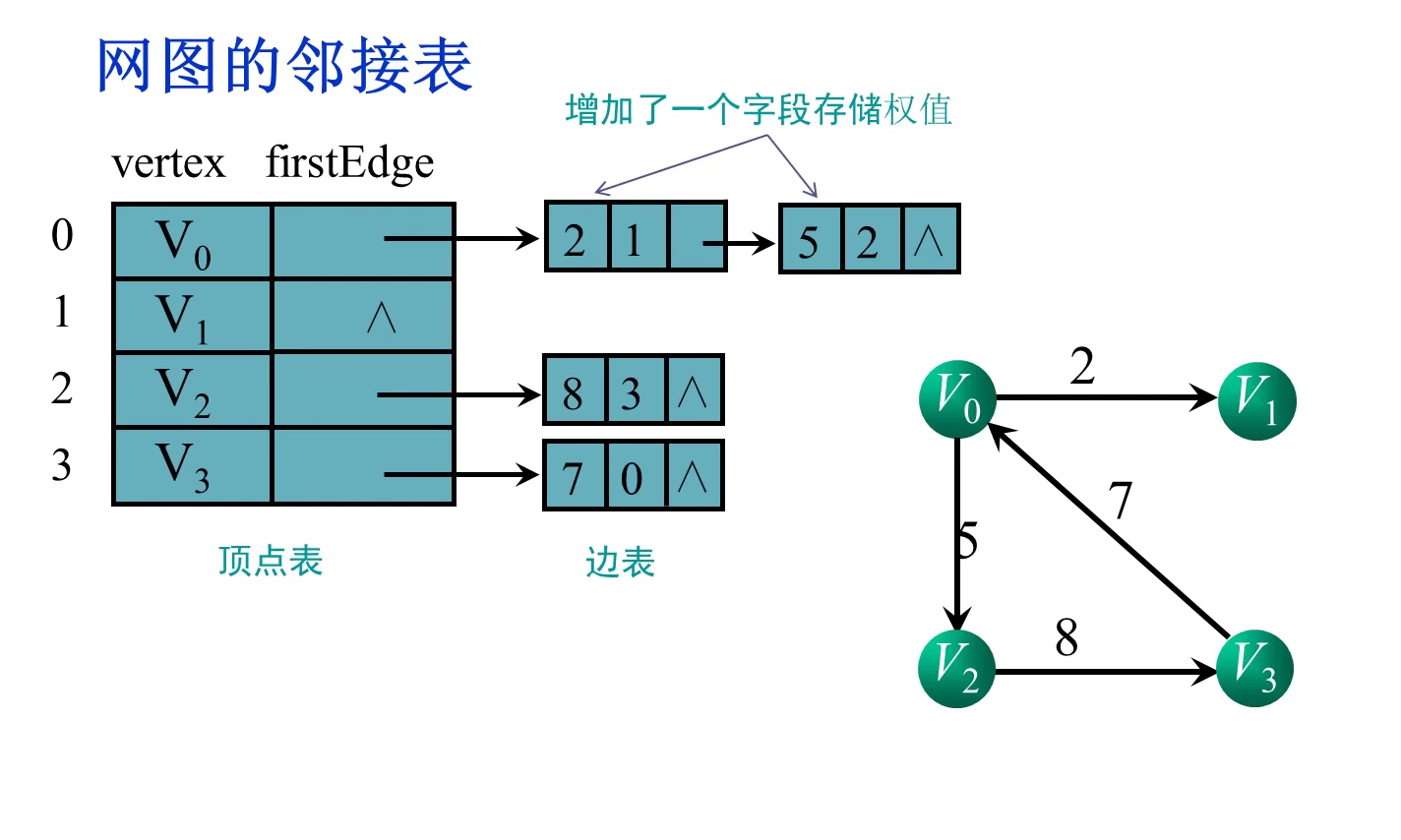
如何求顶点i的度：边表结点个数

判断顶点i和顶点j之间是否存在边：测试顶点i的便表中是否存在终点为j的结点

image-20211124132046224

顶点i的出度：顶点i的出边表中结点的个数

顶点i的入度：各顶点的出边表中以顶点i为终点的节点个数

顶点i的所有邻接点：遍历顶点i的边表，该边表中的所有顶点都是顶点i的邻接点

image-20211124132630269

void MGraph::display()
{
	cout << "顶点数组为：" << endl;
	for (int i = 0; i < vettexNum; i++)
	{
		cout << vertex[i] << " ";
	}
	cout << endl;//打印顶点数组
	cout << "arc=" << endl;
	cout << " ";
	for (int i = 0; i < vettexNum; i++)
	{
		cout << " " << i;
	}
	cout << endl;//打印邻接矩阵
	for (int i = 0; i <vettexNum; i++)
	{
		cout << i << " ";
		for (int j = 0; j < vettexNum; j++)
		{
			cout << arc[i][j] << " ";
		}
		cout << endl;
	}

}
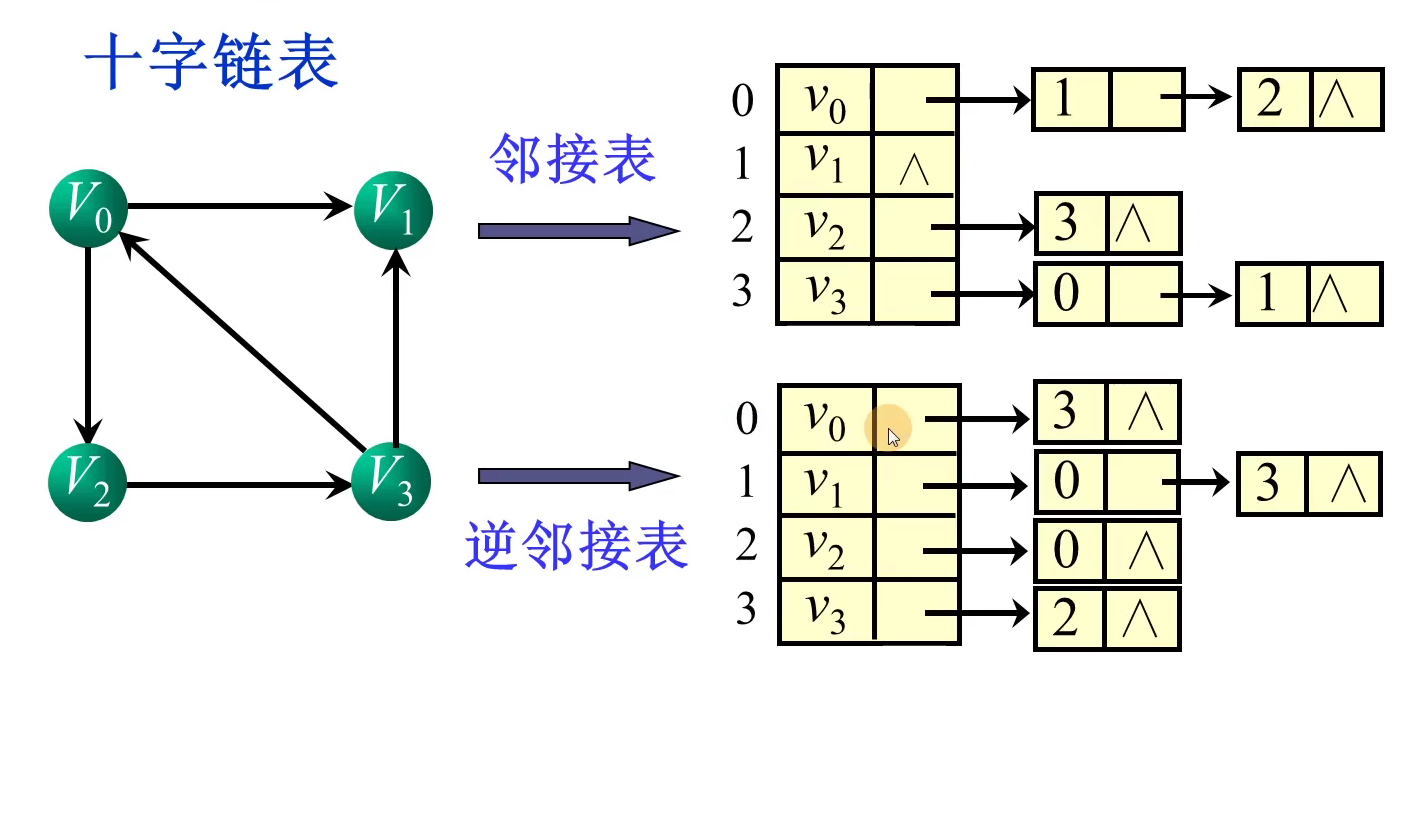
//邻接表存储有向图
//边表
typedef struct AdjVexNode
{
	int adivex;//邻接点域，变得终点在定点表中的下标
	struct AdjVexNode* next;//指针域，指向边表中的下一个结点
}ArcNode;
//定点表
typedef struct Vettexnode
{
	DataType vettex;//数据源，存放顶点信息
	ArcNode* firstEdge;//指针域，指向边表中的第一个节点
}VettexNode;
class ALGraph
{
public:
	ALGraph(DataType v[],int n,int e);
	~ALGraph();
	void display();

private:
	VettexNode adjList[MAX_VERTEX];//定点表结构体数组
	int vertexNum, arcNum;//顶点个数，边的个数
};

ALGraph::ALGraph(DataType v[],int n,int e)
{
	vertexNum = n;
	arcNum = e;
	for (int i = 0; i < vertexNum; i++)
	{//输入定点信息，初始化定点表
		adjList[i].vettex = v[i];
		adjList[i].firstEdge = NULL;
	}
	//输入边的信息存储在边表中
	for (int i = 0; i < arcNum; i++)
	{
		int vi, vj;
		cinij(vi, vj);
		ArcNode *s = new ArcNode;
		s->adivex = vj;
		s->next = adjList[vi].firstEdge;
		adjList[vi].firstEdge = s;
	}
}

ALGraph::~ALGraph()
{
	for (int i = 0; i < vertexNum ;i++)
	{
		ArcNode* p;
		while (adjList[i].firstEdge)
		{
			p = adjList[i].firstEdge;
			adjList[i].firstEdge = adjList[i].firstEdge->next;
			delete p;
		}
	}
}

void ALGraph::display()
{
	for (int i = 0; i < vertexNum; i++)
	{
		cout << adjList[i].vettex << "——";
		ArcNode* p;
		p = adjList[i].firstEdge;
		while (p)
		{
			cout << p->adivex << "——";
			p = p->next;
		}
		cout << "NULL" << endl;
	}
}

image-20211125132546149

image-20211125133231818

image-20211125133156493

image-20211125133440575

空间性能 时间性能 适用范围 唯一性
邻接矩阵 O$(n^2)$ O$(n^2)$ 稠密表 唯一
邻接表 O(n+e) O(n+e) 稀疏表 不唯一

image-20211125135412611

#include<iostream>
using namespace std;

class MGraph;
class ALGraph;

void cinij(int& vi, int& vj)
{
	cout << "请输入该边依附的顶点编号" << endl;
	cin >> vi >> vj;
}


//无向图的邻接矩阵
#define DataType int
const int MAX_VERTEX = 10;//图的最大顶点数
class MGraph
{
public:
	MGraph();
	MGraph(DataType v[],int n,int e);
	~MGraph();
	void DFSTraverse(int v);//深度优先遍历
	void BFSTraverse(int v);//广度优先遍历
	void display();//打印邻接矩阵和顶点数组
	friend void change(MGraph& a, ALGraph& b);//邻接矩阵转换为邻接表
	friend void change(ALGraph& a, MGraph& b);//邻接表转邻接矩阵
	friend void print(MGraph &a,ALGraph &b);
private:
	DataType vertex[MAX_VERTEX];//顶点数组
	int arc[MAX_VERTEX][MAX_VERTEX];//边
	int vettexNum, arcNum;//实际定点数和边数
};

//析构函数
MGraph::MGraph()
{
	vettexNum = 0;
	arcNum = 0;
	for (int i = 0; i < MAX_VERTEX; i++)
	{
		vertex[i] = 0;//顶点数组初始化
	}
	for (int i = 0; i < MAX_VERTEX; i++)
	{
		for (int j = 0; j < MAX_VERTEX; j++)
		{
			arc[i][j] = 0;//初始化邻接矩阵
		}
	}
}
MGraph::MGraph(DataType v[],int n,int e)
{
	vettexNum = n;
	arcNum = e;
	for (int i = 0; i < vettexNum; i++)
	{
		vertex[i] = v[i];//顶点数组初始化
	}
	for (int i = 0; i < vettexNum; i++)
	{
		for (int j = 0; j <vettexNum; j++)
		{
			arc[i][j] = 0;//初始化邻接矩阵
		}
	}
	for (int i = 0; i < arcNum; i++)
	{
		//依次输入每一条边
		int vi, vj;
		cinij(vi, vj);//输入边依附的顶点编号
		arc[vi][vj] = 1;//置有边标志
		arc[vj][vi] = 1;
	}

}

MGraph::~MGraph()
{
}

void MGraph::display()
{
	cout << "顶点数组为：" << endl;
	for (int i = 0; i < vettexNum; i++)
	{
		cout << vertex[i] << " ";
	}
	cout << endl;//打印顶点数组
	cout << "arc=" << endl;
	cout << " ";
	for (int i = 0; i < vettexNum; i++)
	{
		cout << " " << i;
	}
	cout << endl;//打印邻接矩阵
	for (int i = 0; i <vettexNum; i++)
	{
		cout << i << " ";
		for (int j = 0; j < vettexNum; j++)
		{
			cout << arc[i][j] << " ";
		}
		cout << endl;
	}

}
//邻接表存储有向图
//边表
typedef struct AdjVexNode
{
	int adivex;//邻接点域，变得终点在定点表中的下标
	struct AdjVexNode* next;//指针域，指向边表中的下一个结点
}ArcNode;
//定点表
typedef struct Vettexnode
{
	DataType vettex;//数据源，存放顶点信息
	ArcNode* firstEdge;//指针域，指向边表中的第一个节点
}VettexNode;
class ALGraph
{
public:
	ALGraph(DataType v[],int n,int e);
	ALGraph();
	~ALGraph();
	void display();
	friend void change(MGraph& a, ALGraph& b);//邻接矩阵转换为邻接表
	friend void change(ALGraph& a, MGraph& b);//邻接表转邻接矩阵

private:
	VettexNode adjList[MAX_VERTEX];//定点表结构体数组
	int vertexNum, arcNum;//顶点个数，边的个数
};

ALGraph::ALGraph()
{
	vertexNum = 0;
	arcNum = 0;
	for (int i = 0; i < MAX_VERTEX; i++)
	{
		adjList[i].vettex = 0;
		adjList[i].firstEdge = NULL;
	}
}
ALGraph::ALGraph(DataType v[],int n,int e)
{
	vertexNum = n;
	arcNum = e;
	for (int i = 0; i < vertexNum; i++)
	{//输入定点信息，初始化定点表
		adjList[i].vettex = v[i];
		adjList[i].firstEdge = NULL;
	}
	//输入边的信息存储在边表中
	for (int i = 0; i < arcNum; i++)
	{
		int vi, vj;
		cinij(vi, vj);
		ArcNode *s = new ArcNode;
		s->adivex = vj;
		s->next = adjList[vi].firstEdge;
		adjList[vi].firstEdge = s;
	}
}

ALGraph::~ALGraph()
{
	for (int i = 0; i < vertexNum ;i++)
	{
		ArcNode* p;
		while (adjList[i].firstEdge)
		{
			p = adjList[i].firstEdge;
			adjList[i].firstEdge = adjList[i].firstEdge->next;
			delete p;
		}
	}
}

void ALGraph::display()
{
	for (int i = 0; i < vertexNum; i++)
	{
		cout << adjList[i].vettex << "——";
		ArcNode* p;
		p = adjList[i].firstEdge;
		while (p)
		{
			cout << p->adivex << "——";
			p = p->next;
		}
		cout << "NULL" << endl;
	}
}

void change(MGraph& a, ALGraph& b)
{
	b.vertexNum = a.vettexNum;
	b.arcNum = a.arcNum;
	for (int i = 0; i < a.vettexNum; i++)
	{
		b.adjList[i].vettex = a.vertex[i];
		b.adjList[i].firstEdge = NULL;
		for (int j = 0; j < a.vettexNum; j++)
		{
			if (a.arc[i][j])//&&i<j
			{
				ArcNode* s = new ArcNode;
				s->adivex = j;
				s->next = b.adjList[i].firstEdge;
				b.adjList[i].firstEdge = s;
			}
		}
	}
}
void change(ALGraph& a, MGraph& b)
{
	b.vettexNum = a.vertexNum;
	b.arcNum = a.arcNum;
	for (int i = 0; i < a.vertexNum; i++)
	{
		b.vertex[i] = a.adjList[i].vettex;
		ArcNode* p;
		p = a.adjList[i].firstEdge;
		while (p)
		{
			b.arc[i][p->adivex] = 1;
			//b.arc[p->adivex][i] = 1;
			p = p->next;
		}
	}
}



int main()
{
	int a[] = { 0,1,2,3 };
	ALGraph m;
	MGraph b(a,4,4);
	b.display();
	change(b, m);
	m.display();
}

4.图的遍历

image-20211125151949406

image-20211125152023304

image-20211125152135903

1.深度优先遍历

image-20211125152226032

伪代码：

从顶点v出发

1.访问顶点v;visited[v]=1;

2.w=顶点v的第一个邻接点

3.while（w）存在

3.1 if（w未被访问）从顶点w出发递归执行算法

3.2 w=顶点w的下一个邻接点

void MGraph::DFSTraverse(int v)
{
	static int visited[MAX_VERTEX] = { 0 };
	//初始化visite数组为0,(注意此数组的特殊性）
	cout << vertex[v] << "  ";//输出访问的节点信息
	visited[v] = 1;//将v标志为已访问
	for (int i = 0; i <vettexNum; i++)//j将v的邻接点访问一遍
	{
		if (arc[v][i] == 1 && visited[i] == 0)
		{
			DFSTraverse(i);//递归访问每个邻接点
		}
	}
}
void ALGraph::DFSTraverse(int v)
{
	//此函数有bug，当输入的结点只有出度为0时，无法进行遍历
	static int visited[MAX_VERTEX] = { 0 };
	//初始化visited数组为0
	cout << adjList[v].vettex << "  ";
	//输出访问过的结点
	visited[v] = 1;
	ArcNode* p;
	p = adjList[v].firstEdge;//工作指针p指向顶点v的边表
	while (p)
	{//用工作指针p依次搜索顶点v的邻接点，如果为被访问，则递归调用此函数
		if (visited[p->adivex] == 0)
		{
			DFSTraverse(p->adivex);
		}
		p = p->next;
	}
}
2.广度优先遍历

image-20211125224135789

伪代码：

1.初始化队列Q；

2.访问顶点v，visisted[v]=1;顶点v入队

3.while（队列Q非空）

3.1 v=队列Q的对头元素出队

3.2 w=顶点v的第一个邻接点

3.3 while（w存在）

3.3.1 如果w未被访问，则访问顶点w；visited[w]=1，顶点w入队

3.3.2 w=顶点的下一个邻接点

void MGraph::BFSTraverse(int v)//BFS遍历
{
	int visisted[MAX_VERTEX] = { 0 };//初始化visited数组
	cout << vertex[v] << " ";//输出访问过的顶点信息
	visisted[v] = 1;
	queue<int> q;//定义队列数组Q
	q.push(v);//对头元素入队
	while (!q.empty())
	{
		//当队列非空
		int v;
		v = q.front();//将丢头元素出队并送到v
		q.pop();
		for (int i = 0; i < vettexNum; i++)
		{
			//将所有顶点扫描一遍
			if (arc[v][i] != 0 && visisted[i] == 0)
			{
				cout << vertex[i] << " ";
				visisted[i] = 1;
				q.push(i);//将w入队
			}
		}
	}
}
void ALGraph::BFSTraverse(int v)
{
	//初始化visisted数组
	int visited[MAX_VERTEX] = { 0 };
	//访问首元素
	cout << adjList[v].vettex << " ";
	visited[v] = 1;//加访问标志
	queue<int> q;//定义队列Q
	q.push(v);//队头元素入队
	while (!q.empty())
	{//当队列非空时
		int v;
		v = q.front();
		q.pop();//队头元素出队，存入v中
		ArcNode* p;//工作指针p指向顶点v的边表
		p = adjList[v].firstEdge;
		while (p)
		{//如果v为被访问，则访问顶点w，visisted[w]=1,顶点w入队
			if (visited[p->adivex] == 0)
			{
				cout << adjList[p->adivex].vettex << " ";
				visited[p->adivex] = 1;
				q.push(p->adivex);
			}
			p = p->next;
			//p指向顶点v的下一个邻接点
		}
	}
}

5.最小生成树

1.Prim算法

image-20211130100109799

image-20211130101724698

image-20211130101927557

image-20211130102107447

image-20211130104754454

image-20211130110409523

image-20211130111621387

image-20211130111648432

int minEdge(ShortEdge* shortEdge, int vertNum)//寻找最小短边的邻接点k
{
	int temp;
	int k;
	for (int i = 0; i < vertNum; i++)
	{
		if (shortEdge[i].lowcost == 0) continue;
		else
		{
			temp = shortEdge[i].lowcost;
			k = i;
			break;
		}
	}
	for (int i = 0; i < vertNum; i++)
	{
		if (shortEdge[i].lowcost == 0) continue;
		else
		{
			if (temp > shortEdge[i].lowcost)
			{
				temp = shortEdge[i].lowcost;
				k = i;
			}
		}
	}
	return k;
}
void outputMST(AMGraph &G, int k, ShortEdge shortEdge)
{

	cout << "(" <<G.vertex[shortEdge.vertex] << "," << G.vertex[k] << ")" << shortEdge.lowcost << endl;
}
void Prime(AMGraph& G, int start)
{
	int vertexNum = G.getvertexNum();
	ShortEdge* shortEdge = new ShortEdge[vertexNum];
	for (int i = 0; i < vertexNum; i++)//初始化辅助数组shortEdge
	{
		shortEdge[i].lowcost = G.arc[start][i];
		//cout << G.arc[start][i] << endl;
		shortEdge[i].vertex = start;
	}
	shortEdge[start].lowcost = 0;//将起点start放入集合U
	/*for (int i = 0; i < vertexNum; i++)
	{
		cout << shortEdge[i].vertex << "   " << shortEdge[i].lowcost << endl;
	}*/
	for (int i = 0; i < G.vertexNum-1; i++)
	{
		int k = minEdge(shortEdge, vertexNum);////寻找最短边的邻接点k
		//cout << "k=" << k << endl;
		outputMST(G,k, shortEdge[k]);//输出最小生成树路径
		shortEdge[k].lowcost = 0;//将顶点k加入到集合U中
		for (int j = 0; j < vertexNum; j++)//调整数组shortEdge[n]
		{
			if (G.arc[k][j] < shortEdge[j].lowcost)
			{
				shortEdge[j].lowcost = G.arc[k][j];
				shortEdge[j].vertex = k;
			}
		}
		/*for (int i = 0; i < vertexNum; i++)
		{
			cout << shortEdge[i].vertex << "   " << shortEdge[i].lowcost << endl;
		}*/
	}
}
2.Kruskal算法

image-20211125162922423

image-20211125163200144

伪代码：

1.初始化：U=V；TE={}；

2.重复下述操作直到T中联通分支个数为1：

2.1.在E中寻找最短边（u，v);

2.2. 如果u，v位于T的两个不同联通分量，则：

2.2.1将边（u，v)并入TE；

2.2.2 将这两个联通分量合为一个；

2.3.标记边（u，v)，使得（u，v)不参与后续最短边的选取

image-20211125165731908

image-20211125165810224

image-20211125171321963

image-20211125171350452

6.最短路径

1.Dijskra

在非网图中，最短路径是指两顶点之间经历的边数最少的路径

在网图中，最短路径是指两顶点之间经历的便是权值和最小的路径

image-20211201220617965

image-20211201222148074

image-20211201222222446

image-20211201223657623

image-20211201224014343

image-20211201224127697

image-20211201224753620

image-20211201224401934

//找出dist中查找s[i]==0的最小元素值
int finMinDist(int dist[], int s[], int vertexNum)
{
	int min;
	int k;
	for (int i = 0; i < vertexNum; i++)
	{
		if (s[i] == 1)
		{
			continue;
		}
		else
		{
			min = dist[i];
			k = i;
			break;
		}

	}
	for (int i = 0; i < vertexNum; i++)
	{
		if (s[i] == 0 && min > dist[i])
		{
			min = dist[i];
			k = i;
		}
	}
	return k;
}

void display(int dist[], DataType path[], int startV, int vertexNum,DataType vertex[])
{
	for (int i = 0; i < vertexNum; i++)
	{
		cout << dist[i] << "    " << path[i] << endl;
	}
	for (int i = 1; i < vertexNum; i++)
	{
		stack<int> s;
		s.push(i);
		int a = path[i];
		s.push(a);
		while (a!=startV)
		{
			a = path[a];
			s.push(a);
		}
		cout << vertex[startV] << "->" << vertex[i]<<"的最短路径为: ";
		while (!s.empty())
		{
			cout << vertex[s.top()] << "   ";
			s.pop();
		}
		cout << "最短路径长度为;"<<dist[i] << endl;
	}
}

/*参数G传入图对象，v为计算的起点*/
void Dijkstra(AMGraph& G, int startV)
{
	int* path = new int[G.vertexNum];
	int* dist = new int[G.vertexNum];
	int* s = new int[G.vertexNum];
	for (int i = 0; i <G.vertexNum; i++)
	{
		s[i] = 0;//初始化集合s，初始化为0
	}
	s[startV] = 1;//将起始顶点放入集合s中，1，代表在集合中，0代表不在集合s中
	for (int i = 0; i < G.vertexNum; i++)
	{
		dist[i] = G.arc[startV][i];//初始化dist数组
		if(dist[i]!=MaxInt)
		{
			path[i] = startV;//初始化path数组
		}
		else
		{
			path[i] = -1;
		}
	}
	int num = 1;//代表集合s中的顶点个数
	while (num<G.vertexNum)
	{
		int min;
		//dist中查找s[i]为0的最小值
		min = finMinDist(dist, s, G.vertexNum);
		s[min] = 1;//将新生成的最小终点加入到集合s
		for (int i = 0; i < G.vertexNum; i++)
		{//修改数组dist和path
			if (s[i] == 0 && (dist[i] > dist[min] + G.arc[min][i]))
			{
				//用以找到的最短路径修改对应的dist
				dist[i] = dist[min] + G.arc[min][i];
				path[i] = min;//用以找到的最短路径修改path
			}
		}
		num++;
	}
	display(dist, path, startV, G.vertexNum,G.vertex);
}





/*请输入结点个数和边个数：
5 7 1 2 3 4 5 1 2 10 1 4 30 2 3 50  3 5 10 4 3 20 4 5 60 5 1 100
请输入顶点
请输入第0条边的顶点和信息
请输入第1条边的顶点和信息
请输入第2条边的顶点和信息
请输入第3条边的顶点和信息
请输入第4条边的顶点和信息
请输入第5条边的顶点和信息
请输入第6条边的顶点和信息
顶点数组为：
1 2 3 4 5
arc=
  0 1 2 3 4
0 0 10 --30 --
1 --0 50 ----
2 ----0 --10
3 ----20 0 60
4 100 ------0
请输入起点:0
0    0
10    0
50    3
30    0
60    2
1->2的最短路径为: 1   2   最短路径长度为;10
1->3的最短路径为: 1   4   3   最短路径长度为;50
1->4的最短路径为: 1   4   最短路径长度为;30
1->5的最短路径为: 1   4   3   5   最短路径长度为;60*/
2.Floyd

image-20211202150124542

image-20211202150158075

image-20211202150220680

image-20211202150437326

image-20211202153810820

image-20211202154527266

image-20211202154625454

image-20211202160116937

image-20211202160151939

有向无环图及其应用

1.AOV(拓扑排序)

20211202174526

20211202174543

IMG_20211202_174906

20211202174959

20211202175244

拓扑排序使得AOV网中所有应存在前驱和后继的关系都能得到满足 20211202175527

2.AOE（关键路径）

20211202162428

20211202162907

20211202163448

20211202163508

20211202163747

20211202164050

20211202164926

20211202165500

==关键路径==：活动最早开始时间和最晚开始时间相等的事件

20211202165835

20211202172246

IMG_20211202_172431

20211202172947

20211202173246

20211202173306

常见问题

1.gcc中文乱码

g++ -fexec-charset=GBK main.cpp -o main.exe && main.exe

-fexec-charset=charset，此选项指定窄字符或窄字符串的字面值常量的内部编码方式，默认为UTF-8。例如指定此选项为GBK，则窄字符或窄字符串常量将会以GBK编码方式存储而不是默认的UTF-8编码方式。

2.输出结果打印的文件中

./a+(空格)+>(空格)文件名

3.gcc 汇编代码

gcc 1.c --save-temps   //保存所有编译中生成的文件

gcc -O2 -S 1.c  // 直接生成汇编文件
4.linux常用命令

关机 init 0 或halt

重启 init 6 或reboot

时间操作: date 查看时间

修改时间  date -s "2021-09-11 14:21:21"

设置时区为上海cp /usr/share/zoneinfo/Asia/Shanghai /etc/localtime

复制 ctrl+insert 粘贴 shift+insert

ctrl +c 停止命令

pwd 查看当前目录

cd

cd ..上一级目录

ls -l 列出目录和文件的详细信息

ls -lt 列出目录和文件的详细信息，按时间降序显示。

传输文件

sftp [email protected]

put 文件名

正则表达式

? 只匹配一个字符

解压文件 tar zxvf +文件名

About

data structure code

Resources

Readme
Activity

Stars

0 stars

Watchers

2 watching

Forks

0 forks
Report repository

Releases

No releases published

Packages

No packages published

Languages