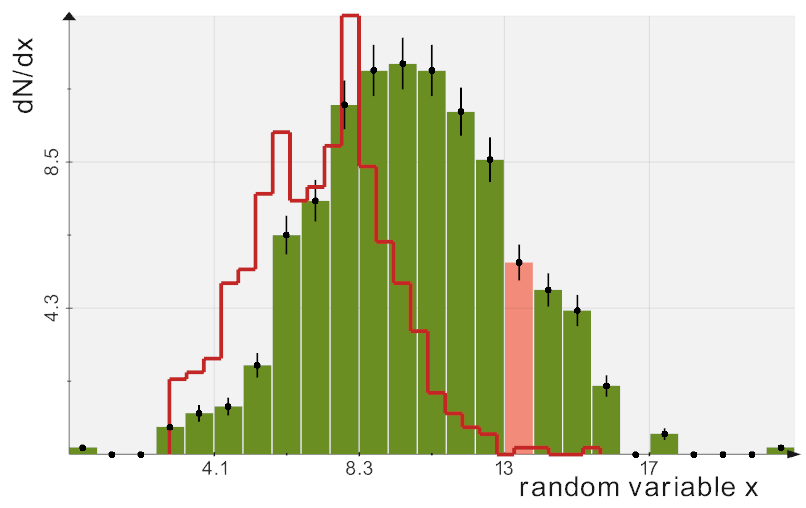
A lightweight pure python module for scientific analysis and visualization of 3D objects and point clouds based on VTK and numpy.

(click on the picture to open a 3D viewer)

✨ Philosophy

Inspired by the vpython manifesto "3D programming for ordinary mortals", vtkplotter makes it easy to work wth three-dimensional objects, create displays and animations in just a few lines of code, even for those with less programming experience.

🎯 Table of Contents

• Installation
• Documentation
• Features
• Command Line Interface
• Examples Gallery
• References

💾 Installation

Use pip to install:

pip install -U vtkplotter

or use conda to install from the conda-forge channel:

conda install -c conda-forge vtkplotter

or on Ubuntu OS:

sudo apt install python3-vtkplotter

Windows-10 users can place this file vtkplotter.bat on the desktop to drag&drop files to visualize. (Need to edit the path of the local python installation).

📙 Documentation

Automatically generated documentation can be found here.

📌 Need help? Have any question, or wish to suggest or ask for a missing feature? Do not hesitate to open a issue or send an email.

🎨 Features

Intuitive and straightforward API which can be combined with VTK seamlessly in a program, whilst mantaining access to the full range of VTK native classes.

It includes a large set of working examples for a wide range of functionalities:

working with polygonal meshes and point clouds *[click triangle to expand]*

- Import meshes from VTK format, STL, Wavefront OBJ, 3DS, Dolfin-XML, Neutral, GMSH, OFF, PCD (PointCloud),

- Export meshes as ASCII or binary to VTK, STL, OBJ, PLY ... formats.

- Analysis tools like Moving Least Squares, mesh morphing and more..

- Tools to visualize and edit meshes (cutting a mesh with another mesh, slicing, normalizing, moving vertex positions, etc..).

- Split mesh based on surface connectivity. Extract the largest connected area.

- Calculate areas, volumes, center of mass, average sizes etc.

- Calculate vertex and face normals, curvatures, feature edges. Fill mesh holes.

- Subdivide faces of a mesh, increasing the number of vertex points. Mesh simplification.

- Coloring and thresholding of meshes based on associated scalar or vectorial data.

- Point-surface operations: find nearest points, determine if a point lies inside or outside of a mesh.

- Create primitive shapes: spheres, arrows, cubes, torus, ellipsoids...

- Generate glyphs (associate a mesh to every vertex of a source mesh).

- Create animations easily by just setting the position of the displayed objects in the 3D scene. Add trailing lines and shadows to moving objects is supported.

- Straightforward support for multiple sync-ed or independent renderers in  the same window.

- Registration (alignment) of meshes with different techniques.

- Mesh smoothing.

- Delaunay triangulation in 2D and 3D.

- Generate meshes by joining nearby lines in space.

- Find the closest path from one point to another, travelling along the edges of a mesh.

- Find the intersection of a mesh with lines, planes or other meshes.

- Interpolate scalar and vectorial fields with Radial Basis Functions and Thin Plate Splines.

- Add sliders and buttons to interact with the scene and the individual objects.

- Visualization of tensors.

- Analysis of Point Clouds:

 - Moving Least Squares smoothing of 2D, 3D and 4D clouds

 - Fit lines, planes, spheres and ellipses in space

 - Identify outliers in a distribution of points

 - Decimate a cloud to a uniform distribution.

working with volumetric data, and tetrahedral meshes

- Import data from VTK format volumetric TIFF stacks, DICOM, SLC, MHD and more

- Import 2D images as PNG, JPEG, BMP

- Isosurfacing of volumes

- Composite and maximum projection volumetric rendering

- Generate volumetric signed-distance data from an input surface mesh

- Probe a volume with lines and planes

- Generate stream-lines and stream-tubes from vectorial fields

- Slice and crop volumes

- Support for other volumetric structures (structured and grid data)

plotting and histogramming

- Fully customizable axis styles

- 'donut' plots and pie charts

- Scatter plots in 2D and 3D

- Surface function plotting

- 1D customizable histograms

- 2D hexagonal histograms

- Polar plots, spherical plots and histogramming

- Draw latex-formatted formulas in the rendering window.

- Quiver plots

- Stream line plots

- Point markers analogous to matplotlib

Moreover:

• Integration with the Qt5 framework.
• Examples using SHTools package for spherical harmonics expansion of a mesh shape.
• Support for FEniCS/Dolfin platform for visualization of finite-element calculations.
• Interoperability with the trimesh library.
• Export a 3D scene and embed it into a web page.
• Embed the 3D rendering in a jupyter notebook with K3D (can export an interactive 3D-snapshot page here).

⌨ Command Line Interface

Visualize a polygonal mesh from a terminal window with:

vtkplotter mesh.obj
# valid formats: [vtk,vtu,vts,vtp,vtm,ply,obj,stl,3ds,dolfin-xml,neutral,gmsh,
#                 pcd,xyz,txt,byu,tif,off,slc,vti,mhd,dcm,dem,nrrd,nii,bmp,png,jpg]

Volumetric files (mhd, vti, slc, tiff, DICOM etc..) can be visualized with options:

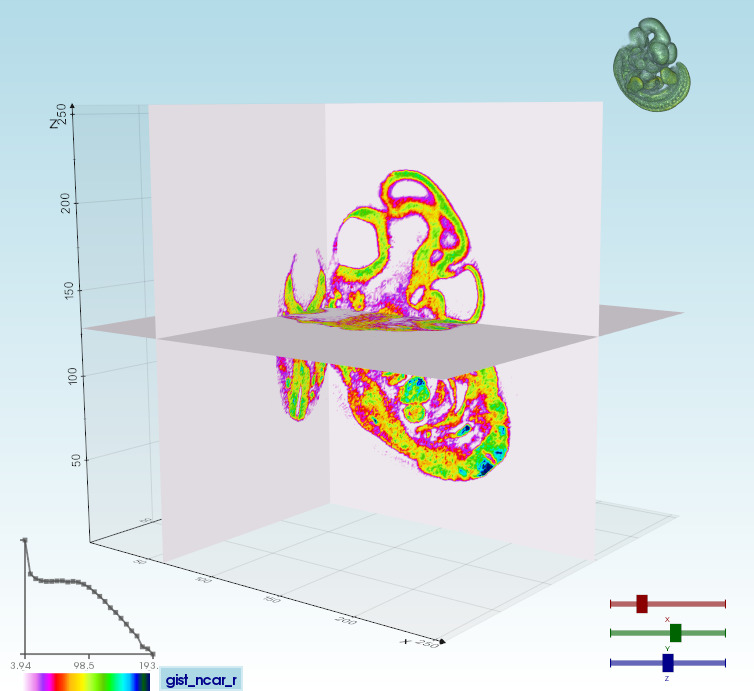
Slice a volume in the 3 planes: vtkplotter --slicer embryo.slc	Ray-casting rendering: -g embryo.slc	2D slice: --slicer2d	Colorize voxels: --lego

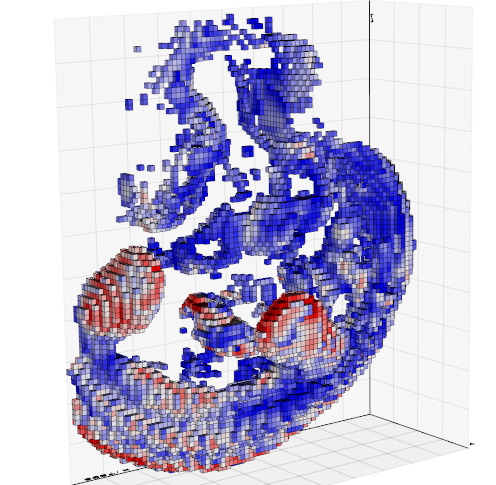To visualize multiple files or files time-sequences try -n or -s options. Use -h for the complete list of options.

A GUI is also available (mainly useful to Windows 10 users).

🐾 Examples

More than 300 working examples can be found in directories (scroll down to see thumbnails):
examples/basic
examples/advanced
examples/volumetric
examples/tetmesh
examples/simulations
examples/pyplot
examples/other
examples/other/dolfin
examples/other/trimesh
examples/notebooks

Apply a Moving Least Squares algorithm to obtain a smooth surface from a to a large cloud of scattered points in space (script)	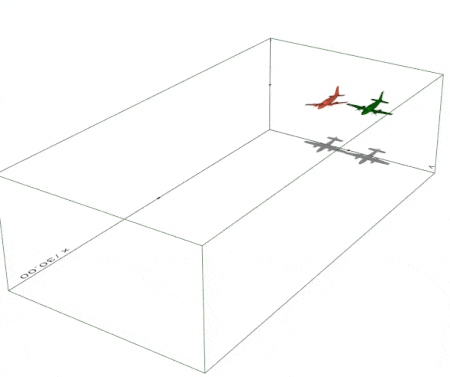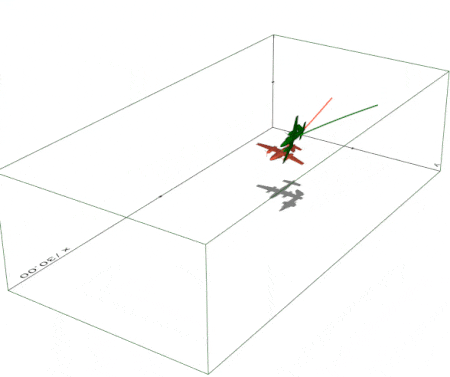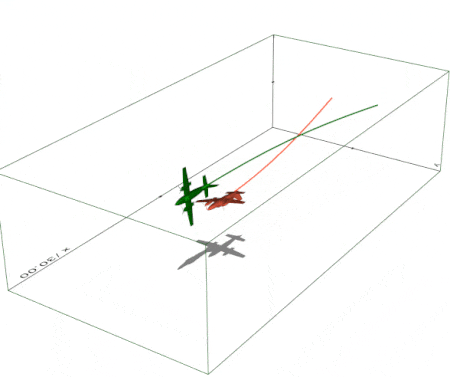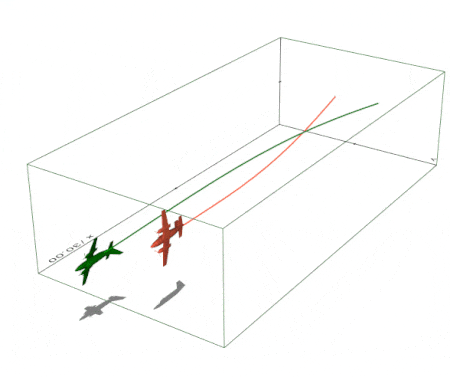Create a simple 3D animation in exactly 10 lines of code (script). Trails and shadows can be added to moving objects easily.
Simulation of a gyroscope hanging from a spring (script).	Quantum-tunnelling effect integrating the Schroedinger equation with 4th order Runge-Kutta method. The animation shows the evolution of a particle in a box hitting a sinusoidal potential barrier. (script)
Turing system of reaction-diffusion between two molecules (script)	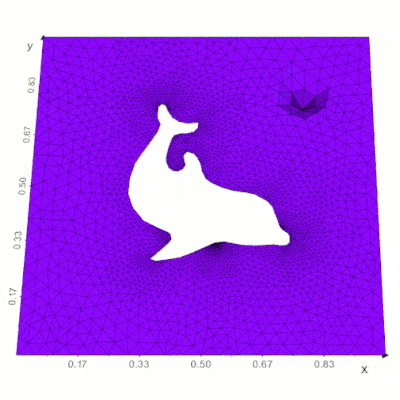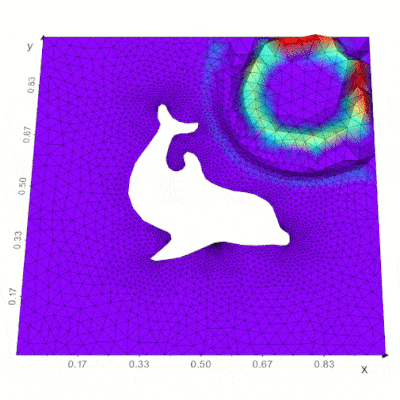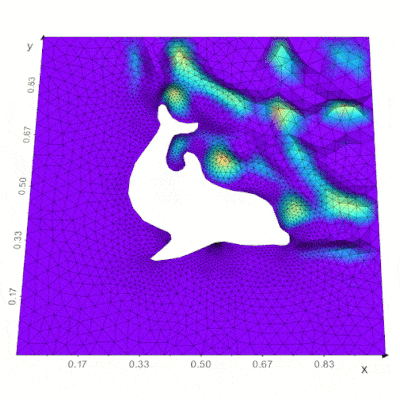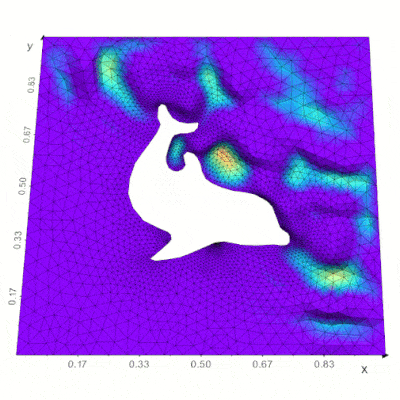Support for the FEniCS/Dolfin platform for visualization of PDE and finite element solutions (see here)

Random Gallery of Examples

Run any of the built-in examples from command line, e.g.:

vtkplotter -ir covid19

geological	multirender	cartoony	streamlines4
covid19	lineage_graph	silhouette1	isolines
gyroscope2	thinplate_grid	trail	quadratic_morphing
shrink	mesh_custom	spring	lorentz
sliders	fitspheres1	plot4_fxy	histo_1D
plot2_errband	histo_2D	histo_hexagonal	plot5_spheric
boolean	brownian2D	gas	self_org_maps2d
geodesic	convexHull	flatarrow	latex
legosurface	streamlines2	office.py	value-iteration
shadow	multiple_pend	interpolateVolume	histo_polar
plot7_stream	histo_violin	plot3_pip	histo_spheric
read_vts	donut	extrude	plot1_errbars
particle_simulator	heatconv	elastodynamics	stokes_lshape

📜 References

• M. Musy, G. Dalmasso, J. Sharpe and N. Sime, "vtkplotter: plotting in FEniCS with python", (link). Poster at the FEniCS'2019 Conference, Carnegie Institution for Science Department of Terrestrial Magnetism, Washington DC, June 2019.

• G. Dalmasso, "Evolution in space and time of 3D volumetric images". Talk at the Conference for Image-based Modeling and Simulation of Morphogenesis. Max Planck Institute for the Physics of Complex Systems, Dresden, Germany, March 2019.

Scientific publications using vtkplotter so far:

1. X. Diego et al.: "Key features of Turing systems are determined purely by network topology", Physical Review X, 20 June 2018.
2. M. Musy, K. Flaherty et al.: "A Quantitative Method for Staging Mouse Limb Embryos based on Limb Morphometry", Development, 5 April 2018, doi: 10.1242/dev.154856.
3. G. Dalmasso et al., "Evolution in space and time of 3D volumetric images", in preparation.
4. F. Claudi, A. L. Tyson, T. Branco, "Brainrender. A python based software for visualisation of neuroanatomical and morphological data." bioRxiv 2020.02.23.961748; doi: https://doi.org/10.1101/2020.02.23.961748

Have you found this software useful for your research? Please cite it as:
M. Musy et al. "vtkplotter, a python module for scientific visualization and analysis of 3D objects and point clouds based on VTK (Visualization Toolkit)", Zenodo, 10 February 2019, doi: 10.5281/zenodo.2561402.