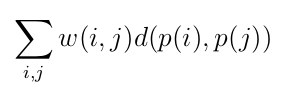Repositorio creado para la asignatura de Inteligencia Computacional en el máster de ingeniería informática en Granada
El objetivo de esta práctica es resolver un problema de optimización tı́pico utilizando técnicas de computación evolutiva. Deberá implementar varias variantes de algoritmos evolutivos para resolver el problema de la asignación cuadrática, incluyendo como mı́nimo las variantes que se describen en este guión de prácticas.
El objetivo de esta práctica es resolver un problema de optimización típico utilizando técnicas de computación evolutiva. Para ello se van a implementar varias versiones o variantes sobre los algoritmos evolutivos para resolver el problema de la asignación cuadrática, incluyendo las variantes de:
- Algoritmo genético sin optimización local.
- Algoritmo genético con variante lamarckiana.
- Algoritmo genético con variante baldwidiana.
En este estudio, se analizarán las diferencias y rendimientos obtenidos con cada una de estar variantes, y se proporcionará un resultado de coste calculado para el conjunto de datos llamados “tai256c.dat”.
Las pruebas del algoritmo evolutivo han sido ejecutadas con el siguiente hardware y sistema operativo:
- Procesador: Intel(R) Core(TM) i5-8250U CPU @1.60GHz 1.80GHz
- Memoria RAM: 8,00 GB
- Tarjeta gráfica: NVIDIA GeForce MX150.
Para desarrollar el software necesario se ha utilizado lo siguiente:
- Lenguaje programación: C++
- Sistema operativo: Ubuntu 18.04
- IDE: Qt creator
- Frameworks y librerías: En este caso no se ha utilizado ninguna librería ni framework externo, sino que se han utilizado las propias librerías estándar de C++
El problema de la asignación cuadrática o QAP [Quadratic Assignment Problem] es un problema fundamental de optimización combinatoria con numerosas aplicaciones. En este caso tenemos una serie de flujos, que en este documento va a ser tratado como fábricas, y una serie de posibles localizaciones donde van a ser ubicadas dichas fábricas.
Para esto, se conoce la distancia que hay entre cada una de las posibles localizaciones y el flujo de materiales que existe para cada fábrica.
Formalmente, si llamamos d(i, j) a la distancia de la localización i a la localización j y w(i; j) al peso asociado al flujo de materiales que ha de transportarse de la fábrica i a la fábrica j, hemos de encontrar la asignación de instalaciones a localizaciones que minimice la función de coste:
Donde p() define una permutación sobre el conjunto de fábricas.
En primer lugar, se va a representar la estructura de una posible solución del problema. Dicha estructura va a ser un vector donde cada posición va a representar a una unidad, y cada valor de dicha posición va a ser la localización.
Este vector ha sido incluido como atributo llamado “solutions” en una clase llamado
“Individual”. Dicha clase va a representar a lo que se correspondería con un individuo de la
población.
Tras esto, se ha creado una clase llamada “Data” para poder cargar los datos desde los
ficheros y que estos puedan ser tratados directamente desde nuestro algoritmo.
A continuación, se ha creado una clase llamada “Poblation”, con la que se va a modelar una población de individuos. Dicha población tendrá una serie de métodos asociados para trabajar con sus individuos.
Posteriormente se ha implementado una clase llamada "Optimizer” con la que se va a modelar los posibles algoritmos de optimización local que va a utilizar el algoritmo genético. En este caso se ha implementado un algoritmo de búsqueda local.
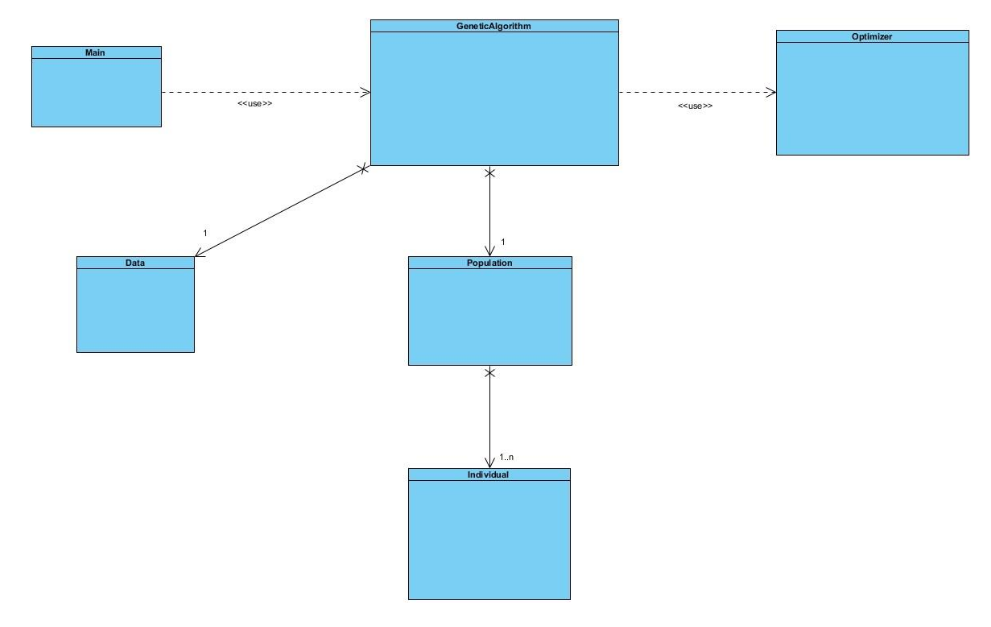
Por último, se ha diseñado la clase “GeneticAlgorithm” con la que se ha modelado el algoritmo genético. Esta clase es la principal de la aplicación y hace uso de todas las clases anteriores para su correcto funcionamiento. Esta clase contiene las variantes de los algoritmos (Lamarckiana, Baldwiniana y sin optimización local) junto con los operadores de selección cruce y mutación. Más adelante se detallará como se ha implementado cada uno de estos operadores.
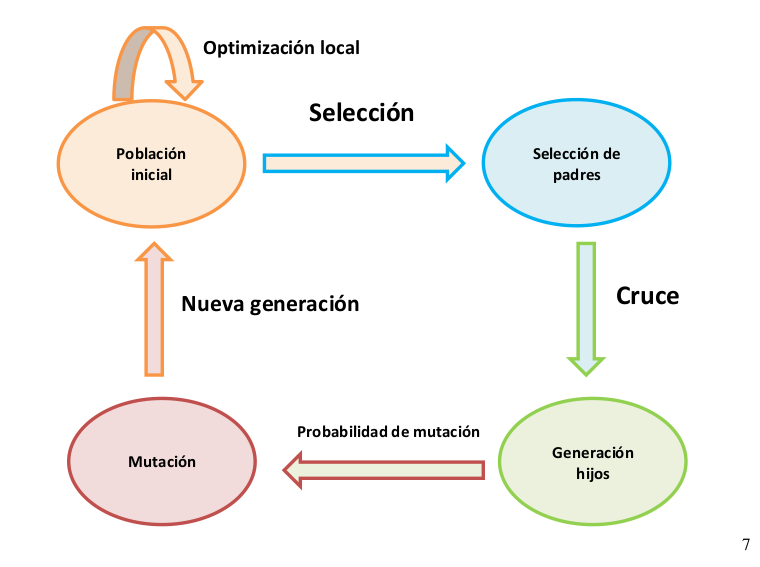
El modelo conceptual de la aplicación se resume en la siguiente figura:
En esta sección se va a describir las principales estrategias utilizadas para la realización del algoritmo genético.
La generación de individuos se ha realizado totalmente de forma aleatoria. Un individuo va a formar parte de una posible solución al problema, por ello vamos a calcular una primera solución de forma aleatoria
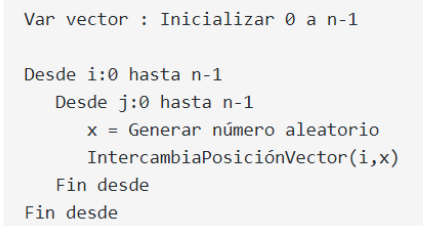
Cada individuo se generará inicialmente de la siguiente manera: Se parte con un vector totalmente inicializado desde 0 hasta n-1, y la idea es intercambiar las posiciones de forma aleatoria. El pseudocódigo es el siguiente:
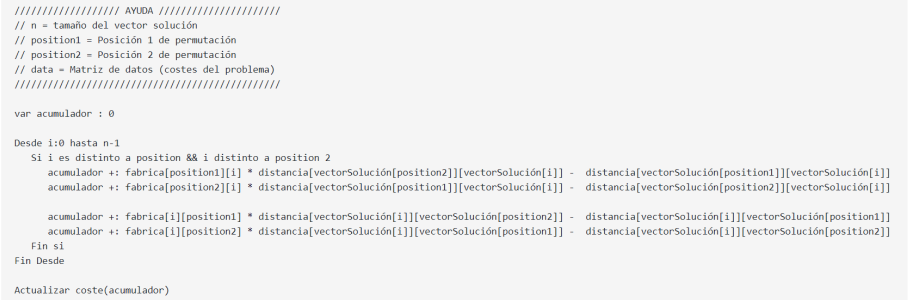
Cada individuo tendrá un coste asociado que se corresponderá con la bondad de la solución que representa. El cálculo de dicho coste se ha realizado de la siguiente forma:
Con el objetivo de no tener que volver a recalcular todo el coste de un individuo cuando permutan solo dos valores (coste computacionalmente alto), se ha realizado una nueva función para poder recalcular el coste, partiendo como base el coste actual y calculando la diferencia que supondría respecto al nuevo cambio (permutación).
Para la generación de las poblaciones se generan una serie de individuos aleatorios y se añaden a dicha población hasta completarla.
Para optimizar los individuos que inicialmente se generan en la población se ha utilizado una búsqueda local del mejor vecino. En este caso he seguido siguiente pseudocódigo[1] para realizar mi implementación:
Este algoritmo nos permitirá ir obteniendo una serie de generaciones de individuos que van evolucionando y mejorando las soluciones previamente obtenidas. El modelo de la población es de tipo generacional , es decir, cada individuo va a vivir durante una generación, ya que en la siguiente generación serán reemplazados.
Como se ha comentado anteriormente, se va a implementar una variante lamarckiana, balwidiana y sin utilizar optimización local. El proceso básico que va a generar este algoritmo en cada iteración es el siguiente:
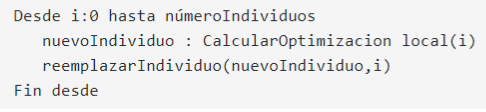
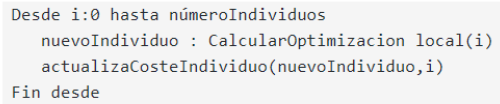
Tal y como se ha comentado anteriormente, la generación de individuos se genera de forma aleatoria en la primera iteración. Tras la obtención de dichos individuos se procede a optimizarlos utilizando un algoritmo de búsqueda local y aplicando los siguientes cambios según la variante del algoritmo que se utiliza:
-
Variante lamarckiana: Los nuevos individuos resultantes de la optimización local reemplazan al individuo de dicha población.
-
Variante balwidiana: Se calculan los individuos resultantes de la optimización local, pero en este caso no reemplazan al individuo de la población, sino que el coste de esos individuos resultantes se utilizarán posteriormente en la selección.
-
Variante sin optimización local: No se aplica el algoritmo de optimización local.
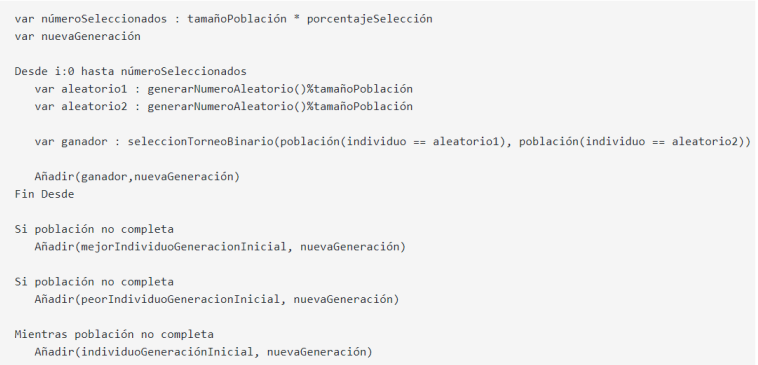
A la hora de realizar la selección de los individuos de la población inicial, para posteriormente convertirse en “padres” se tienen en cuenta dos factores:
-
El primer factor es un porcentaje de selección. Este es una variable del algoritmo que nos indica el porcentaje de individuos a los que se va a aplicar el operador de selección. El número restante de individuos es insertado directamente de la población inicial. Se añadirá el mejor individuo, el peor, y los mejores individuos restantes de la población (ordenada ascendentemente) hasta completar la población.
-
El segundo factor es la selección por torneo binario. Este es el operador que se ha utilizado para realizar la selección, en el que se enfrentan dos individuos escogidos de forma aleatoria y se devuelve el mejor individuo para que pase a formar parte de los “padres”.
Tal y como se ha comentado en el punto anterior, la generación de los padres es realizada mediante la selección por torneo binario y parte de los mejores y el peor individuo de la generación inicial. Todo este procedimiento se describe a continuación:
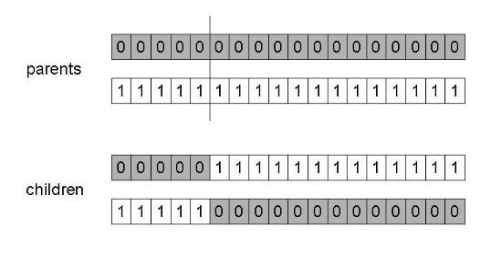
Una vez se ha generado la generación de padres, se procede a realizar un cruce entre ellos para generar a la nueva generación “hija”. El operador de cruce que se ha empleado es de tipo cruce en un punto , en el que se selecciona un punto de cruce aleatoriamente, se dividen los padres en ese punto y se crean los hijos intercambiando partes de los cromosomas. En la siguiente figura se muestra un ejemplo de este tipo de cruce:
En el proceso de cruce, se seleccionarán dos padres de forma aleatoria y darán lugar a dos hijos resultantes (como se puede observar en la figura anterior). Es importante destacar que una vez que un padre ha sido seleccionado, dicho padre no se volverá a combinar con ninguno más, es decir, un padre solo podrá “reproducirse” una sola vez.
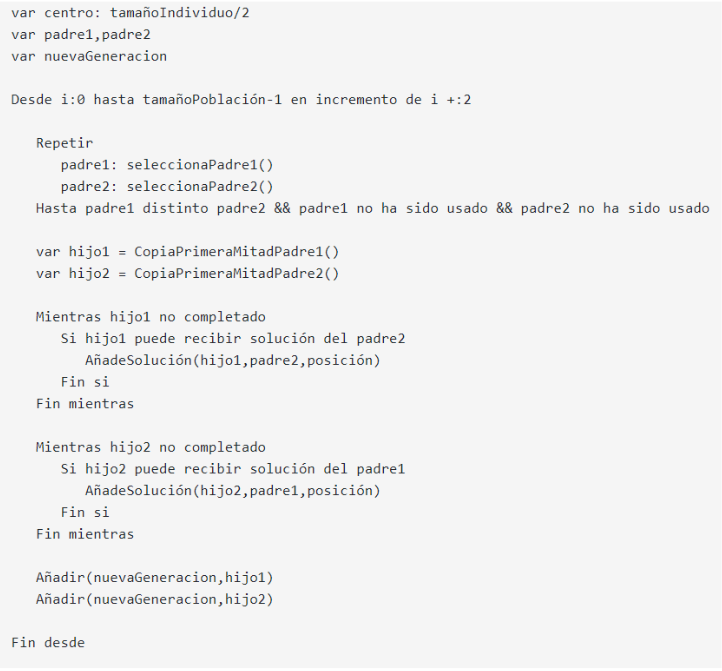
La generación de hijos es resultado de realizar un cruce de individuos entre la generación de los padres. A continuación se muestra un pseudocódigo de la versión que he implementado para llevar a cabo esta tarea.
Nota: El siguiente pseudocódigo no es exacto a la representación real. Se ha realizado de esta forma para simplificar el pseudocódigo, pero en el código real implementado se realiza todas las verificaciones necesarias para que el proceso se realice correctamente. Para más información se puede consultar el método correspondiente generateChildrenGeneration en el archivo de geneticAlgorithm.cpp
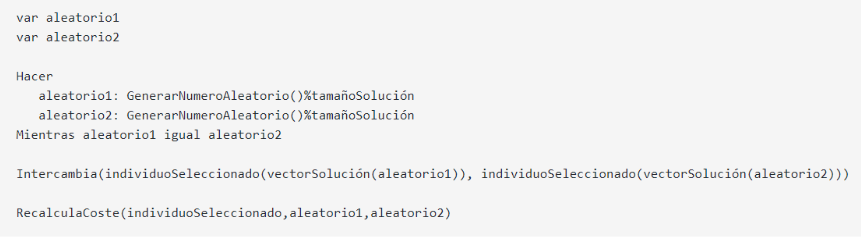
Una vez que se ha generado la población de hijos, es posible que algún individuo de dicha población pueda mutar. Esta posibilidad está basada en una probabilidad de mutación que es establecida en el algoritmo genético. Dicha mutación se calcula mediante un número aleatorio generado según la probabilidad de mutación. El operador que se ha utilizado para realizar la mutación es mediante intercambio. Su funcionamiento se describe en la siguiente figura.
El pseudocódigo de este algoritmo es el siguiente:
Tal y como se ha comentado en la introducción del punto 5 y haciendo un resumen en general, el proceso que sigue el algoritmo es la generación de una población inicial (lamarckiana, balwidiana o sin aplicar optimización local), posteriormente se selecciona y se generan unos padres que se cruzarán para dar a unos hijos, que tienen una probabilidad de mutar y dar lugar a una nueva generación.
Importante: En cada uno de estos procesos en el que se genera una nueva población, se realiza una comparación con el mejor individuo obtenido, actualizándose en el caso de que se haya mejorado.
El criterio de parada del algoritmo es un valor de n generaciones, ya que no se conoce el óptimo del problema que se quiere resolver.
A continuación se muestra el pseudocódigo correspondiente al proceso de evaluación según la variante (lamarkiana, baldwidiana o sin optimización local).
En esta sección se van a realizar las evaluaciones de las distintas variantes de los algoritmos, se realizará una comparación y finalmente se aportará la mejor solución obtenida para el problema propuesto llamado “tai256c.dat”
Para poder analizar el rendimiento de las variantes (balwidiana, lamarckiana y sin utilización de óptimo local), he realizado pruebas en conjuntos de datos más pequeños y he analizado los resultados obtenidos para obtener un análisis previo antes de ejecutar el algoritmo para el problema propuesto ya que tiene gran tamaño y su tiempo de ejecución es elevado.
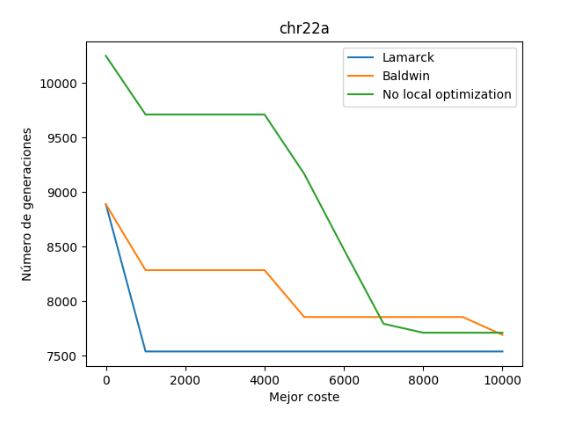
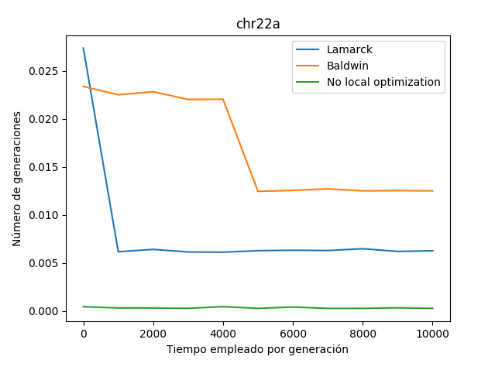
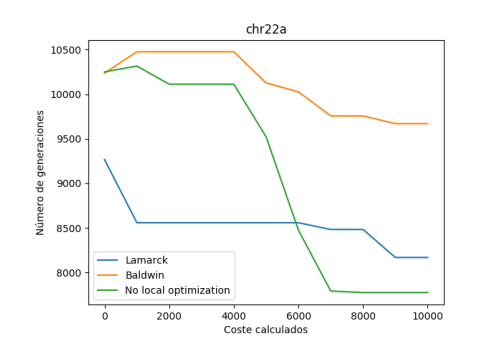
En primer lugar, se ha ejecutado el algoritmo con las 3 variantes para el conjunto de datos llamado “chr22a.dat” y se han obtenido los siguientes datos:
Empezamos analizando el mejor resultado obtenido para un número de generaciones de 10.000.
Como podemos observar, se ha obtenido un mejor resultado en la variante lamarckiana y como observación decir que en este caso de prueba para este número de ejecuciones, la variante baldwidiana y sin optimización local prácticamente han dado casi el mismo resultado. Posteriormente comprobaremos para otros ejemplos si esta situación sigue ocurriendo.
Respecto al tiempo empleado por generación, podemos observar que la variante balwidiana requiere de un mayor tiempo de ejecución que el resto, después le sigue la variante lamarckiana y por último sin optimización local (como es lógico).
Por último, respecto a la variación en los costes de cada generación, podemos observar que en la variante lamarckiana suele permanecer estable hasta que encuentra un coste menos elevado, y sigue esa misma línea sin volver a crecer.
Por otro lado, también podemos observar que en la variante balwidiana al principio el coste se eleva y luego desciende, pero no tiene punto de comparación con el de la variante lamarckiana.
Por último, tenemos la variante sin utilización de óptimo local, la cual vemos que siempre es decreciente.
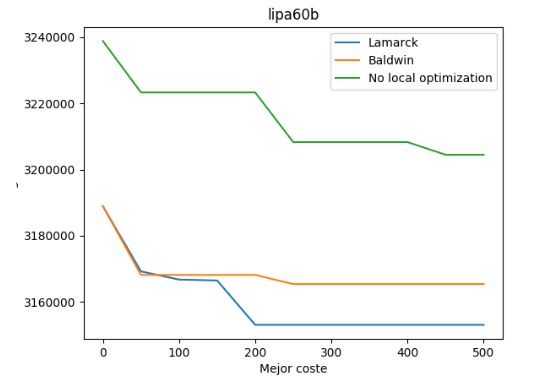
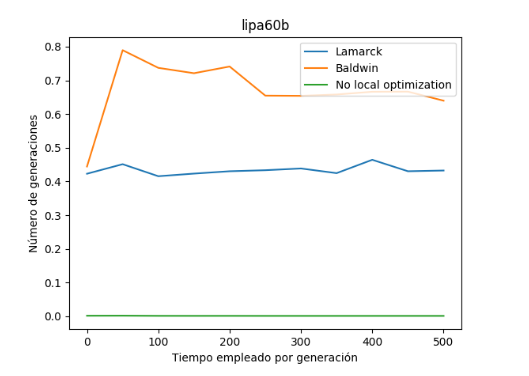
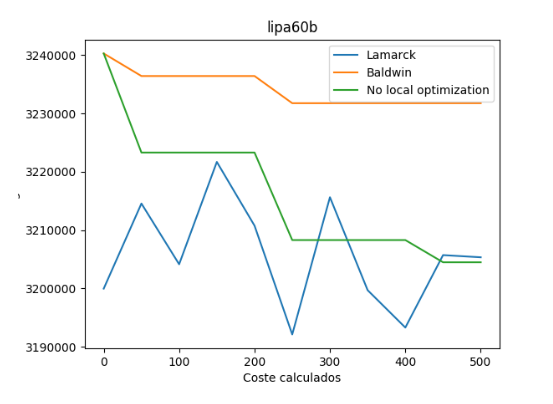
Ahora se va a analizar la misma información pero en este caso se ha escogido un conjunto de datos de mayor tamaño con un número de 500 generaciones. En concreto dicho conjunto de datos se llama “lipa60b”.
Como se puede observar, también la variante lamarckiana ha obtenido un mejor resultado que el resto.
Respecto al tiempo empleado para cada generación, se han obtenido los mismos resultados que para el conjunto de datos anterior, es decir, la variante que mayor tiempo emplea para una generación es la variante balwidiana seguida por la lamarckiana y por último por la variante sin óptimo local.
En este caso, podemos observar como hay una gran variación entre los costes calculados para cada generación en la variante lamarckiana (a gran diferencia del anterior caso). La variante balwidiana más o menos permanece estable y la variante sin optimización local es siempre decreciente.
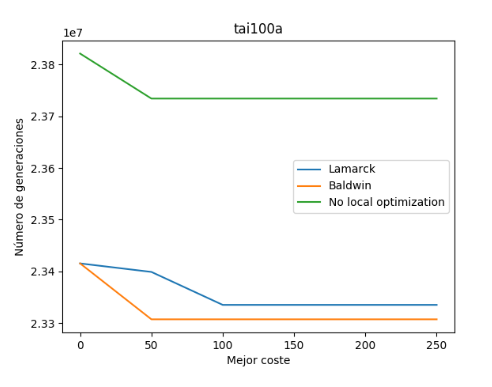
Por último en este análisis previo, se va a realizar las mismas pruebas para otro conjunto de datos más grande llamado “tai100a” para un número de 250 generaciones.
Observamos, que para este caso, la variante balwidiana ha dado un mejor resultado que el resto. A este tamaño y número de generaciones, podemos ver que la variante sin optimización local se queda bastante por atrás que las otras que si lo utilizan.
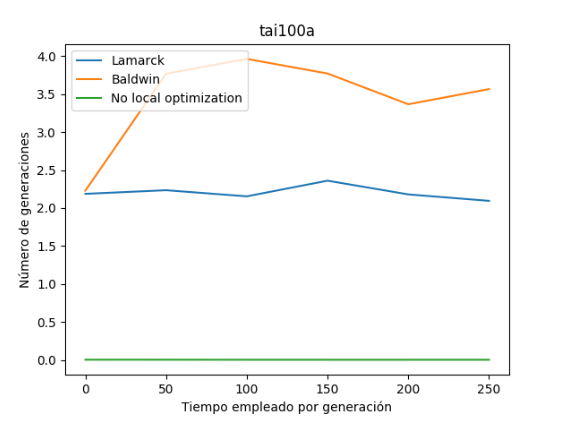
También observamos que el tiempo de ejecución entre las variantes sigue en la misma línea que el resto. La variante balwidiana es el que más tiempo emplea en cálculo de una nueva generación, seguido por la variante balwidiana y por último la variante sin optimización local.
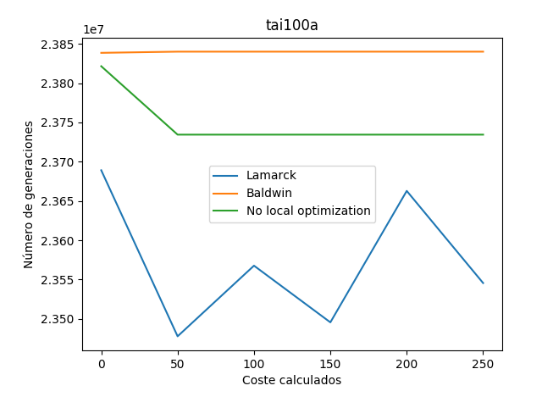
Finalmente, visualizamos que los costes de la variante balwidiana han permanecidos estables, y sin embargo los de la variante lamarckiana han ido oscilando creciente y decrecientemente.
Como conclusión de este análisis entre estas variantes, se puede deducir la siguiente información:
-
El tiempo de ejecución menor se da con la variante sin optimización local. Esto es lógico debido a que no tiene que realizar los cálculos de optimización.
-
El tiempo de ejecución de la variante lamarckiana es inferior al de la variante balwidiana.
-
En general, los costes de las generaciones de la variante lamarckiana suele ir oscilando ascendentemente y descendientemente, mientras que la balwidiana suele permanecer decrecientemente y la variante sin optimización local siempre es decreciente.
-
Hay ejecuciones en las que la variante lamarckiana da mejor resultado que las demás, y a veces para otro tipo de tamaño y número de generaciones la variante balwidiana da mejor resultado. Casi nunca, la variante sin optimización local va a generar un mejor resultado que el resto.
-
La relación mejor coste obtenido entre el tiempo de ejecución es favorablemente hacia la variante lamarckiana, sin embargo, en los casos de que se requiera de una ejecución muy rápida y no se requiera tanta minimización en el coste, sería viable utilizar la versión sin optimización local.
Tras haber realizado este análisis previo, se han estado realizando pruebas para el problema propuesto en esta práctica.
A continuación se detalla la mejor solución obtenida y los parámetros utilizados en el algoritmo.
La mejor solución obtenida para el conjunto de datos “tai256c.dat” ha sido un coste de 46177746 respecto al mejor conocido actualmente que es 44759294.
Para obtener este resultado se han empleado los siguientes parámetros:
- Semilla utilizada: 2
- Operador de selección: Selección por torneo.
- Operador de cruce de individuos: Cruce en un punto
- Operador de mutación: Intercambio
- Número de generaciones: 100
- Número de individuos por población: 60
- Probabilidad de mutación: 0.01%.
- Probabilidad de selección: 0.6%
Adjunto a esta documentación se proporciona el conjunto de ficheros fuente con el que se ha elaborado esta aplicación. También se adjunta un archivo .pro por si se quiere importar directamente el proyecto en el IDE de desarrollo llamado “Qt creator”.
Una vez se ha compilado la aplicación, la forma de ejecutarla es la siguiente:
./<Nombre_ejecutable> <ruta_archivo_datos> <Número_generaciones> <número_semilla> <variante_algoritmo(lamarck|baldwin|fast)>
Para cualquier duda, estoy dispuesto a realizar una defensa o responder a cualquier cuestión relacionada con la práctica. Se puede poner en contacto conmigo a través de [email protected].
[1] Métodos Basados en Trayectorias y Entornos, página 7, disponible en https://sci2s.ugr.es/sites/default/files/files/Teaching/GraduatesCourses/Algoritmica/Tema02- BusquedaLocal- 12 - 13.pdf