POEM

Platform of Optimal Experiment Management (POEM)

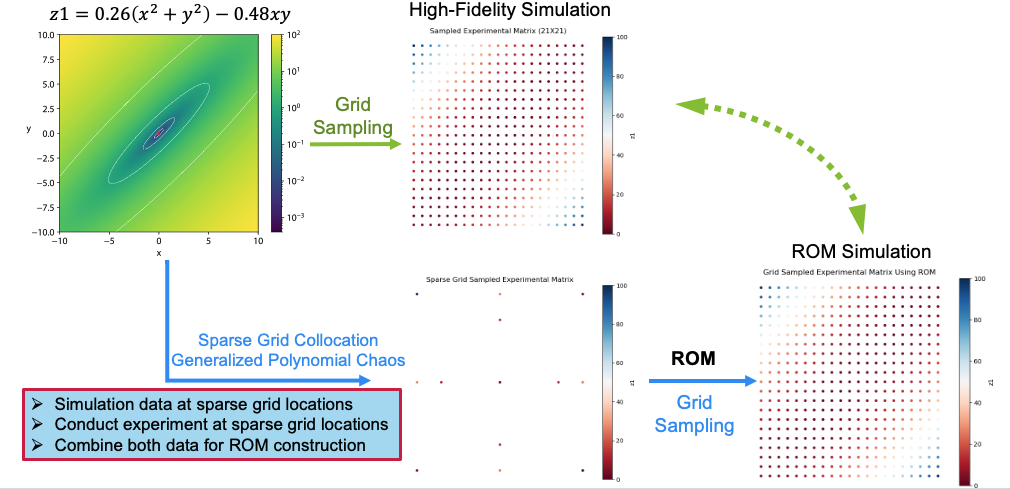
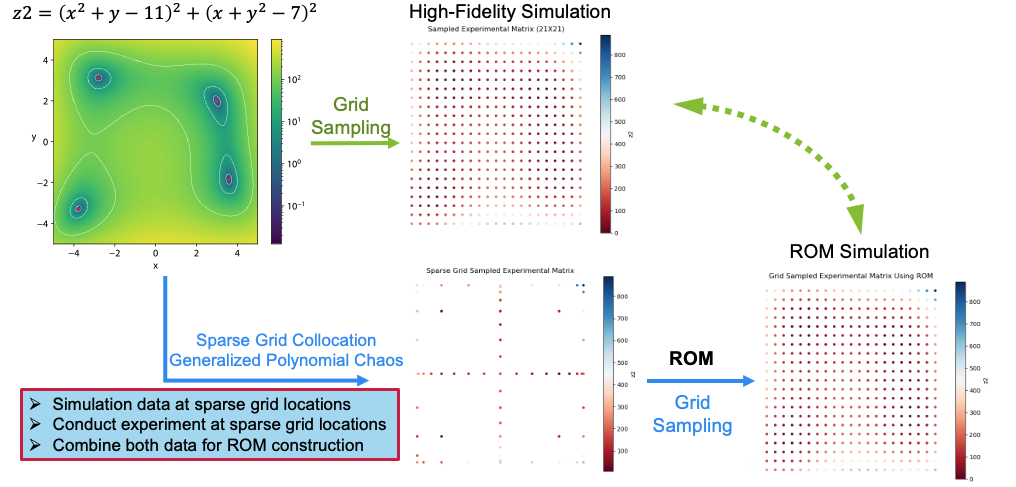
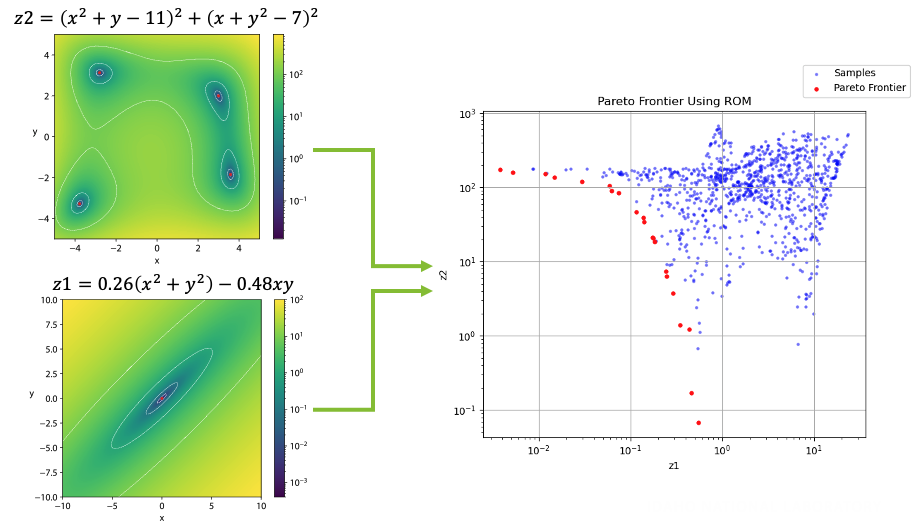
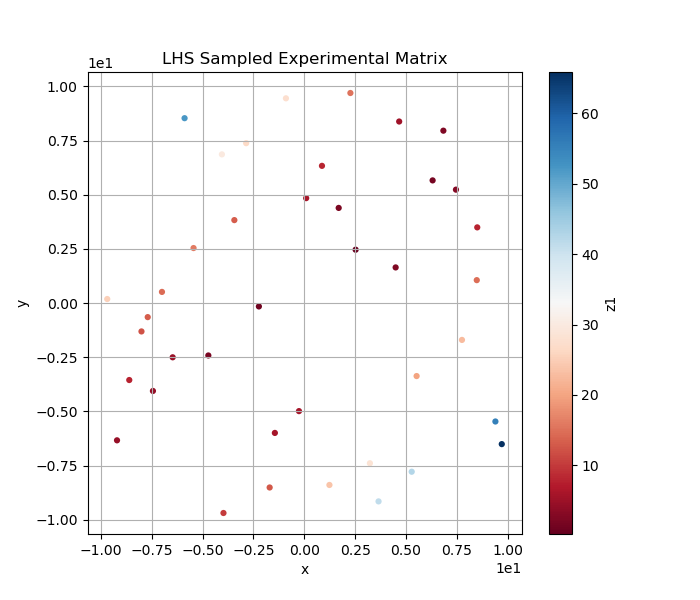
An optimal experimental design platform powered with automated machine learning to automatically guides the design of experiment to be evaluated. More information can be found at https://idaholab.github.io/POEM/

How to build html?

  pip install sphinx sphinx_rtd_theme nbsphinx sphinx-copybutton sphinx-autoapi
  conda install pandoc
  cd doc
  make html
  cd build/html
  python3 -m http.server

open your brower to: http://localhost:8000

Installation

conda create -n poem_libs python=3.10
conda activate poem_libs
pip install poem-ravenframework

Git Clone Repository

git clone [email protected]:idaholab/POEM.git

Test

cd POEM/tests
poem -i lhs_sampling.xml

or test without run

poem -i lhs_sampling.xml -nr

or

poem -i lhs_sampling.xml --norun

Capabilities

• Material thermal property modeling
• Design parameter optimization with multiple objectives
• Determining where to obtain new data in order to build accurate surrogate model
• Dynamic sensitivity and uncertainty analysis
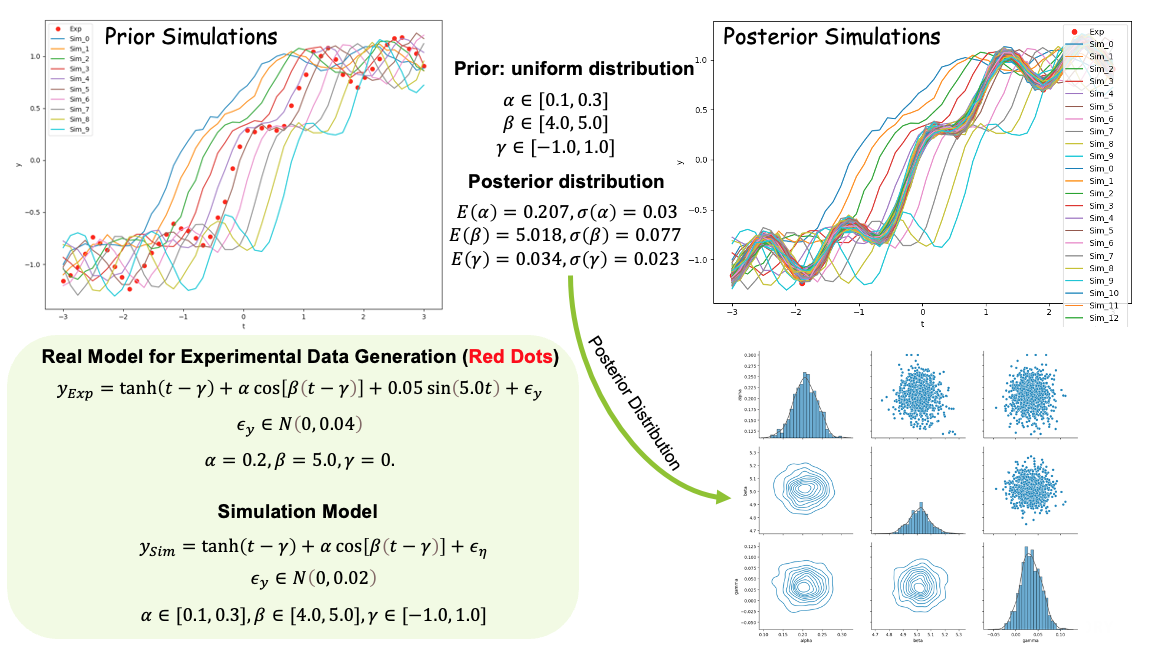
• Model calibration through Bayesian inference
• Data adjustment through generalized linear least square method
• Machine learning aided parameter space exploration
• Bayesian optimization for optimal experimental design
• Pareto Frontier to guide the design of experiment to be evaluated
• Sparse grid stochastic collocation to accelerate experimental design

Accelerate Experimental Design via Sparse Grid Stochastic Collocation Method

Matyas Function

Himmelblau's Function

Pareto Frontier

Accelerate Experimental Design via Bayesian Optimization Method

Matyas Function

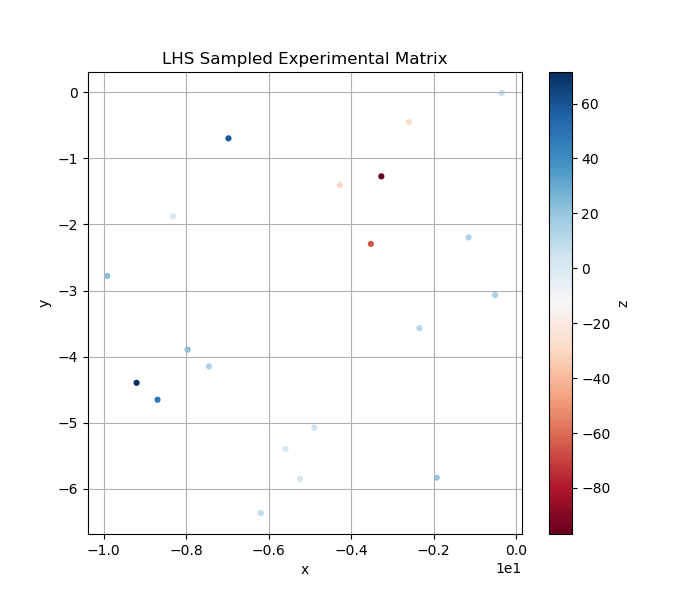
• LHS pre-samplings to simulate experiments
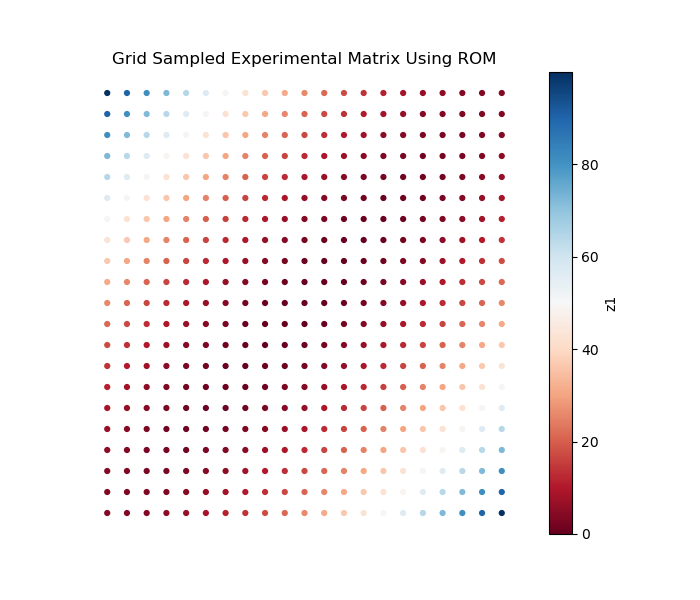
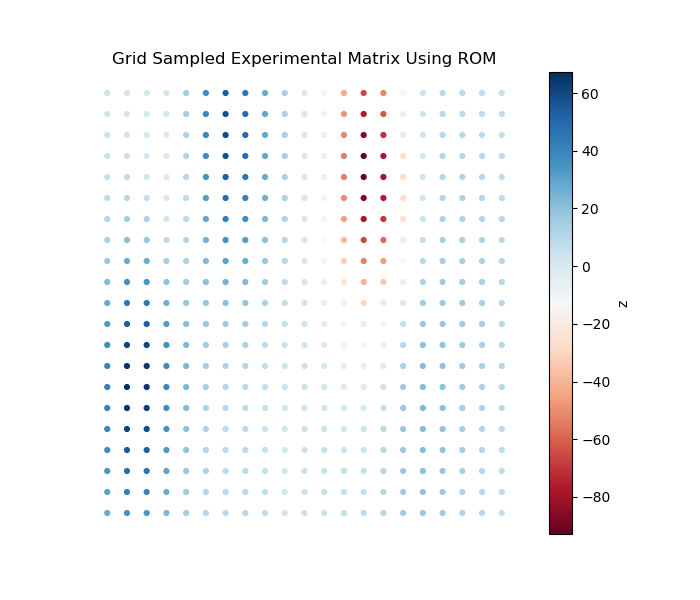
• Train Gaussian Process model with LHS samples, and use Grid approach to sample the trained Gaussian Process model
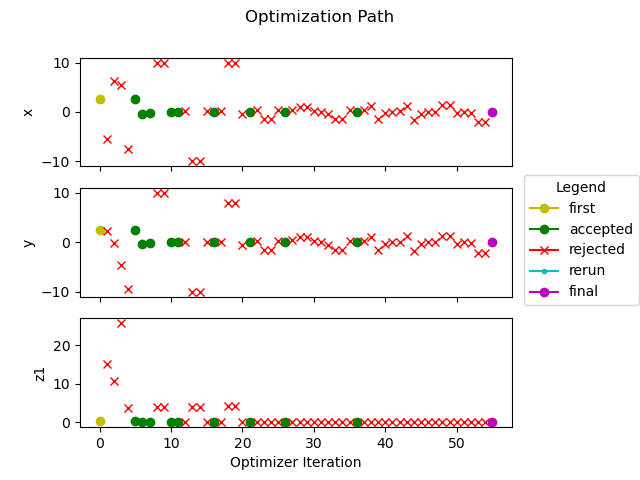
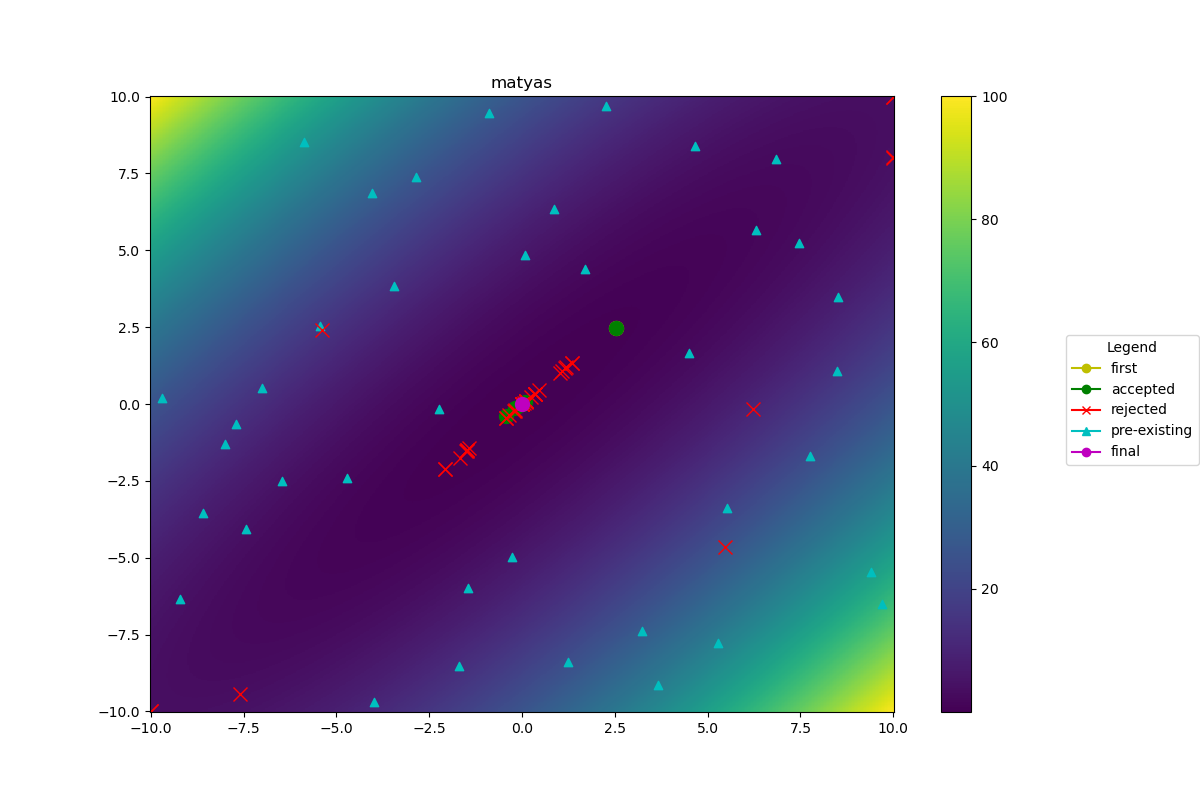
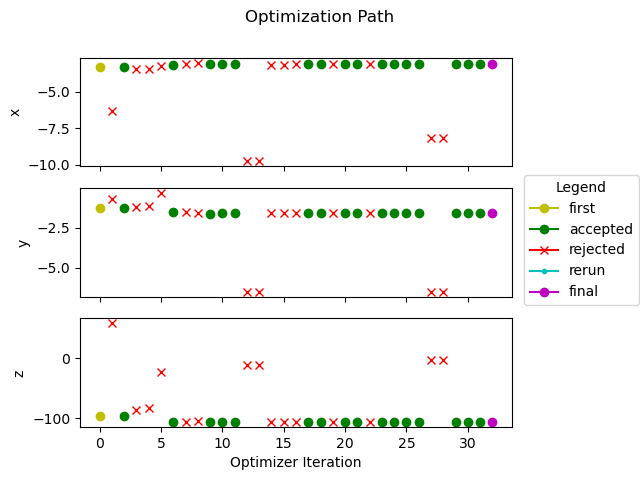
• Utilize Bayesian Optimization with pre-trained Gaussian Process model to optimize the experimental design

https://media.github.inl.gov/user/161/files/9021d2e6-b6b0-4c8f-96e0-3d0005f03cd4

Mishra

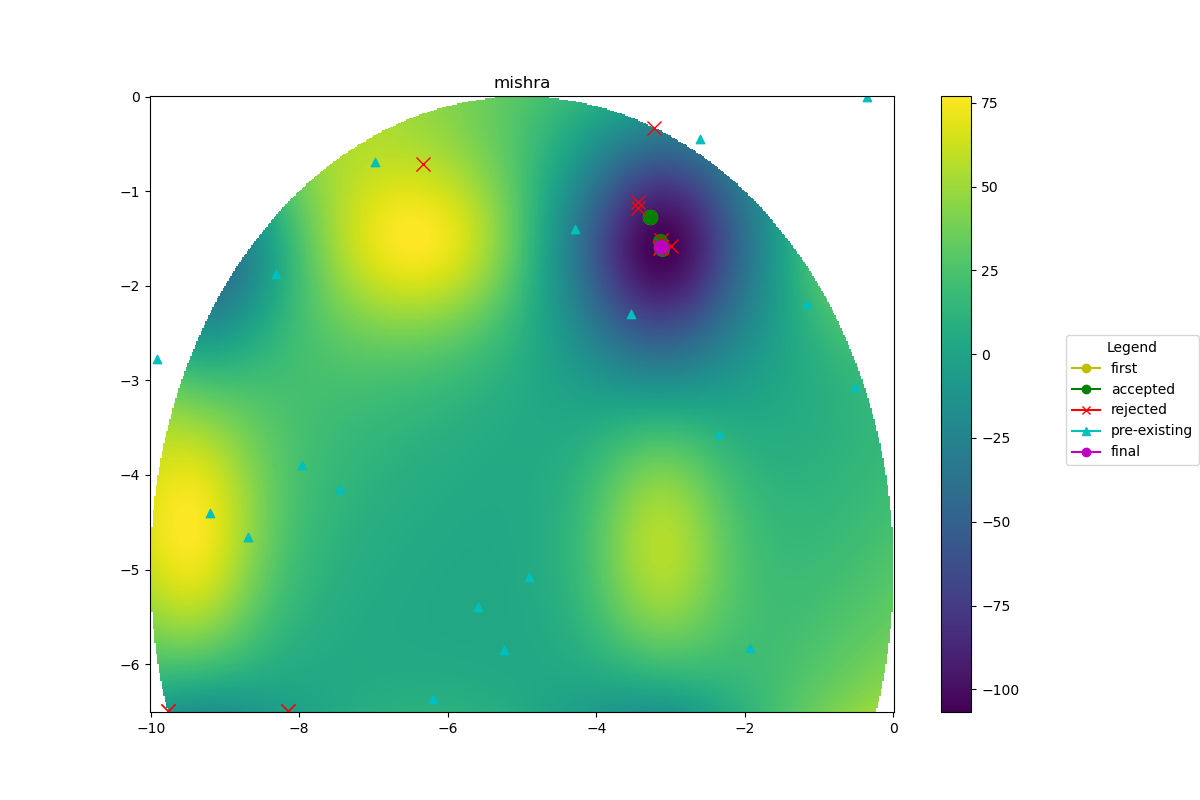
Bird Constrained Function

• LHS pre-samplings to simulate experiments
• Train Gaussian Process model with LHS samples, and use Grid approach to sample the trained Gaussian Process model
• Utilize Bayesian Optimization with pre-trained Gaussian Process model to optimize the experimental design

https://media.github.inl.gov/user/161/files/86dc8928-7017-4a4b-893c-f77286ded0d4

Dynamic Sensitivity Analysis

• Regression based method
• Sobol index based method

Bayesian Model Calibration

Analytic High-Dimensional Problem

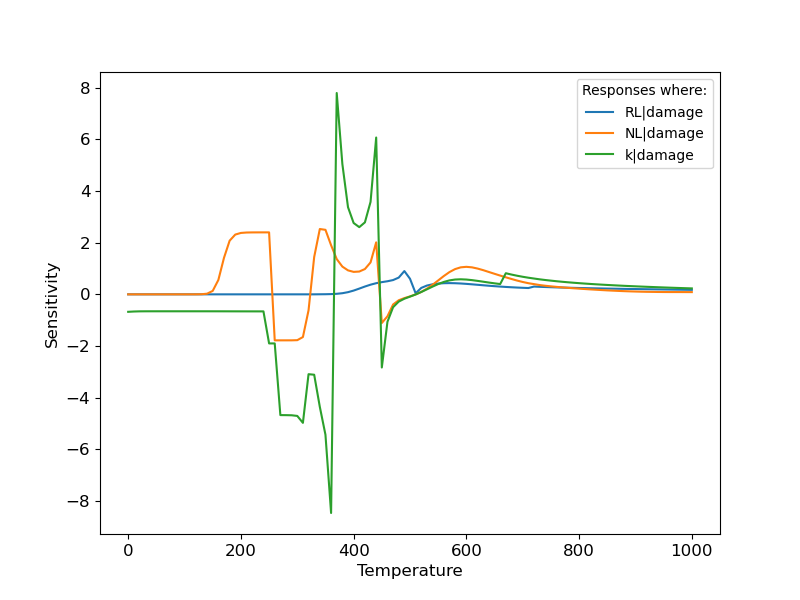
A python analytic problem with 50 responses, three input parameters with uniform prior distributions.