Introduction to Time Series Analysis

Time Series

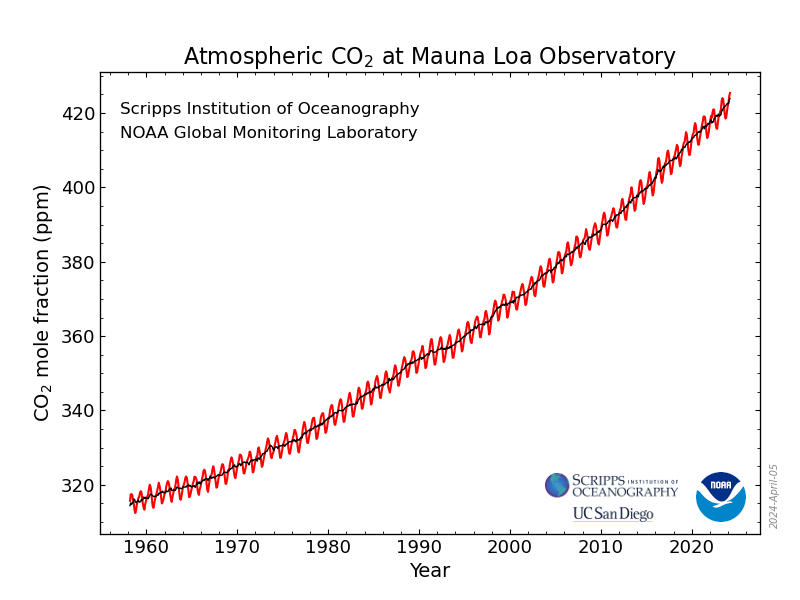
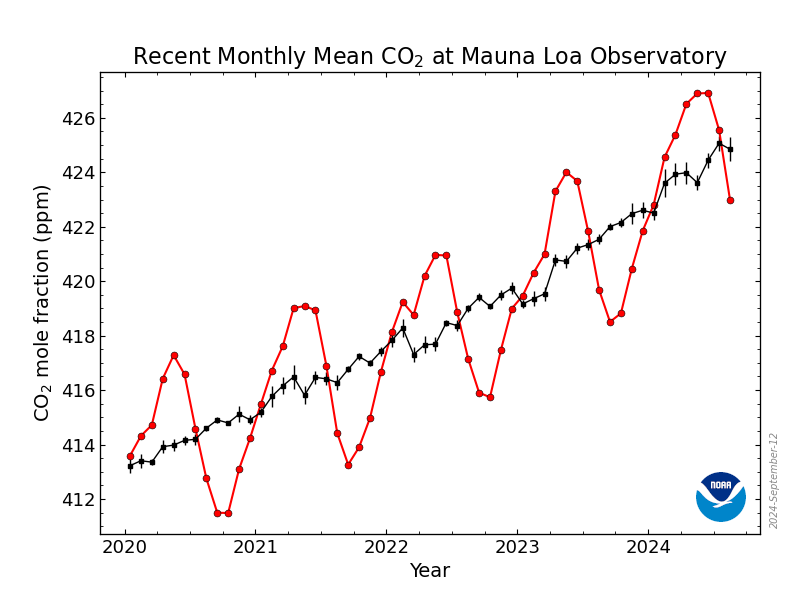
In mathematics, a time series is a series of data points indexed in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average.

A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements.

Time series analysis comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series forecasting is the use of a model to predict future values based on previously observed values.

Time series analysis and forecasting is a branch of statistics that deals with analyzing and predicting the patterns and trends in time series data.

Some of the main topics in time series analysis and forecasting include:

Time series data: This topic covers the different types of time series data and how to collect, organize, and visualize them.
Time domain analysis: This topic covers the basic time domain techniques such as trend analysis, seasonality, and cyclical patterns.
Frequency domain analysis: This topic covers the Fourier analysis and other frequency domain techniques to explore and extract the hidden periodicities in time series data.
Stationarity and non-stationarity: This topic covers the concepts of stationarity, non-stationarity, and how to test and transform time series data to meet the stationarity assumption.
Autocorrelation and cross-correlation: This topic covers the concepts of autocorrelation and cross-correlation functions and how to use them to detect and measure the relationship between lagged values of a time series.
Time series models: This topic covers the different types of time series models such as ARIMA, SARIMA, and exponential smoothing models and how to estimate and diagnose them.
Forecasting: This topic covers the various methods and techniques used for forecasting future values of a time series, such as ARIMA, exponential smoothing, and neural network models.
Model selection and validation: This topic covers the methods and techniques for selecting the best time series model for a particular data set and how to validate the performance of the selected model.
Multivariate time series analysis: This topic covers the analysis of time series data that involve multiple variables, such as VAR and VECM models.

Overall, time series analysis and forecasting is a vast and important area of study that has many practical applications in fields such as economics, finance, engineering, and environmental sciences.

Components of a Time Series

Before we begin describing time series, we describe a list of basic concepts:

Trend: It refers to whether data values increase or decrease with time.

Seasonality and cycles: Seasonality is a repeated behavior of data that occurs on the regular interval of time. It means that there are patterns that repeat themselves after some interval of the period then we call it seasonality.

The difference between seasonality and cycles is that seasonality is always has a fixed and a known frequency. The cycles also have rise and fall peaks but not a fixed frequency. The Solar cycle duration is nearly 11 years.

Variations and Irregularities. The variation and irregular patterns are not fixed frequency patterns and they are or short duration and non-repeating.
Stationary and Non-Stationary. A stationary process has the property that the mean, variance and autocorrelation structure do not change over time.

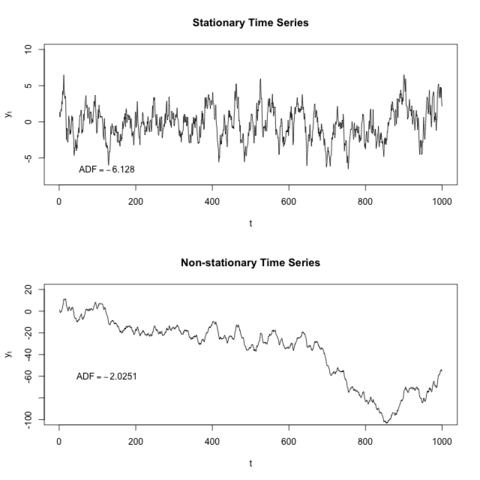
If the series is not stationary then we make the data to be stationary with some method or test.

Rolling Statistics and Dickey-Fuller Test.

These two tests are performed to check the stationarity of the time series.

The Rolling statistics is that we check of moving average and moving variance of the series that it varies with time or not. It is a kind of visual type test result.

The Dickey-Fuller test is a type of hypothesis test in which the test statistic value is smaller than the p-value then we will reject the null hypothesis. The null hypothesis in this is time series is non-stationary.

Time series Forecasting

Moving Averages

In statistics, a moving average (rolling average or running average) is a calculation to analyze data points by creating a series of averages of different subsets of the full data set. It is also called a moving mean (MM)[1] or rolling mean and is a type of finite impulse response filter. Variations include: simple, cumulative, or weighted and the exponential moving average forms.

The Moving Average Model

The moving average model in time series analysis smoothens the time series curve by computing the average of all the data points in a fixed-width sliding window and replacing those points with the computed value. The sliding window size (w) is fixed, and the window moves with a specified stride over the data, creating a new series from the average values.

Together with the autoregressive (AR) model, the moving-average model is a special case and key component of the more general ARMA and ARIMA models of time series,[3] which have a more complicated stochastic structure. Contrary to the AR model, the finite MA model is always stationary.

The moving-average model should not be confused with the moving average, a distinct concept despite some similarities.

Please see the corresponding Jupyter Notebook Example for Time Series Analysis.