This is the first draft of an Incremental (Fully Dynamic) Constrained_Delaunay_Triangulation written from scratch in the Nim programming language.
The implementation is based on the Kallmann paper
and some other papers cited in the source code.
As underlying data structure the Quad-Edge structure is used. For point location we use the "jump and walk" algorithm, which is very simple and generally fast enough.
This type of CDT allows insertion and removal of points and line segments in arbitrary order. Intersecting and overlapping segments as well as duplicated points are supported. Typical running time for triangulations with N vertices is O(N ^ (1/3)) for single insert or delete operations, which is not too far away from the optimal (log N) case.
As this is the first draft, much more testing is necessary. (Well known problems for CDTs can be numerically instabilities.) The API will change when we start using this library, it may become more generic, and more traversal operations will be added.
Maybe most serious limitation is, that we have to specify an initial bounding box for all of our data points when we create the CDT. This is a common practice and simplifies the algorithm. Maybe later we can remove this restriction.
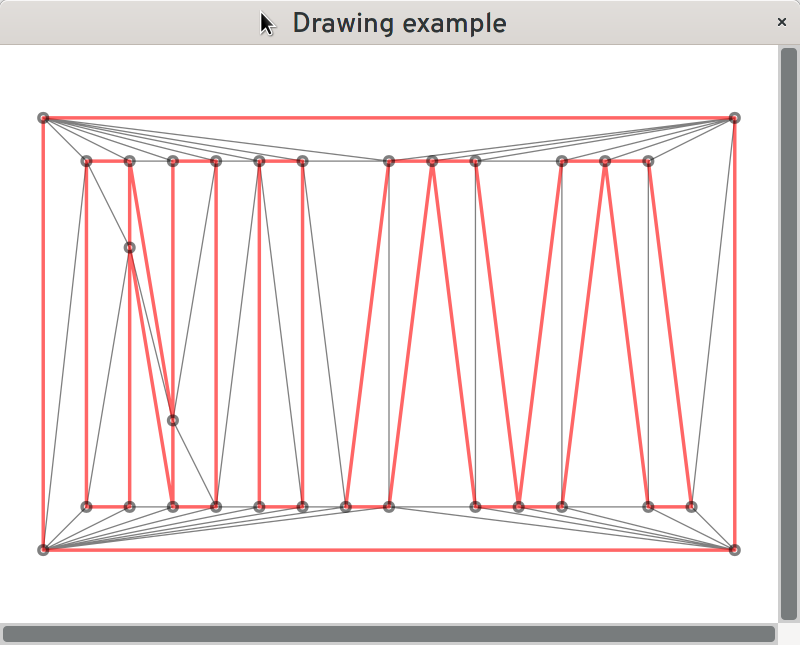
For testing currently the files test0.nim and test.nim are provided. Test0.nim is a very basic test with only textual output. Test.nim generates graphical output as shown above, but you need GTK3 and gintro Nim bindings for it.
Sketch of basic use is like this:
import cdt/[dt, vectors, edges, types]
proc main =
var dt: DelaunayTriangulation = initDelaunayTriangulation(initVector(minX, minY), initVector(maxX, maxY))
discard dt.insert(Vector(x: 5, y: 10)) # insert a single point
let cid dt.insert(Vector(x: 20, y: 30), Vector(x: 30, y: 90)) # insert a constrained line segment
discard dt.removeConstraint(cid) # remove an segment
main()|
Note
|
Related work: https://github.com/Nycto/DelaunayNim |