This was my university assignment provided by Dr. Andrew Godbout. I thank him for his mentorship. I also thank my help center tutor Mr. Will Taylor for his guidance.

To explain my assignment in short, fireflies synchronise their light flashing with the neighboring fireflies. This program simulates this synchronisation.

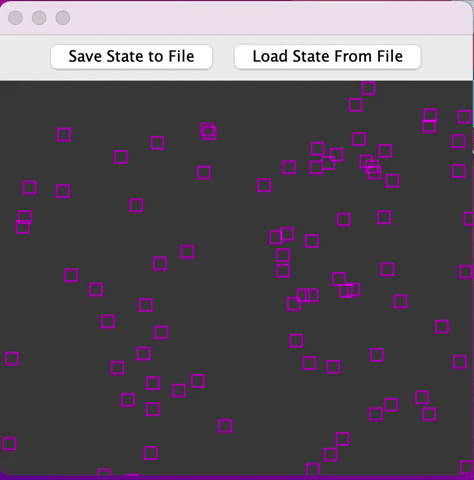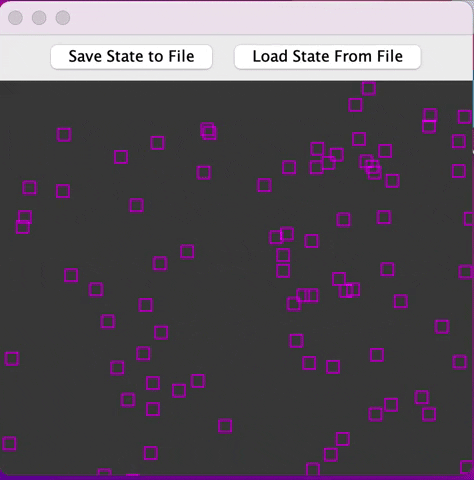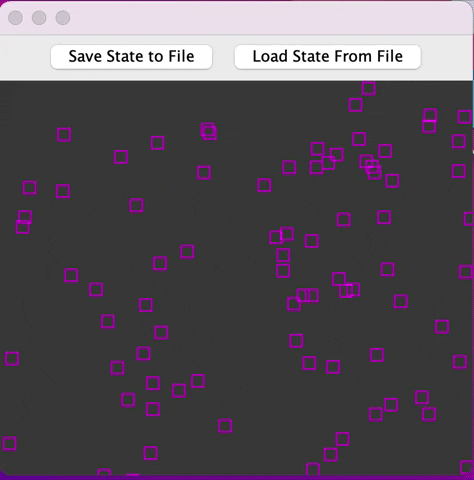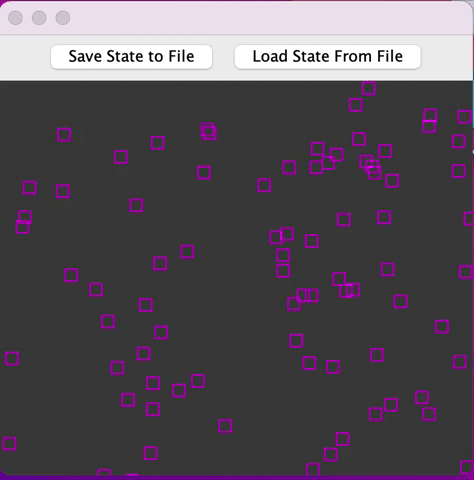
We Save state to File using the Java Serializable interface and rerun the project again to Load the state from file as follows:

Please clone the project and run the Firefly2Viewer class in your IDE to see the program in action.

Please read the section below Assignment 4 to understand the math behind the firefly synchronisation based on coupled oscillators.

Assignment 4

In the wild, fireflies display a natural tendency to synchronize their flashing.

They will even synchronize their flashing with a pretend firefly. For example: https://www.youtube.com/watch?v=ZGvtnE1Wy6U

Synchronization can be modeled mathematically and simulated using some reasonably simply mathematics borrowed from how coupled oscillators work. Coupled oscillators are two or more repeating things that transfer energy between themselves (often this results in them becoming synchronized). Steven Strogatz has some great talks about synchronization and coupled oscillators in case you want a bit more information: https://www.ted.com/talks/steven_strogatz_on_sync?language=en

In this assignment you will model, simulate and animate the interactions of a collection of fireflies (see for example: https://youtu.be/xWY7FOas2FU) .

To model a Firefly you should know that for our purposes, a firefly has:

1. A current phase (φ)- this is a number between 0 and 2π. It represents how close a fly is to flashing their light. A fly flashes its light when φ reaches 2π. After flashing their light the phase of the firefly resets to 0. When we first create a firefly they will start out at a random phase value (i.e., you pick a random number in the interval 0 to 2π).

2. A natural flashing frequency (ω) this is the rate of change of the phase of the firefly. For every firefly this should be 0.785, i.e., a firefly will flash its light roughly every 8 time steps: 0.785 * 8 is approximately 2π

3. A current flashing frequency (δφ/δt) - this is the current rate at which the firefly is flashing its light. This is ω except when a firefly is startled in which case the flashing frequency will deviate from ω. At a time step (t+1) the following formula updates the phase of the fly: φ(t+1) = φ(t) + δφ/δt

4. The ability to broadcast a flash, boolean. In other words a simple boolean value that is false if the firefly is not flashing and true when the firefly does flash.

5. A startled factor, K. This how startled a firefly becomes when it sees another firefly that is near to it flashing its light. When a firefly becomes startled it either speeds up or slows down its flashing frequency temporarily in response to what it has seen. K is always 0.1 and never changes.

6. A location on the screen, (x,y). This is the location where the firefly it. (x,y) is randomly chosen when the firefly is created. It is the pixel location for that fly.

7. An eyesight range, M=100 pixels. This is the radius of a circle centred at the fly's position (x,y) where the fly can see any other fly within that circle. A firefly may possibly be startled by any fly that is within M units away from (x,y). Any flies farther away than M will not impact a given fly. Recall distance, d is calculated as d=

A Firefly will flash at its normal frequency ω except for the following:

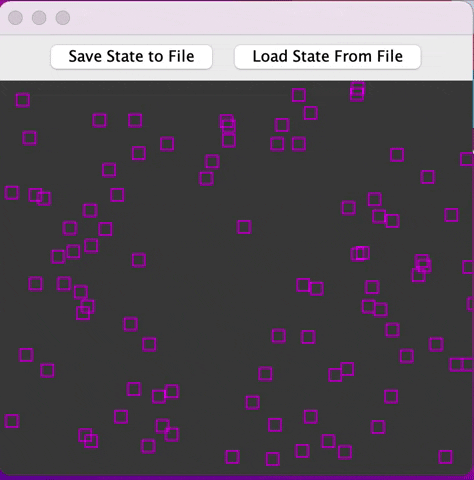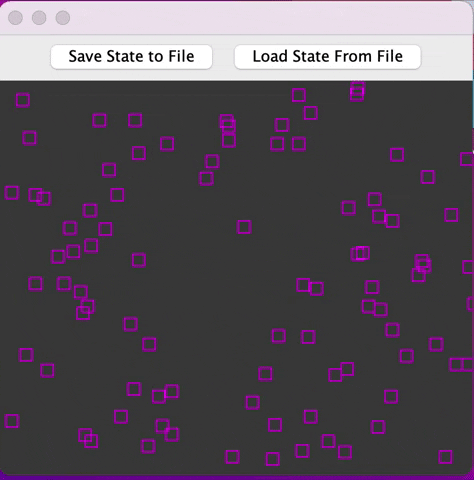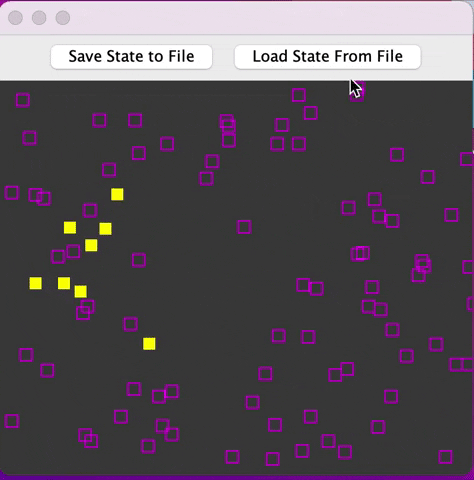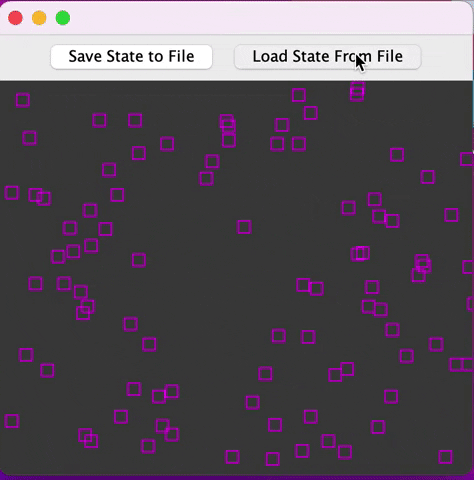
Any time it sees another fly flash its light (that is any firefly that is within a radius of M away), the fly becomes startled and changes its flashing frequency temporarily according to the below rule of coupled oscillators, where N is the number of other flies it sees flashing:

δφ/δt = ω + K * N * Sin( 2π - φ))

obviously when N is 0 (it sees no flies flashing) this degrades back to δφ/δt = ω

The fly will stay in this started state for 1 time step (thus the current frequency is recalculated as above each time step).

Your program should draw every fly at each time step. Use a single thread to update all of the fireflies. Much like our animation example from class you should ensure that your animation may not be drawn until after a time step has been fully simulated, i.e., use a reentrant lock to ensure the flies are fully updated before anyone else can access them. A firefly may be shown on the screen as a square centred at the given location (or something more creative if you like).

Hint: Get your solution working with 1 fly first. Use some print screens and make sure phase is advancing correctly and the fly is flashing properly. Then move to 2 flies and then to 100.

Deliverables:

Create an animation displaying your fireflies which may look something like this: https://youtu.be/xWY7FOas2FU .

You should update all of your fireflies on a single thread. You may use simple java graphics to draw the fireflies - g.drawRect or g.fillRect for example.

Initialization

Create 100 Fires Flies with random position as specified above. All within a Frame of 400 pixels x 400 pixels.

Animation

For an infinite number of iterations the following takes place:

1. φ of each fly is advanced by 1 time step. i.e., φ = φ + φ/δt

2. φ of each fly is displayed simply as an empty box of size 10 pixels x 10 pixels if φ did not pass 2π during the last time step and a filled box of the same size otherwise.

Bonus Points

For 2 bonus points:

Add a button to the screen which saves the current state of your simulation (all of the fireflies including all information required to reproduce the flies out to a binary file. Further add a button to restore to the previously saved state and continue the animation from that saved state. See youtube video linked above for an example which may help to clarify.

Gradables:

Gradable	Points	Notes
Readability	2 Points	Proper names, method lengths, indentation, etc
Design	3 Points	Use of classes, methods and variables
Functionality	5 Points	Does the simulation run correctly