nanoflann is a C++11 header-only library for building KD-Trees of datasets with different topologies: R2, R3 (point clouds), SO(2) and SO(3) (2D and 3D rotation groups). No support for approximate NN is provided. nanoflann does not require compiling or installing. You just need to #include <nanoflann.hpp> in your code.
This library is a fork of the flann library (git) by Marius Muja and David G. Lowe, and born as a child project of MRPT. Following the original license terms, nanoflann is distributed under the BSD license. Please, for bugs use the issues button or fork and open a pull request.
Cite as:
@misc{blanco2014nanoflann,
title = {nanoflann: a {C}++ header-only fork of {FLANN}, a library for Nearest Neighbor ({NN}) with KD-trees},
author = {Blanco, Jose Luis and Rai, Pranjal Kumar},
howpublished = {\url{https://github.com/jlblancoc/nanoflann}},
year = {2014}
}
- Easiest way: clone this GIT repository and take the
include/nanoflann.hppfile for use where you need it. - macOS users can install
nanoflannwith Homebrew with:or$ brew install brewsci/science/nanoflann
$ brew tap brewsci/science $ brew install nanoflann
- Linux users can install it with Linuxbrew with:
brew install homebrew/science/nanoflann - List of stable releases. Check out the CHANGELOG
Although nanoflann itself doesn't have to be compiled, you can build some examples and tests with:
sudo apt-get install build-essential cmake libgtest-dev libeigen3-dev
mkdir build && cd build && cmake ..
make && make test
-
Browse the Doxygen documentation.
-
Important note: If L2 norms are used, notice that search radius and all passed and returned distances are actually squared distances.
- KD-tree look-up with
kdd_search()andradius_search(): pointcloud_kdd_radius.cpp - KD-tree look-up on a point cloud dataset: pointcloud_example.cpp
- KD-tree look-up on a dynamic point cloud dataset: dynamic_pointcloud_example.cpp
- KD-tree look-up on a rotation group (SO2): SO2_example.cpp
- KD-tree look-up on a rotation group (SO3): SO3_example.cpp
- KD-tree look-up on a point cloud dataset with an external adaptor class: pointcloud_adaptor_example.cpp
- KD-tree look-up directly on an
Eigen::Matrix<>: matrix_example.cpp - KD-tree look-up directly on
std::vector<std::vector<T> >orstd::vector<Eigen::VectorXd>: vector_of_vectors_example.cpp - Example with a
Makefilefor usage throughpkg-config(for example, after doing a "make install" or after installing from Ubuntu repositories): example_with_pkgconfig/ - Example of how to build an index and save it to disk for later usage: saveload_example.cpp
-
Execution time efficiency:
- The power of the original
flannlibrary comes from the possibility of choosing between different ANN algorithms. The cost of this flexibility is the declaration of pure virtual methods which (in some circumstances) impose run-time penalties. Innanoflannall those virtual methods have been replaced by a combination of the Curiously Recurring Template Pattern (CRTP) and inlined methods, which are much faster. - For
radiusSearch(), there is no need to make a call to determine the number of points within the radius and then call it again to get the data. By using STL containers for the output data, containers are automatically resized. - Users can (optionally) set the problem dimensionality at compile-time via a template argument, thus allowing the compiler to fully unroll loops.
nanoflannallows users to provide a precomputed bounding box of the data, if available, to avoid recomputation.- Indices of data points have been converted from
inttosize_t, which removes a limit when handling very large data sets.
- The power of the original
-
Memory efficiency: Instead of making a copy of the entire dataset into a custom
flann-like matrix before building a KD-tree index,nanoflannallows direct access to your data via an adaptor interface which must be implemented in your class.
Refer to the examples below or to the C++ API of nanoflann::KDTreeSingleIndexAdaptor<> for more info.
- Building KD-trees with a single index (no randomized KD-trees, no approximate searches).
- Fast, thread-safe querying for closest neighbors on KD-trees. The entry points are:
- nanoflann::KDTreeSingleIndexAdaptor<>
::knnSearch()- Finds the
num_closestnearest neighbors toquery_point[0:dim-1]. Their indices are stored inside the result object. See an example usage code.
- Finds the
- nanoflann::KDTreeSingleIndexAdaptor<>
::radiusSearch()- Finds all the neighbors to
query_point[0:dim-1]within a maximum radius. The output is given as a vector of pairs, of which the first element is a point index and the second the corresponding distance. See an example usage code.
- Finds all the neighbors to
- nanoflann::KDTreeSingleIndexAdaptor<>
::radiusSearchCustomCallback()- Can be used to receive a callback for each point found in range. This may be more efficient in some situations instead of building a huge vector of pairs with the results.
- nanoflann::KDTreeSingleIndexAdaptor<>
- Working with 2D and 3D point clouds or N-dimensional data sets.
- Working directly with
Eigen::Matrix<>classes (matrices and vectors-of-vectors). - Working with dynamic point clouds without a need to rebuild entire kd-tree index.
- Working with the distance metrics:
R^N: Euclidean spaces:L1(Manhattan)L2(squared Euclidean norm, favoring SSE2 optimization).L2_Simple(squared Euclidean norm, for low-dimensionality data sets like point clouds).
SO(2): 2D rotational groupmetric_SO2: Absolute angular diference.
SO(3): 3D rotational group (better suppport to be provided in future releases)metric_SO3: Inner product between quaternions.
- Saves and load the built indices to disk.
- GUI based support for benchmarking multiple kd-tree libraries namely nanoflann, flann, fastann and libkdtree.
- Use other distance metrics apart from L1, L2, SO2 and SO3.
- Support for SE(3) groups.
- Only the C++ interface exists: there is no support for C, MATLAB or Python.
- There is no automatic algorithm configuration (as described in the original Muja & Lowe's paper).
You can directly drop the nanoflann.hpp file in your project. Alternatively,
the CMake standard method is also available:
- Build and "install" nanoflann. Set
CMAKE_INSTALL_PREFIXto a proper path and then executemake install(Linux, OSX) or build theINSTALLtarget (Visual Studio). - Then, add something like this to the CMake script of your project:
# Find nanoflannConfig.cmake:
find_package(nanoflann)
add_executable(my_project test.cpp)
# Make sure the include path is used:
target_link_libraries(my_project nanoflann::nanoflann)
A KD-tree is... well, a tree :-). And as such it has a root node, a set of intermediary nodes and finally, "leaf" nodes which are those without children.
Points (or, properly, point indices) are only stored in leaf nodes. Each leaf contains a list of which points fall within its range.
While building the tree, nodes are recursively divided until the number of points inside is equal or below some threshold. That is leaf_max_size. While doing queries, the "tree algorithm" ends by selecting leaf nodes, then performing linear search (one-by-one) for the closest point to the query within all those in the leaf.
So, leaf_max_size must be set as a tradeoff:
- Large values mean that the tree will be built faster (since the tree will be smaller), but each query will be slower (since the linear search in the leaf is to be done over more points).
- Small values will build the tree much slower (there will be many tree nodes), but queries will be faster... up to some point, since the "tree-part" of the search (logarithmic complexity) still has a significant cost.
What number to select really depends on the application and even on the size of the processor cache memory, so ideally you should do some benchmarking for maximizing efficiency.
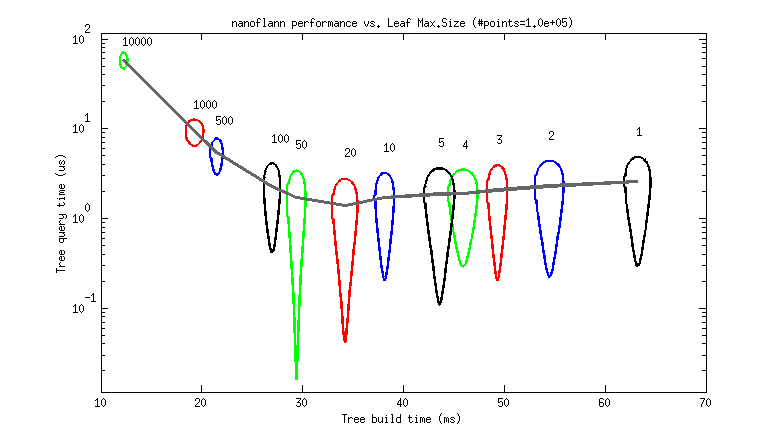
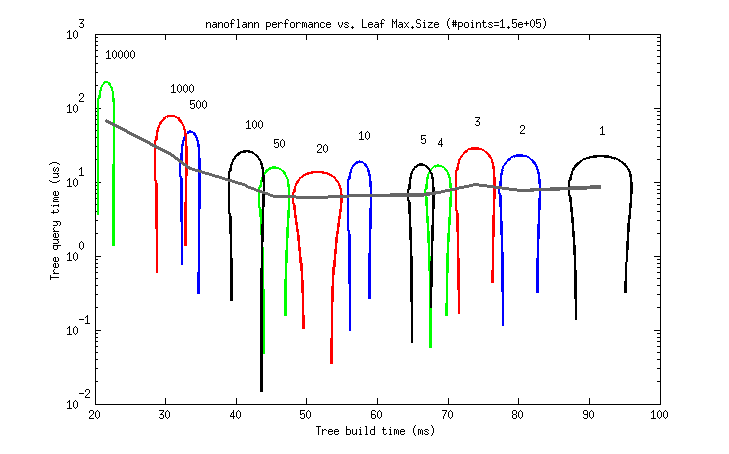
But to help choosing a good value as a rule of thumb, I provide the following two benchmarks. Each graph represents the tree build (horizontal) and query (vertical) times for different leaf_max_size values between 1 and 10K (as 95% uncertainty ellipses, deformed due to the logarithmic scale).
- A 100K point cloud, uniformly distributed (each point has (x,y,z)
floatcoordinates):
- A ~150K point cloud from a real dataset (
scan_071_points.datfrom the Freiburg Campus 360 dataset, each point has (x,y,z)floatcoordinates):
So, it seems that a leaf_max_size between 10 and 50 would be optimum in applications where the cost of queries dominates (e.g. ICP). At present, its default value is 10.
This parameter is really ignored in nanoflann, but was kept for backward compatibility with the original FLANN interface. Just ignore it.
Refer to the "Why a fork?" section above for the main optimization ideas behind nanoflann.
Notice that there are no explicit SSE2/SSE3 optimizations in nanoflann, but the intensive usage of inline and templates in practice turns into automatically SSE-optimized code generated by the compiler.
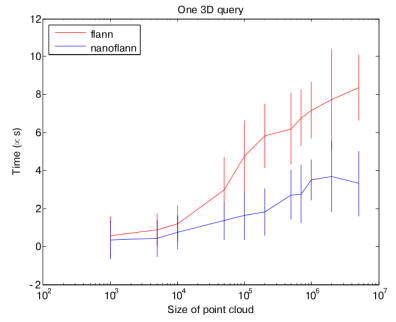
The most time-consuming part of many point cloud algorithms (like ICP) is querying a KD-Tree for nearest neighbors. This operation is therefore the most time critical.
nanoflann provides a ~50% time saving with respect to the original flann implementation (times in this chart are in microseconds for each query):
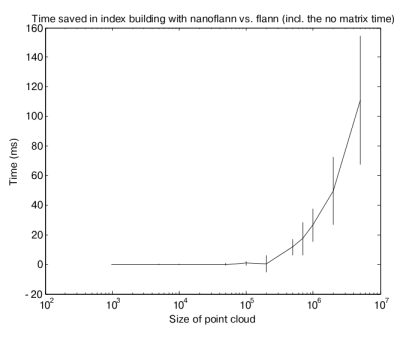
Although most of the gain comes from the queries (due to the large number of them in any typical operation with point clouds), there is also some time saved while building the KD-tree index, due to the templatized-code but also for the avoidance of duplicating the data in an auxiliary matrix (times in the next chart are in milliseconds):
These performance tests are only representative of our testing. If you want to repeat them, read the instructions in perf-tests
- FLANN - Marius Muja and David G. Lowe (University of British Columbia).
- FASTANN - James Philbin (VGG, University of Oxford).
- ANN - David M. Mount and Sunil Arya (University of Maryland).
- libkdtree++ - Martin F. Krafft & others.
Note: The project logo is due to CedarSeed