Hedging options by using Monte Carlo simulations or real data
After inputting the parameters (e.g. r, sig(vol), dt), this project can give users the results of dynamic delta hedging. The dynamic stock price can come from Monte Carlo Simulation or real data.
Python 3.X should be installed on your machine.
- Import different files to run the code:
<import delta_hedging_mc>- Daily delta hedging when market close
- stock price: Monte Carlo Simulation
<import hedging_based_s>- Delta hedging based on changes in stock price
- stock price: Monte Carlo Simulation
<import hedging_real_data>- Delta hedging based on changes in stock price
- stock price: real price
- The parameters:
k = strike price
s0 = initial stock price
dt = t/T = time to maturity
rf = remaining time
r = risk-less short rate
sig = volatility of stock value
m = the number of path nodes
n = the number of simulations
name: "c"=call, "p"=put
towards: buy=1, sell=-1
number = the number of contract
<import delta_hedging_mc>
Suppose we buy 100 numbers of call option. The parameters are as follows:
strike price = 100; initial stock price = 100; time to maturity = 20/250 = 0.08;
risk-less short rate = 0.03; volatility of stock value = 0.2
the number of path nodes = 20; the number of simulations = 100000
Then one price path can be simulated based on Monte Carlo method:
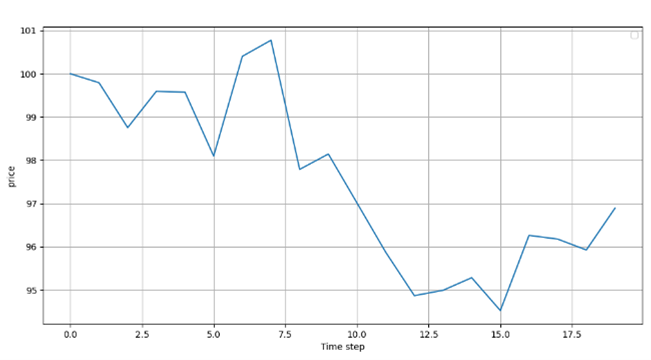
Following this price path, the result about daily delta hedging when market close are as follows:
s k value delta underlying_position PoL_in_stock
0 100.000000 100 2.249024 0.528186 -53.0 0.000000
1 99.792657 100 2.088297 0.512475 -51.0 10.989176
2 98.754161 100 1.557154 0.433872 -43.0 52.963311
3 99.594844 100 1.874472 0.494953 -49.0 -36.149385
4 99.574226 100 1.803350 0.491589 -49.0 1.010282
5 98.096180 100 1.127525 0.370275 -37.0 72.424269
6 100.403404 100 2.095604 0.557338 -56.0 -85.367279
7 100.775555 100 2.235728 0.589557 -59.0 -20.840460
8 97.788877 100 0.841258 0.324372 -32.0 176.213957
9 98.144736 100 0.890919 0.346811 -35.0 -11.387459
10 97.011756 100 0.508059 0.239333 -24.0 39.654271
11 95.874580 100 0.249233 0.143943 -14.0 27.292239
12 94.869292 100 0.108490 0.076725 -8.0 14.074034
13 94.992759 100 0.088016 0.067702 -7.0 -0.987740
14 95.283589 100 0.077165 0.064186 -6.0 -2.035809
15 94.524201 100 0.023866 0.025253 -3.0 4.556329
16 96.263196 100 0.071753 0.070270 -7.0 -5.216984
17 96.177148 100 0.032285 0.039910 -4.0 0.602333
18 95.925056 100 0.005943 0.010631 -1.0 1.008369
19 96.892785 100 0.002529 0.006576 -1.0 -0.967729
Repeating this process 100000 times and then calcultaing profit each time, we can get returns best fit distribution. It is a normal distribution centered on 0.
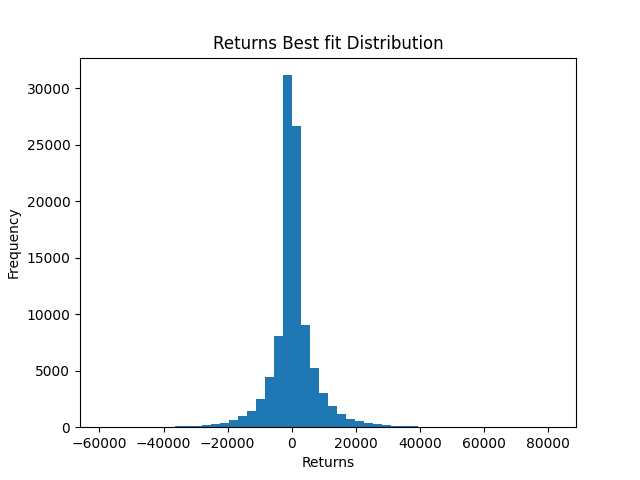
<import hedging_real_data>
Delta will be hedged when the the variation of the stock price is greater or less than sigma / 16
First, we select the closing price of HC2110 in every 30 minutes from July 2, 2021 to July 29, 2021 HC2110.xls
The following are parameters:
Suppose expiration time is on July 29, 2021.
r = risk-less short rate = 0.03
sig = volatility of stock value = 0.21
Suppose we bought 100 numbers of call option
The results are as follows:
s s (prior) k ds value delta underlying_position position (prior) time PoL
0 5402.0 0.0 5402 0.000000 151.749074 0.533275 -53.0 0.0 2021-7-2 09:30:00 0.0
1 5580.0 5402.0 5402 0.015653 249.045541 0.716173 -72.0 -53.0 2021-7-6 09:30:00 -9434.0
2 5883.0 5580.0 5402 0.015186 489.418648 0.940885 -94.0 -72.0 2021-7-12 09:30:00 -21816.0
3 5955.0 5883.0 5402 0.014999 556.160107 0.969373 -97.0 -94.0 2021-7-14 09:30:00 -6768.0
4 5895.0 5955.0 5402 -0.015531 496.853432 0.963866 -96.0 -97.0 2021-7-16 13:45:00 5820.0
5 5909.0 5895.0 5402 0.013377 507.197840 0.991441 -99.0 -96.0 2021-7-22 14:15:00 -1344.0
6 5974.0 5909.0 5402 -0.014517 571.704391 0.999868 -100.0 -99.0 2021-7-26 13:45:00 -6435.0
--------------------------------------------------------------------------------------------------------------------------------------
profit in options market is 41995
profit in stock market is -39977
the final profit is 2018
@ITNeri