-
Notifications
You must be signed in to change notification settings - Fork 22
A. Introduction
The breakthroughs in different areas achieved by the use of deep learning models come along with associated high energy costs. The increasing computational demands of these models, along with the projected traditional hardware limitations, are shifting the paradigm towards innovative hardware solutions, where analogue-based components for application-specific integrated circuits are keenly being sought. Dopant-network processing units (DNPUs) are a novel concept consisting of a lightly doped semiconductor surface, edged with several electrodes, where hopping conductance between atomic-scale dopant networks is the dominant charge transport mechanism. The main advantages of these CMOS-compatible devices are the very low current drainage, as well as their multi-scale tunability and high precision. Devices based on this concept enable the creation of very low energy consumption circuits for computing deep neural network (DNN) models, where each DNPU has a projected over 100 Tera-operations per second per Watt.
This promising concept still requires further research, as it can be developed in diverse ways. From disparate materials (host and dopants) to distinct dopant concentrations, different surface sizes or the number of electrodes, as well as different combinations of data-input, control and readout electrodes. Also, there are different ways in which DNPU-based circuits could be scaled up, and having to create hardware circuits from scratch is an arduous and time-consuming process. The main purpose of the framework presented in this article is to facilitate research related to DNPUs (or similar nano-scale materials) and their scaling, by allowing the simulation of different multi-DNPU designs, and seamlessly validating them on real hardware. The main purpose is to be able to create Pytorch-like models based on DNPU circuits and apply them to resolve deep learning tasks, in a very similar way to how it would be done with Pytorch.
This wiki contains information about the installation process, package description, instructions for developers, basic usage examples, and troubleshooting for common issues that might occur. For other simple and more advanced examples of how to use this library, you can refer to https://github.com/BraiNEdarwin/brainspy-tasks, where you will find an implementation of the boolean gates [5] task and the ring classification task [6], as well as a set of Jupiter notebooks that will guide you through more complex examples, such as implementing a DNPU version of LeNet for resolving MNIST, using PyTorch and PyTorch lightning.
This introduction wiki explains some of the relevant concepts that are useful to understand the purpose of this library. Including the explanation of the three main packages used for this framework. For more information please refer to the publications available on the readme.
A Dopant Network Processing Unit (DNPU) is a novel concept for an electronic material that can exhibit a highly tunable non-linear direct current. A DNPU can be fabricated using a semiconductor as a host (e.g., Silicon) which is lightly doped (positive or negative type) with a conductive material (e.g., Boron). This combination of materials can be fabricated in a nano-scale active region in contact with several electrodes. When a voltage is applied to some of these electrodes, the dopants in the active region form an atomic-scale network through which the electrons can hop from one electrode to another, causing a non-linear current to flow in the remaining electrodes. The relationship between the voltage(s) and current(s) is non-linearly dependent.
Electrodes in a DNPU can be classified into the following groups:
- Activation electrodes: These electrodes receive input voltages (V) that will be used to obtain a non-linear output. The input range for these electrodes typically ranges from -1.2 to 0.7. Outside these outputs, the resulting output signal can become noisy [1]. In the image below, activation electrodes range from e0 to e6. These electrodes can be of two types:
- Data input electrodes: The data from a particular task that wants to be resolved. For example, if the intention was to make the DNPU behave as an XOR boolean gate, two data input electrodes could be used for receiving the combination of all possible input signals (00, 01, 10, and 11) [1]. In the image below, data input electrodes are e2 and e1.
- Control electrodes: The electrodes that will be used in order to control that the output signals behave as desired when trying to resolve a particular task. For example, if the intention was to make the DNPU behave as an XOR boolean gate, these electrodes would control the output signal in such a way that it exhibits the outputs 0, 1, 1, 0, for each of the inputs 00, 01, 10, and 11 respectively. In the image below, control electrodes are e0, e3, e4, e5, and e6.
- Readout electrodes: The resulting current (in nA) is measured using these electrodes. In the image below, the readout electrode is e_out
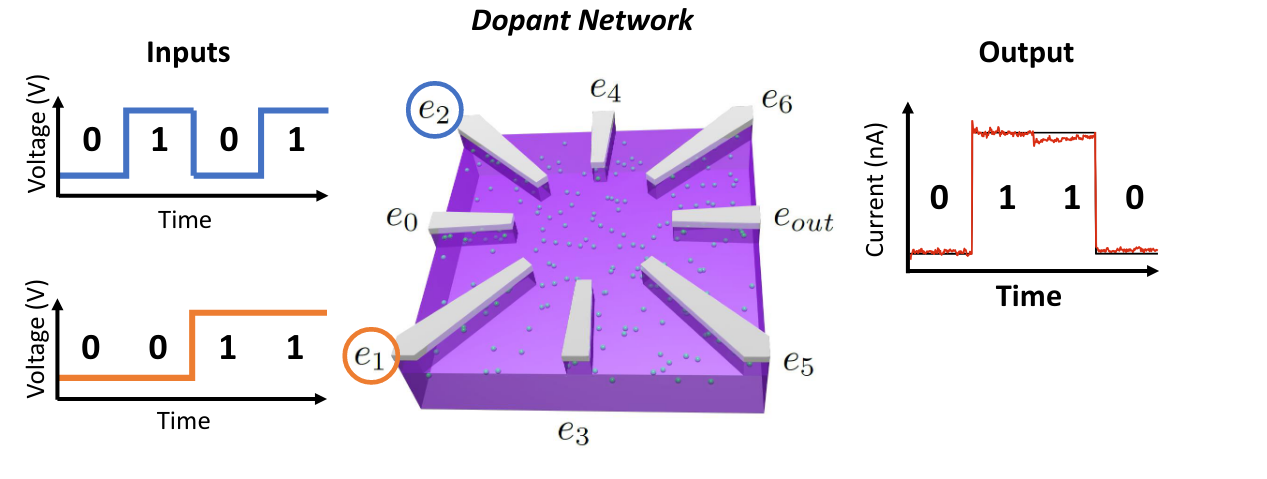
The principle of a DNPU can be exploited in different ways, as different materials can be used as dopant or host and the number of electrodes can vary. This package supports the exploration of functionality using DNPUs, regardless of their material, and/or their number of electrodes. More information on the concept of DNPUs and some of their applications can be found in [1][2]. Below, is an artistic representation of a DNPU with eight electrodes fabricated with Silicon and Boron.
In order to tune the output current(s) for a particular purpose, the device can be trained. The training process consists of searching the optimal control voltages such that the DNPU exhibits the desired non-linearity for a particular task (e.g., making the device behave as an XOR boolean gate). Once the optimal control voltage values are found, these can always be used to make a particular DNPU behave in a particular way. The DNPU is expected to maintain the same control voltages for a particular task over time.
A single DNPU can be trained using the following algorithms:
- Genetic Algorithm: In computer science and operations research, a genetic algorithm (GA) is a meta-heuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on bio-inspired operators such as mutation, crossover, and selection. This algorithm is suitable for experiments with reservoir computing [2].
- Gradient Descent: Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient (or approximate gradient) of the function at the current point. If, instead, one takes steps proportional to the positive of the gradient, one approaches a local maximum of that function; the procedure is then known as gradient ascent [3].
For a single DNPU, both algorithms can be applied in the following flavours:
-
On-chip: It enables to find adequate control voltages for a task measuring directly a hardware DNPU. Gradient descent in materio is not yet fully implemented and supported on brains-py. More information about this technique can be found in [4].
-
Off-chip: More information about this technique can be found in [1][2]. It consists of three main stages:
- Creating a surrogate model that simulates the input-to-output relationship of the electrodes of a given DNPU. The surrogate model can be created using the Surrogate Model Generator (SMG) repository [2]. This is divided into two main stages:
- The input-output data is gathered from the hardware DNPU by measuring it using one of our hardware setups.
- With the input-output data, a deep neural network is trained using the Pytorch library.
-
Finding adequate control voltages on simulation. The parameters of the deep neural network simulating the DNPU are frozen. The different control voltages applied to the control electrodes are declared as learnable parameters. The adequate control voltages are found using any of the gradient descent optimisation techniques offered by Pytorch. Save the PyTorch model with adequate control voltages. This training can happen on any computer, as long as it supports running the code of this repository.
-
Validate the results on the hardware DNPU. The saved model can be loaded on one of the setup computers. The configurations of the setup can be loaded into the new model. The model can be seamlessly run on the hardware, without having to program anything on top.
The off-chip training flavour simulates the input-to-output relationship of the electrodes of a DNPU using a deep neural network. The input data is gathered from the hardware DNPU using one of our hardware setups. The neural network simulating the DNPU is trained using the Pytorch library on the Surrogate Model Generator (SMG) repository [2]. Once the simulation model is produced, its parameters are frozen, and the control voltages applied to the model are declared as learnable parameters. Using different models of DNPUs, and taking advantage of the modules provided by the PyTorch library, the code from this repository can be used to quickly simulate circuits consisting of one or more DNPUs. The circuits can be trained using any of the different gradient descent techniques provided by Pytorch.
This framework enables the exploration of different mathematical operations, corresponding to circuit operations that can be applied to the outputs of DNPU models, helping to find different possible hardware designs for DNPU architectures. Additionally, the framework helps to save models and enables seamlessly validating the results obtained on the different hardware setups by reproducing the information stored in these models.
You can find more information on how to design multi-DNPU circuits on the Package description and User instructions and usage examples.
The brains-py code is divided into three main repositories, as represented in the image below.
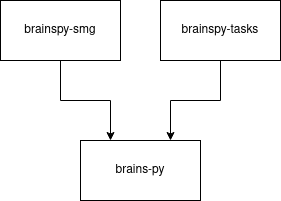
-
brains-py: It is the main repository of the family. It provides a set of drivers to connect to different hardware setups that are based on National Instruments hardware, enabling it to send and receive data from DNPU devices. The main purpose of this package is to help design multi-DNPU hardware solutions using off-chip gradient descent techniques. By using PyTorch nn.Module implementations as surrogate models, and different multi-DNPU circuits can be tried on simulations and validated on real hardware. The package includes an example of a gradient descent algorithm that can be used to find off-chip solutions on DNPU models. In addition, the package offers an on-chip genetic algorithm for a single DNPU. It also offers several custom loss/fitness functions, and a set of utils to control waveforms, loading YAML configs, linear current-to-voltage transformations, and creation of folders for experiments. This package heavily depends on having a surrogate model of a DNPU. This data is obtained using the brainspy-smg package.
-
brainspy-smg: Stands for surrogate model generator (SMG). This package helps gather the input-output relationship of the DNPU by generating an optimal input, based on sinusoidal or triangular modulated input signals. The ratio of frequencies is made irrational by choosing frequencies that are proportional to the square root of prime numbers, guaranteeing a good coverage of the input voltage space and preventing any recurrence of voltage combinations. This is further explained in [1]. The brainspy-smg package also helps with the creation of a surrogate model out of this data, and the corresponding info dictionary that helps log other features of the DNPU. Finally, the package also offers some utils to check the consistency of the DNPU data acquired as well as for testing IV curves of the device.
-
brainspy-tasks: It helps training DNPUs for two main benchmark tasks: boolean gates problem [5], and the ring classification problem [1][6]. It can help resolve these tasks using a genetic algorithm, for a single device off- or on-chip, or with gradient descent, for single or multiple devices using off-chip gradient descent. It is an example on how brains-py can be used to solve some benchmarking problems.
Brains-py can be installed on any computer for simulation purposes, following the Installation instructions. The only requirement to do simulations of single or multi DNPUs, is to have a surrogate model of a DNPU, which can be created using the surrogate model generator (brainspy-smg).
On the other hand, brains-py can also be installed for measuring DNPU hardware. Such installation would enable the gathering of data for the surrogate model, and also to validate off-chip solutions found during simulations. Current setups require to have a National Instruments device for interacting with the DNPU circuits. Any device that is compatible with the nidaqmx should also be compatible with the drivers of this repository. We currently operate using different setups with different instruments. You can request a list of the used setups by contacting the supporters of this repository.
This section covers certain terms used for the setups, which is useful to understand when using the configurations for the drivers of brains-py.
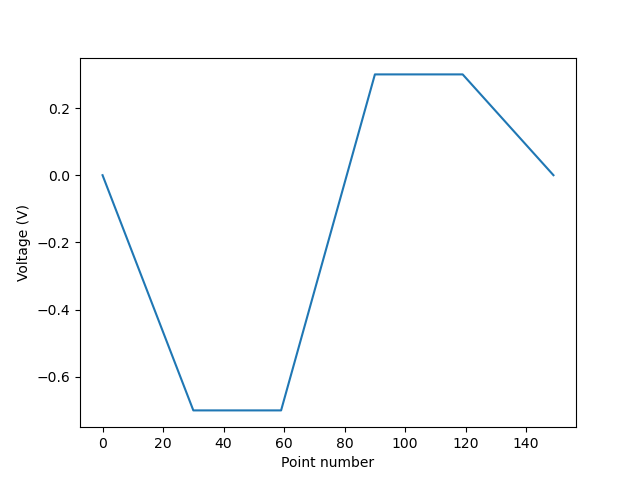
Although experiments have been done at room temperature [5], the typical operation of DNPU devices is at 77 Kelvin. This requires a structure that holds the DNPU in a cryogenic liquid. This can make the device be connected via long cables that are dipped into the liquid. The long cables can create some capacitive effects that can cause undesirable spikes on the device. In order to avoid sending signals with abrupt changes, and to ensure a safe operation, the use of waveforms is recommended. A waveform is a way of representing points that minimises abrupt changes. A waveform consists of slopes and plateaus. In order to represent two voltage points (e.g. -0.7 V, 0.3 V) a slope is created from zero to the initial point (-0.7). Then, the point is maintained for an amount of time with a plateau, then, another slope is created from -0.7 V to 0.3 V. Again, the value 0.3 V is maintained in a plateau, and finally, a slope reduces the voltage from 0.3 V to 0 V. The time used for the signal is dependent on the sampling frequency of the setup. It might be the case that some setups need more or fewer points at their max speed. It might also be that you are using a setup that requires no ramping and no plateaus.
The figure below shows the representation of the points -0.7 V and 0.3 V as a waveform with 30 points of slope length and 30 points of plateau length.
The drivers of brains-py support different types of National Instruments setups, as listed below:
-
cDAQ to niDAQ: This setup works by sending a spiking signal through an extra connection channel (cable) to synchronise the sending of a signal from a CDAQ module and its reception at a niDAQ instrument.
-
cDAQ to cDAQ: These setups are composed of several cDAQ modules inserted in a cDAQ Chassis (rack). There are two types of setups:
-
Regular: This setup is connected to a PC, that controls the sending of signals.
-
Real-Time: This setup can run a real-time operating system, enabling to have stand-alone operations. The drivers of brains-py also support using a PC to send signals.
All of the drivers for national instruments have been created using the official nidaqmx library for python.
-
The output current of the DNPU device is typically in a magnitude of nano-Amperes. It is typically passed through an operational amplifier, which amplifies the current and transforms it into a voltage [5] (Supplementary Material). In order to retrieve the original current value, the output that is read by the cDAQ or niDAQ modules needs to be multiplied by an amplification correction factor. This amplification is unique to each PCB circuit used for measuring the DNPU devices, and it can be calculated with the feedback resistance value (R_f) of the operational amplifier, by multiplying the voltage by 1/R_f. It is assumed that the value coming out of this operation is in nano-Amperes. If the real value would be calculated, it would have to be multiplied by 10^9.
Some of the PCBs used in connection with National Instruments devices apply an inversion of the signal after passing it through an operational amplifier. The drivers of brains-py allow to invert this signal back in those cases.
[1] HC Ruiz Euler, MN Boon, JT Wildeboer, B van de Ven, T Chen, H Broersma, PA Bobbert, WG van der Wiel (2020). A Deep-Learning Approach to Realising Functionality in Nanoelectronic Devices. https://doi.org/10.1038/s41565-020-00779-y
[2] Mitchell, Melanie (1996). An Introduction to Genetic Algorithms. Cambridge, MA: MIT Press. ISBN 9780585030944
[3] https://en.wikipedia.org/wiki/Gradient_descent
[4] MN Boon, HC Ruiz Euler, T Chen, B van de Ven, U Alegre Ibarra, PA. Bobbert, WG van der Wiel. Gradient descent in materio. https://arxiv.org/abs/2105.11233
[5] Chen, T., van Gelder, J., van de Ven, B., Amitonov, S. V., de Wilde, B., Euler, H. C. R., ... & van der Wiel, W. G. (2020). Classification with a disordered dopant-atom network in silicon. Nature, 577(7790), 341-345. https://doi.org/10.1038/s41586-019-1901-0
[6] HCR Euler, U Alegre-Ibarra, B van de Ven, H Broersma, PA Bobbert and WG van der Wiel (2020). Dopant Network Processing Units: Towards Efficient Neural-network Emulators with High-capacity Nanoelectronic Nodes. https://arxiv.org/abs/2007.12371