###k-d Trees
It can be difficult to run calculations and algorithms on an unsorted (or difficult to sort) set of data points (spatial data, for instance). Here's an example: let's say I give you a list of all restaurants in San Francisco (with their locations), and then ask you to tell me all the restaurants within 4 blocks of our current location. Naively, we might think we have to search through every single restaurant in the list to find our answer. Turns out there's a better approach.
A k-d tree (specifically a quadtree) can help. A k-d tree is a data structure that allows us to search sortable data very quickly.
####Binary Search Trees
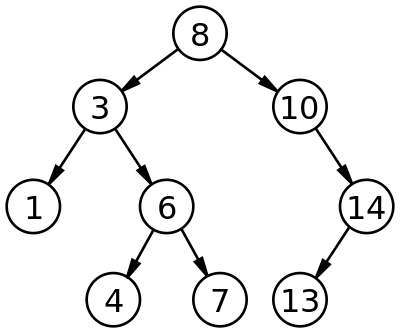
Let’s start with the binary search tree. A binary search tree is a data structure where each node contains one value and two children-- left and right. Every node on the left branch of a binary search tree is less than the original node's value, and anything to the right is greater.
Binary search trees allow us to search one dimensional space very efficiently. Rather than searching through every value to determine if something exists in the set, we can start from the top of the BST, and make steps that each cut our search space in half. In the above diagram, if we’re looking to see if 4 is in the tree, we start at the top node (8), and move to the left, so we never even see that 10, 14, and 13 exist. Then we move to the right from 3, ignoring the 1. Finally, we move to the left from 6, and see that the 4 is, in fact, in the tree. To determine that 4 was in the tree, we only had to check the value of four nodes, rather than all nine. You can repeat the same logic to determine that a node doesn't exist. (for instance, we can find that 9 isn’t in the tree by examining only 2 nodes)
This technique of dividing the search space is extremely powerful, as it reduces the time complexity of search operations from linear to logarithmic.
This strategy can be applied to sorted trees with two dimensions, as well. We can, instead of holding a single value at each node, hold a set of coordinates. This models two dimensional space (think of a cartesian grid). By holding x, y coordinates at each node, we can split the rest of the space into four quadrants-- everything above and to the right, above and left, below and left, and the last quadrant with points below and to the right of the node. We can keep inserting more coordinates into this system by determining which quadrant they belong in, and adding them as children of the parent nodes, then additional nodes as children of those nodes, so on. Then when we want to search for something, we again do not have to search through all data points, but only the ones in the right search space. We can even search within a range of points, if we wanted to search within some two dimensional range.
####k-d Trees
Turns out this strategy can be applied to any number of dimensions (say z, or time) and still have the same benefit of dividing the search space. It gets harder to visualize above 3 dimensions, but you can imagine the benefit of dividing data according to this scheme for any number of dimensions you have.
####Back to the problem...
Now that we have a good data structure to hold all our restaurant coordinates, it becomes much faster to find everything within a four block radius of us. We start at the first node (hopefully somewhere around the center of the city), and quickly cut down our search space, potentially cutting out 75% of the search space with each decision we make. Using this approach, we'll quickly get our list of restaurants nearby.
There are other uses of k-d trees than just finding restaurants, of course. Collision detection could be done using a quadtree, and you can imagine how facebook can determine which of your friends are nearby using a k-d tree, as well. What other uses can you think of?