树.md

created_at	updated_at	slug
2023-02-06 13:32:12 -0800	2023-02-06 13:32:12 -0800	data-structure-tree

日常讨论最多的树基本上都是查找树，构建、调整树的目的，都是为了快速地查找。在有限的资源下，谁能够在树的构建和查找上取得更加均衡的性能，谁就会成为最常用的技术。这里说的有限资源，主要是指存储：内存或磁盘。

如果数据集较少，只需要在内存中操作，主要考虑构建和查找树的时间复杂度，这类树的优胜者是红黑树；如果数据集很大，如GB级别，内存不足以存储整个数据集，势必以磁盘为主要存储手段，磁盘IO会是主要问题，减少IO操作是主要目的，这类树的优胜者是B+树。

严格地说，无论红黑树还是B+树，和平衡二叉树（AVL树）没有必然的联系，但考虑到树的平衡对查询的重要性，因此了解构建AVL树的详细步骤也是有必要的。

从树的构建思路上看，有自顶向下和自底向上两种方式。前者和我们最开始学习的树一脉相承，AVL树是自顶向下构建的典型代表；后者天然满足平衡性，且节点、合并的发生频率明显小于自顶向下构建的AVL树，典型代表是B树。

B树最开始被设计用于外部查询，即整颗树存储在磁盘上，在此基础上微调优化的B+树是数据库索引最常见的结构；基于B树自底向上的思想，简化发展出了对称二叉B树，用于内部查询；后又发展出更好理解的2-3-4树；基于2-3-4树推导出了易于实现的版本——红黑树。

AVL树

平衡二叉树，也叫AVL树，AVL得名于其发明者Adelson-Velsky and Landis Tree，并非平衡二叉树的英文缩写。记住它的两个特征即可

• 二叉，即每个节点最多有两个子节点
• 平衡，即每个节点的左子树和右子树高度差不超过1

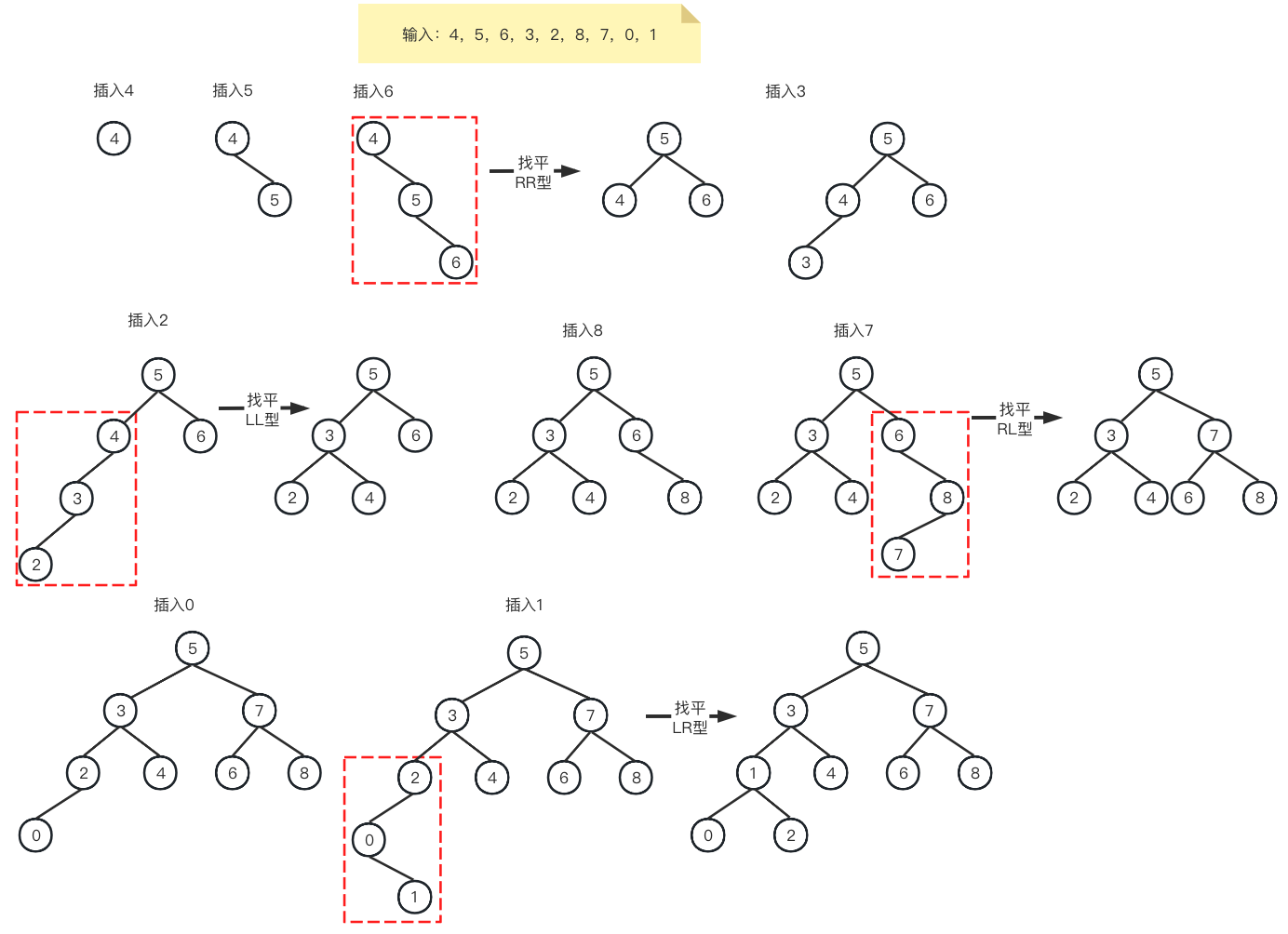
为了达成这两个特征，每插入新节点，都需要重新找平。一般认为有四种不平衡的情况，通过左旋、右旋操作完成找平。下面说明原理

• 由于每插入一个新节点都会找平，所以只需要调整的离插入节点最近的那颗不平衡子树

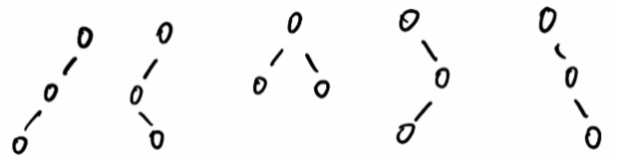
• 树的不平衡只与离根节点最近的三个节点有关，调整它们即可。三个节点，总共五种排列方式

  

  第三种平衡，其它四种不平衡，找平的目的就是将四种不平衡的情况转变为第三种情况

  这四种不平衡结构，从左到右我们称之为 LL、LR、RL、RR 型

• 给节点从上到下编号为 A B C；所谓调整，就是确立新的结构，并处理其父子节点关系。这四种情况分别如下调整

  • LL
    • B为新根，C为左节点，A为右节
    • B父=原A父；B左子=C；B有子=A
    • A父=B；A左子=原B右子；A右子=原A右子
    • C父=B；C左子=原C左子；C右子=原C右子
  • LR
    • C为新根，B为左节点，A为右节点
    • C父=原A父；C左子=B；C右子=A
    • B父=C；B左子=原B左子；B右子=原C左子
    • A父=C；A左子=原C右子；A右子=原A右子
  • RL
    • C为新根，A为左节点，B为右节点
    • C父=原A父；C左子A；C右子=B
    • A父=C；A左子=原A左子；A右子=原C左子
    • B父=C；B左子=原C右子；B右子=原B右子
  • RR
    • B为新根，A为左节点，C为右节点
    • B父=原A父；B左子=A；B右子=C
    • A父=B；A左子=原A左子；A右子=原B左子
    • C父=B；C左子=原C左子；C右子=原C右子

  上述步骤，可以直接转换为代码

理解如上的关键点即可，忽略其它文章和书籍所谓左旋右旋操作，它们只会带来误导。一个典型的AVL树构建过程如下

B树

B树的发明是用来组织和维护大型顺序索引的，大型索引必然存储在磁盘中，这种情况下磁盘IO是主要耗时因素。B树的解决办法是增加节点容量，降低树的高度。

B树有几个术语

• page：B树中一个节点就是一个page
• entry：一个page由多个entry构成，它们是有序的序列，一个entry包含如下属性
  • p：指向子节点的指针
  • x：被索引的key，比如数据库中对id做索引，那此处就是id
  • α：被索引内容的指针，对数据库而言，它可能是id对应的行的文件句柄

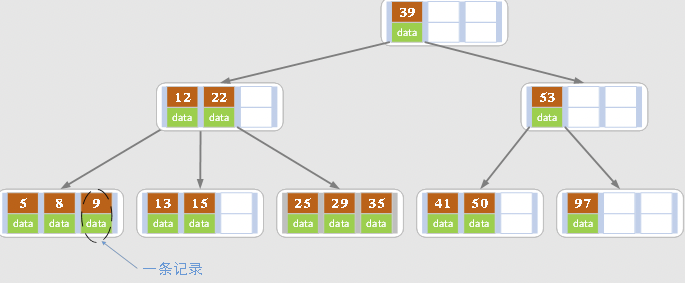
二者关系如下

网上找了一个B树的图，能够大致说明问题：数字代表x、data代表α、箭头根部代表p

相对平常的二叉树，B树有几个特点

• 是序列和树的结合体，树用于减少IO次数（在一个B树中，找到目标节点至多需要IO次数=树的高度）；序列用于在内存中查找
• 树的构建自底向上：新数据总是插入叶子结点，随着叶子节点数量超过2k+1，分裂成两个节点，并引入父节点。这样带来两个好处
  • 根节点到任何叶子结点的高度都是一样的，使得查询稳定
  • 插入简单，只有节点数量超过限制时才需要进行分裂操作，分裂过程也很简单（具体可以随便搜一篇文章，然后自己画一画）

B+树

B树已经能够解决外部索引问题了，但还有两个点可以优化，优化结果就是B+树，具体来说

• 树的高度能够进一步降低：将中间节点page的entry内的α去掉，转移到叶子节点，使得中间节点的entry更小，使得单个page能够存储更多entry，能够退出分裂到来的时间，从而减缓树高度的增长速度。进而减少IO
• 范围查询不是很方便：上一步一方面降低了树的高度，另一方面使得数据引用全部转移到了叶子节点，它们又是有序的，可以直接用链表串联它们，范围查询就非常方便

2-3-4树

B树中，节点拥有最多子节点的个数，称之为度，2-3-4树就是度为4的B树。也就是说，它具有B树最珍贵的两个特点

• 所有叶子结点到根节点距离一样，意味着这是一个平衡树。节点的查询时间和AVL树一样是logN，最坏的情况也只是节点内有三个key，使得查询时间复杂度为2logN，但从CPU角度来说，没有什么区别
• 插入简单，总体性能高于AVL树

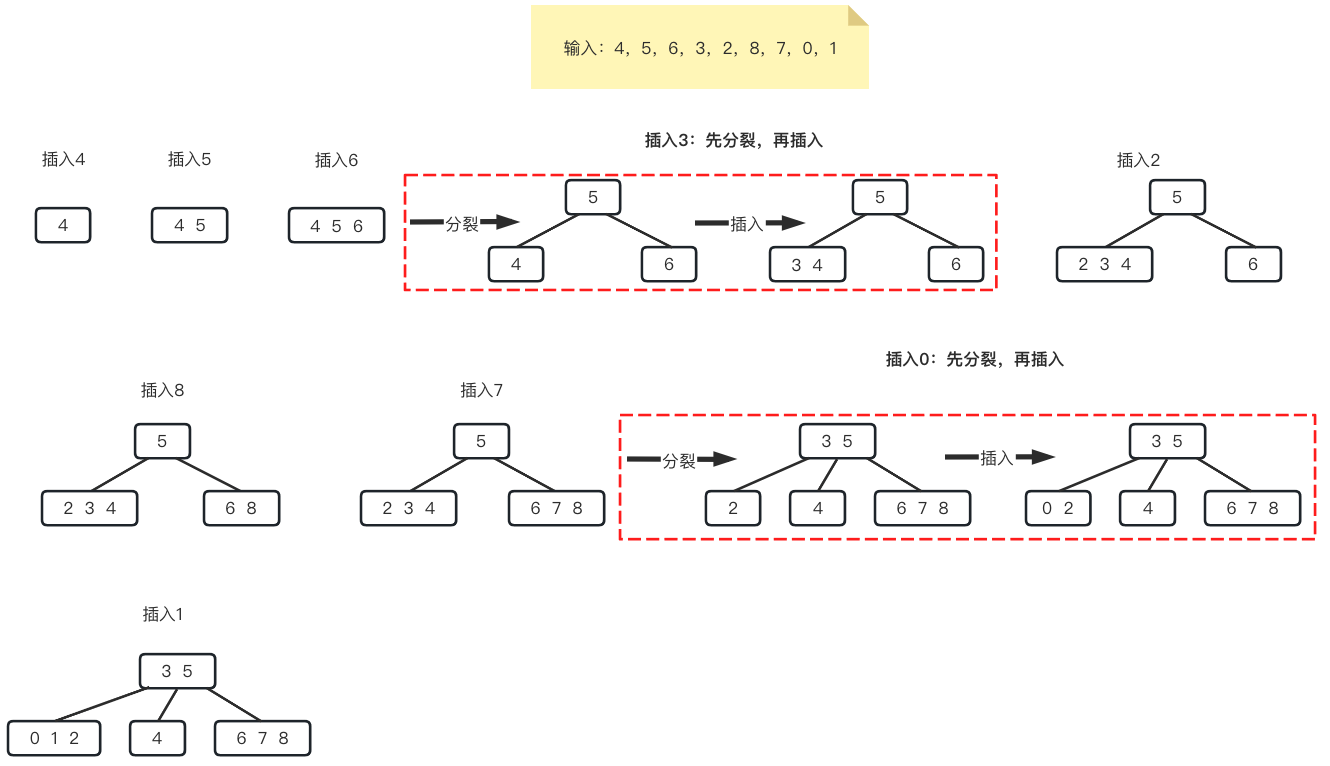
一个2-3-4树构建过程如下

和AVL树的构建相比，同样的输入，AVL树进行了4次调整操作（旋转）；而2-3-4树只进行了2次调整操作（分裂）。这要归功于高度节点的缓存作用。

为什么2-3-4树比AVL树高效

• 查询：上面已经说过了，查询上来说，AVL树是更高效的
• 增删：相对于AVL树，2-3-4树的3节点和4节点实际上起到对不平衡的缓存作用；不平衡时通过高度节点向低度节点转换；当增删足够随机时，高度节点的缓存效果越明显。使得增删效率明显高于AVL树。

增删少，查询多，用AVL树；增删多，用2-3-4树

红黑树

红黑树并不是直接发明出来的，而是2-3-4树的等效表示，目的是代码实现更加方便。可以直接将2-3-4树转换为红黑树

• 2节点不用管
• 3节点拆分为具有单个子节点的2节点，该左子节点标记为红色
• 4节点拆分为具有左右子节点的2节点，两个子节点都标记为红色

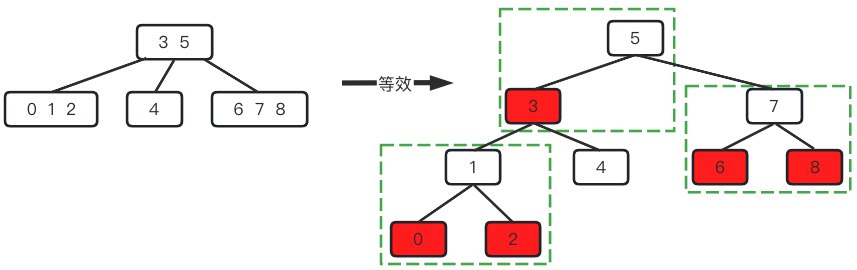
网上随便找了个图

将上一节中的2-3-4树转换为红黑树如下，绿色框表示它们原本在一个2-3-4树节点

总结

各种树的定义，过两天肯定会忘，所以本文没写，但要理解这些树的来源和用途，理解了才可能用到。过多地停留在定义只会浪费精力。

参考资料

• B树论文 - Organization and maintenance of large orderd indices
• 对称二叉B树论文 - Symmetric Binary B-Trees: Data Structure and Algorithms for Random and Sequential Information Processing
• 其它各种网络文章