-
Notifications
You must be signed in to change notification settings - Fork 32
/
5、模式分解.md
180 lines (97 loc) · 9.2 KB
/
5、模式分解.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
### 模式分解
#### 存在问题
模式分解
* 关系模式R(U)的分解是指用R的一组子集$\rho$={R1(U1),...,Rk(Uk)}来代替它。其中U= U1$\bigcup$U2$\bigcup$...$\bigcup$Uk;Ui$\nsubseteqq$Uj(i$\neq$j)。
* 注:为便于后面叙述,我们用Ri代替Ri(Ui), R代替R(U)。
对于关系模式R的任一关系r, 它向$\rho$的投影连接记为$m_\rho$(r)
* $m_\rho$(r) = $\prod_{R1}$(r) $\Join$...$\Join$$\prod_{Rk}$(r))= $\Join_{(i=1,...,k)}$$\prod_{Ri}$(
* 这里:$\prod_{Ri}$(r)={t[Ri] | t$\in$r, i=1,...,k }
模式分解需要关注:
* R与 $\rho$在数据内容方面是否等价:分解的无损连接性;
* R与 $\rho$在数据依赖方面是否等价:分解的保持依赖性。
[引理]:设R为一关系模式, $\rho$={R1,...,Rk}是R的一个分解,r是R的任一个关系,ri=$\prod_{Ri}$(r),则有规则成立:
* (rule 1):r$\subseteqq$$m_\rho$(r)
* 即:所有未分解前的关系,要包含在分解后重新连接得到的关系里
* (rule 2):若s = $m_\rho$(r), 则$\prod_{Ri}$(s) = ri(即:$\prod_{Ri}$($m_\rho$(r)) = $\prod_{Ri}$(r))
* 即:所有分解的关系,在连接后还能再分解会去
* (rule 3):$m_\rho$( $m_\rho$(r)) = $m_\rho$(r)
* 即:对连接后的关系再拿去让分解后的关系连接,仍然和原关系一样
#### 无损连接分解
无损连接分解
* 对于关系模式R(U, F), U是属性全集,F是函数依赖集合,$\rho$={R1,...,Rk}是R的一个分解,如果对于R的任何满足函数依赖集F的关系r, 有r= $m_\rho$(r),则称$\rho$是R相对于F的一个无损连接分解,其中:$m_\rho$(r) = $\prod_{R1}$(r) $\Join$...$\Join$$\prod_{Rk}$(r) = $\Join_{(i=1,...,k)}$$\prod_{Ri}$(r)
无损连接性检验算法
* Input:关系模式R=A1A2...An, 函数依赖集F, 分解$\rho$={R1,...,Rk}
* Output:$\rho$是否是无损连接的判断
* Method:
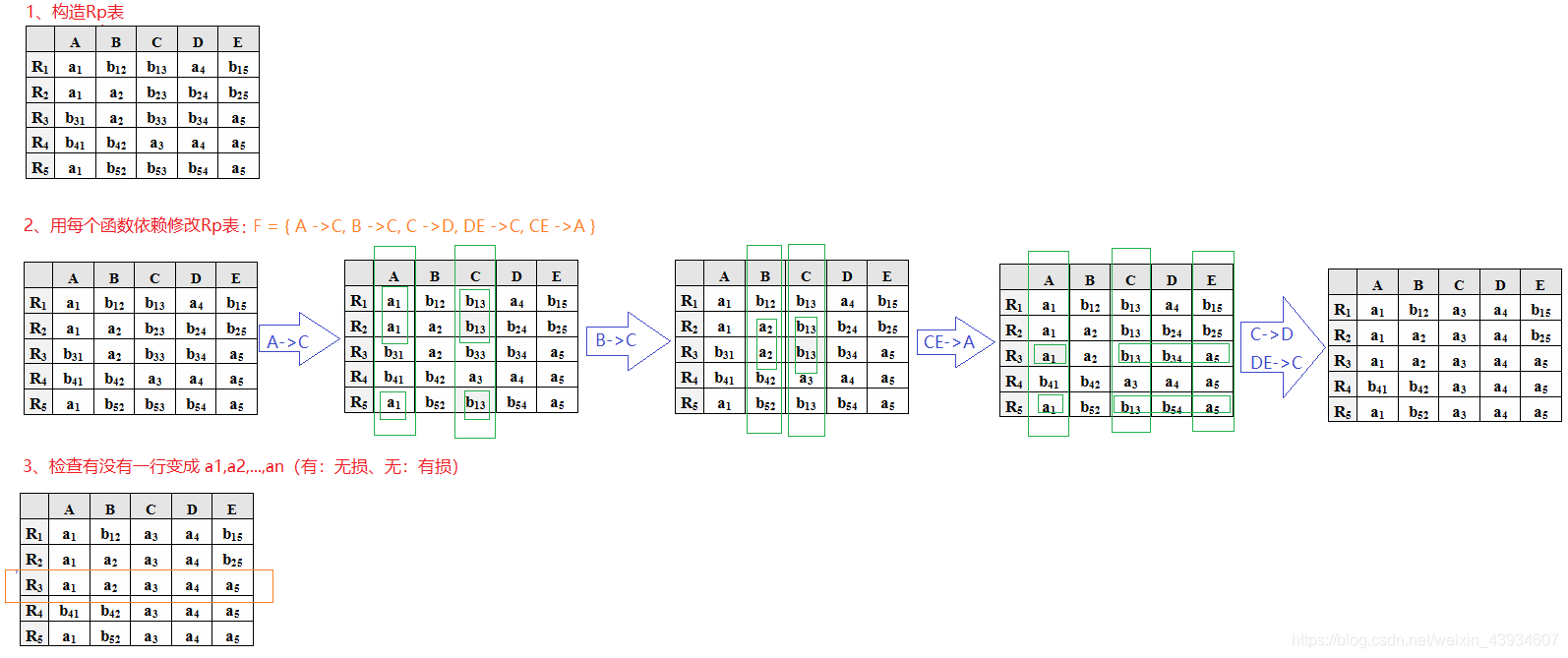
* (1) 构造一k行n列的表,可称为$R_{\rho}$表。其中第j列对应于Aj, 第i行对应于Ri, 若Aj$\in$Ri, 则$R_{\rho}$表中第i行第j列位置填写符号aj, 否则填写bij。
* (2) 根据$\forall$(X $\rightarrow$Y)$\in$F, 对$R_{\rho}$表进行修改:
* 给定X$\rightarrow$Y,在表中寻找对应于X中所有属性分量之列上符号全相同的行。
* 若能找到,则在这些行的对应于Y中属性的那些列上置相同符号:
* 若其中有一个行的相应列上为aj,则使其它行同一列上置aj;
* 若相应列上均为bij(或blj),则使其它行同一列上置某一个bij(或blj,任一个都可,只要相同);
* (3) 在上述修改的表中,如果发现有一行变成a1, a2,..., an(全a), 则$\rho$是无损连接分解,否则$\rho$是有损连接分解。
* 示例:已知 R={ ABCDE }、F = { A$\rightarrow$C, B$\rightarrow$C, C$\rightarrow$D, DE$\rightarrow$C, CE$\rightarrow$A }、$\rho$={R1(AD), R2(AB), R3(BE), R4(CDE), R5(AE)},问:$\rho$是否具有无损连接性?
[定理] 设F是关系模式R上的一个函数依赖集合。$\rho$={R1,R2}是R的一个分解,则:当且仅当R1$\bigcap$R2$\rightarrow$R1$-$R2 或者 R1$\bigcap$R2$\rightarrow$R2$-$R1属于F+时,$\rho$是关于F无损连接的。
* 证明:由前述算法证明

#### 保持依赖分解
保持依赖分解
* 对于关系模式R(U, F), U是属性全集,F是函数依赖集合,$\rho$={R1,...,Rk}是R的一个分解,如在$\prod_{Ri}$(F)中的所有依赖之并集(i=1,...,k)逻辑蕴涵F的每个依赖,则称分解$\rho$保持依赖集F。其中$\prod_{Ri}$(F)是F在Ri上的投影,即F中的任一投影X $\rightarrow$Y,如果X, Y均包含于Ri,则X$\rightarrow$Y$\in$$\prod_{Ri}$(F)。Ri指Ri的属性集。
* 注:
* (1) 保持依赖的分解可能不是无损连接的。
* (2) 无损连接的分解可能不是保持依赖的。
* 示例:
* R(CSZ), F={ CS$\rightarrow$Z, Z$\rightarrow$C }, C是城市,S是街区, Z是邮政编码,$\rho$={R1(SZ), R2(CZ)}为一无损连接分解,但却不保持依赖;
* R(ABCD), F={A$\rightarrow$B, C$\rightarrow$D}, $\rho$={R1(AB), R2(CD)}为一保持依赖分解,但不是无损连接分解。
保持依赖性检验算法
* Input:关系模式R=A1A2...An, R上的函数依赖集F, 分解$\rho$={R1,...,Rk}
* Output:$\rho$是否是保持依赖的判断
* Method:令G = $\bigcup_{(i=1 to k)}$$\prod_{Ri}$, 只需检查G是否覆盖F即可。具体算法如下:
* 首先对每个X$\rightarrow$Y$\in$F计算G中的$X^+_G$:(如果X不包含于Ri则不需计算了)
Z = X
WHILE Z的变化发生 DO
FOR i =1 to k DO
Z = Z $\bigcup$(${(Z \bigcap Ri)}^+$ $\bigcap$ Ri)
* 判断G是否逻辑蕴涵X$\rightarrow$Y:前面计算的结果Z便是X+, 如果Z包含Y, 则G逻辑蕴涵X$\rightarrow$Y,否则便不逻辑蕴涵。
* 判断$\rho$是否保持依赖:如果G逻辑蕴涵F中的每一个函数依赖,则说$\rho$是保持依赖的分解,否则便不是保持依赖的分解。
示例
* Input:R(A, B, C, D, E)、F = { A$\rightarrow$C, B$\rightarrow$C, C$\rightarrow$D, DE$\rightarrow$C, CE$\rightarrow$A } 、$\rho$={R1(AC), R2(BC), R3(CDE) }
* Output:$\rho$ 是否是保持依赖的判断
* Method:依据题意$\prod_{R1}$(F)={ A $\rightarrow$C }, $\prod_{R2}$(F)={ B $\rightarrow$C } , $\prod_{R3}$(F)={ C $\rightarrow$D , DE $\rightarrow$C },G = { A $\rightarrow$C , B $\rightarrow$C , C $\rightarrow$D , DE $\rightarrow$C } ,显然不保持依赖。
* 对函数依赖A $\rightarrow$C$\in$F计算G中的$X^+_G$:Z = {A } $\bigcup${ C }$\bigcup${ } $\bigcup${ }={A,C}, C包含于Z中,所以A$\rightarrow$C被G逻辑蕴涵
* 对函数依赖DE $\rightarrow$C$\in$F计算G中的$X^+_G$:Z = {D,E}$\bigcup${ } $\bigcup${ } $\bigcup${ C, D }={C,D, E}, C包含于Z中,所以A$\rightarrow$C被G逻辑蕴涵
* 对函数依赖CE $\rightarrow$A$\in$F计算G中的$X^+_G$:Z = {C, E } $\bigcup${ } $\bigcup${ } $\bigcup${D } = {C, E, D}, A不包含于Z中,所以不被G逻辑蕴涵
#### 分解成3NF或BCNF
无损连接分解成BCNF的算法
* Input:关系模式R(U, F)
* Output:R的一个无损连接分解$\rho$,$\rho$中的每个关系模式都是F在该模式上投影的BCNF。
* Method:
* (1) 令$\rho$={ R }。
* (2) 对每个模式s$\in$$\rho$, 若s$\notin$BCNF, 则s上必有X $\rightarrow$A成立且X不是s的超键且A$\notin$X,此时用模式s1, s2替代$\rho$中的模式s,其中s1由A和X构成,s2由s中除A以外的所有属性构成(可以发现,s1$\in$BCNF)。
* (3) 重复步骤(2), 直至$\rho$中全部关系模式达到BCNF。
* 注:本算法不能保证一关系模式分解成BCNF而又保持依赖。
* 证明:无损分解最后给出的定理。
* 示例:R(A, B, C, D, E, F, G)函数依赖集合{ A $\rightarrow$B, A $\rightarrow$C, C $\rightarrow$D, C $\rightarrow$E, E $\rightarrow$FG }
* 候选键:A; 有不依赖于候选键的其他函数依赖,R不满足BCNF。
* 分解规则:
* 将左侧不含候选键的函数依赖单独组成一个关系, 将包含候选键的组成一关系$\rho$={ R1(A, B, C), R2(CDEFG) }
* 分解 R2 ,候选键为 C,把不含 C 的关系作为 R3 : R2(CDE)、R3(EFG)
* 可以看出:R1 $\in$BCNF; R2 $\in$BCNF; R3 $\in$BCNF;
保持依赖分解成3NF的算法。
* Input:关系模式R(U, F), F是函数依赖集最小覆盖。
* Output:R的一个保持依赖分解$\rho$,$\rho$中的每个关系模式都是F在该模式上投影的3NF。
* Method:
* (1) 把R中不出现在F中的属性去掉并单独组成一模式。
* (2) 对$\forall$X$\rightarrow$A$\in$F, 则以XA组成一模式; 若有X $\rightarrow$A1, X $\rightarrow$A2,..., X $\rightarrow$Am都属于F, 则以XA1A2...Am组成一模式(即将n个模式合并为一个模式)。
* (3)取$\rho$为上述模式之集合,则$\rho$即为所求之分解。
* 示例:R(A, B, C, D, E, F, G)函数依赖集合{ A $\rightarrow$B, A $\rightarrow$C, C $\rightarrow$D, C $\rightarrow$E, E $\rightarrow$FG }
* 候选键:A; 有传递依赖,R不满足3NF。
* 分解规则:将每一个函数依赖单独组成一个关系$\rho$={ R1(A, B), R2(A, C), R3(C, D) , R4(C, E) , R5(E, F, G) }
* 可以看出:每一个模式都属于3NF, 且$\rho$是保持依赖的
* 也可以合并一些关系:$\rho$={ R12(A, B, C), R34(C, D, E) , R5(E, F, G) }
既保持依赖又无损连接
* 设$\sigma$是按前述算法构造的R的一个第三范式分解,X是R的候选键,则:$\tau$= $\sigma$$\bigcup${ X }将是R的一个分解,且该分解中的所有关系模式是第三范式的,$\tau$有保持依赖和无损连接性。
* 即按照保持依赖方法分解后,把候选键相同的合并即可
* 示例:R(A, B, C, D, E, F, G),函数依赖:A$\rightarrow$B, A$\rightarrow$C, C$\rightarrow$D, C$\rightarrow$E, E$\rightarrow$FG
* 保持依赖的分解成3NF然后合并:$\rho$={ R12(A, B, C), R34(C, D, E) , R5(E, F, G) }