参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
《代码随想录》算法视频公开课:你对二叉搜索树了解的还不够! | LeetCode:98.验证二叉搜索树,相信结合视频再看本篇题解,更有助于大家对本题的理解。
要知道中序遍历下,输出的二叉搜索树节点的数值是有序序列。
有了这个特性,验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。
可以递归中序遍历将二叉搜索树转变成一个数组,代码如下:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val); // 将二叉搜索树转换为有序数组
traversal(root->right);
}然后只要比较一下,这个数组是否是有序的,注意二叉搜索树中不能有重复元素。
traversal(root);
for (int i = 1; i < vec.size(); i++) {
// 注意要小于等于,搜索树里不能有相同元素
if (vec[i] <= vec[i - 1]) return false;
}
return true;整体代码如下:
class Solution {
private:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val); // 将二叉搜索树转换为有序数组
traversal(root->right);
}
public:
bool isValidBST(TreeNode* root) {
vec.clear(); // 不加这句在leetcode上也可以过,但最好加上
traversal(root);
for (int i = 1; i < vec.size(); i++) {
// 注意要小于等于,搜索树里不能有相同元素
if (vec[i] <= vec[i - 1]) return false;
}
return true;
}
};以上代码中,我们把二叉树转变为数组来判断,是最直观的,但其实不用转变成数组,可以在递归遍历的过程中直接判断是否有序。
这道题目比较容易陷入两个陷阱:
- 陷阱1
不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了。
写出了类似这样的代码:
if (root->val > root->left->val && root->val < root->right->val) {
return true;
} else {
return false;
}我们要比较的是 左子树所有节点小于中间节点,右子树所有节点大于中间节点。所以以上代码的判断逻辑是错误的。
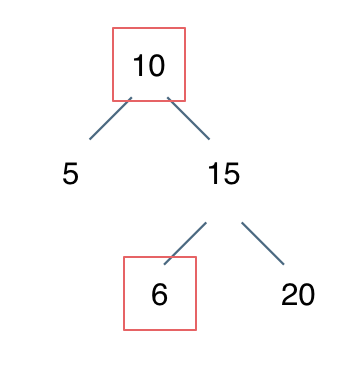
例如: [10,5,15,null,null,6,20] 这个case:
节点10大于左节点5,小于右节点15,但右子树里出现了一个6 这就不符合了!
- 陷阱2
样例中最小节点 可能是int的最小值,如果这样使用最小的int来比较也是不行的。
此时可以初始化比较元素为longlong的最小值。
问题可以进一步演进:如果样例中根节点的val 可能是longlong的最小值 又要怎么办呢?文中会解答。
了解这些陷阱之后我们来看一下代码应该怎么写:
递归三部曲:
- 确定递归函数,返回值以及参数
要定义一个longlong的全局变量,用来比较遍历的节点是否有序,因为后台测试数据中有int最小值,所以定义为longlong的类型,初始化为longlong最小值。
注意递归函数要有bool类型的返回值, 我们在二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值? 中讲了,只有寻找某一条边(或者一个节点)的时候,递归函数会有bool类型的返回值。
其实本题是同样的道理,我们在寻找一个不符合条件的节点,如果没有找到这个节点就遍历了整个树,如果找到不符合的节点了,立刻返回。
代码如下:
long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
bool isValidBST(TreeNode* root)- 确定终止条件
如果是空节点 是不是二叉搜索树呢?
是的,二叉搜索树也可以为空!
代码如下:
if (root == NULL) return true;- 确定单层递归的逻辑
中序遍历,一直更新maxVal,一旦发现maxVal >= root->val,就返回false,注意元素相同时候也要返回false。
代码如下:
bool left = isValidBST(root->left); // 左
// 中序遍历,验证遍历的元素是不是从小到大
if (maxVal < root->val) maxVal = root->val; // 中
else return false;
bool right = isValidBST(root->right); // 右
return left && right;整体代码如下:
class Solution {
public:
long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
// 中序遍历,验证遍历的元素是不是从小到大
if (maxVal < root->val) maxVal = root->val;
else return false;
bool right = isValidBST(root->right);
return left && right;
}
};以上代码是因为后台数据有int最小值测试用例,所以都把maxVal改成了longlong最小值。
如果测试数据中有 longlong的最小值,怎么办?
不可能在初始化一个更小的值了吧。 建议避免 初始化最小值,如下方法取到最左面节点的数值来比较。
代码如下:
class Solution {
public:
TreeNode* pre = NULL; // 用来记录前一个节点
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
if (pre != NULL && pre->val >= root->val) return false;
pre = root; // 记录前一个节点
bool right = isValidBST(root->right);
return left && right;
}
};最后这份代码看上去整洁一些,思路也清晰。
可以用迭代法模拟二叉树中序遍历,对前中后序迭代法生疏的同学可以看这两篇二叉树:听说递归能做的,栈也能做!,二叉树:前中后序迭代方式统一写法
迭代法中序遍历稍加改动就可以了,代码如下:
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL; // 记录前一个节点
while (cur != NULL || !st.empty()) {
if (cur != NULL) {
st.push(cur);
cur = cur->left; // 左
} else {
cur = st.top(); // 中
st.pop();
if (pre != NULL && cur->val <= pre->val)
return false;
pre = cur; //保存前一个访问的结点
cur = cur->right; // 右
}
}
return true;
}
};在二叉树:二叉搜索树登场!中我们分明写出了痛哭流涕的简洁迭代法,怎么在这里不行了呢,因为本题是要验证二叉搜索树啊。
这道题目是一个简单题,但对于没接触过的同学还是有难度的。
所以初学者刚开始学习算法的时候,看到简单题目没有思路很正常,千万别怀疑自己智商,学习过程都是这样的,大家智商都差不多。
只要把基本类型的题目都做过,总结过之后,思路自然就开阔了,加油💪
//使用統一迭代法
class Solution {
public boolean isValidBST(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
if(root != null)
stack.add(root);
while(!stack.isEmpty()){
TreeNode curr = stack.peek();
if(curr != null){
stack.pop();
if(curr.right != null)
stack.add(curr.right);
stack.add(curr);
stack.add(null);
if(curr.left != null)
stack.add(curr.left);
}else{
stack.pop();
TreeNode temp = stack.pop();
if(pre != null && pre.val >= temp.val)
return false;
pre = temp;
}
}
return true;
}
}class Solution {
// 递归
TreeNode max;
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
// 左
boolean left = isValidBST(root.left);
if (!left) {
return false;
}
// 中
if (max != null && root.val <= max.val) {
return false;
}
max = root;
// 右
boolean right = isValidBST(root.right);
return right;
}
}
class Solution {
// 迭代
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;// 左
}
// 中,处理
TreeNode pop = stack.pop();
if (pre != null && pop.val <= pre.val) {
return false;
}
pre = pop;
root = pop.right;// 右
}
return true;
}
}
// 简洁实现·递归解法
class Solution {
public boolean isValidBST(TreeNode root) {
return validBST(Long.MIN_VALUE, Long.MAX_VALUE, root);
}
boolean validBST(long lower, long upper, TreeNode root) {
if (root == null) return true;
if (root.val <= lower || root.val >= upper) return false;
return validBST(lower, root.val, root.left) && validBST(root.val, upper, root.right);
}
}
// 简洁实现·中序遍历
class Solution {
private long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
if (!isValidBST(root.left)) {
return false;
}
if (root.val <= prev) { // 不满足二叉搜索树条件
return false;
}
prev = root.val;
return isValidBST(root.right);
}
}递归法(版本一)利用中序递增性质,转换成数组
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.vec = []
def traversal(self, root):
if root is None:
return
self.traversal(root.left)
self.vec.append(root.val) # 将二叉搜索树转换为有序数组
self.traversal(root.right)
def isValidBST(self, root):
self.vec = [] # 清空数组
self.traversal(root)
for i in range(1, len(self.vec)):
# 注意要小于等于,搜索树里不能有相同元素
if self.vec[i] <= self.vec[i - 1]:
return False
return True递归法(版本二)设定极小值,进行比较
class Solution:
def __init__(self):
self.maxVal = float('-inf') # 因为后台测试数据中有int最小值
def isValidBST(self, root):
if root is None:
return True
left = self.isValidBST(root.left)
# 中序遍历,验证遍历的元素是不是从小到大
if self.maxVal < root.val:
self.maxVal = root.val
else:
return False
right = self.isValidBST(root.right)
return left and right递归法(版本三)直接取该树的最小值
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.pre = None # 用来记录前一个节点
def isValidBST(self, root):
if root is None:
return True
left = self.isValidBST(root.left)
if self.pre is not None and self.pre.val >= root.val:
return False
self.pre = root # 记录前一个节点
right = self.isValidBST(root.right)
return left and right
迭代法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root):
stack = []
cur = root
pre = None # 记录前一个节点
while cur is not None or len(stack) > 0:
if cur is not None:
stack.append(cur)
cur = cur.left # 左
else:
cur = stack.pop() # 中
if pre is not None and cur.val <= pre.val:
return False
pre = cur # 保存前一个访问的结点
cur = cur.right # 右
return Truefunc isValidBST(root *TreeNode) bool {
// 二叉搜索树也可以是空树
if root == nil {
return true
}
// 由题目中的数据限制可以得出min和max
return check(root,math.MinInt64,math.MaxInt64)
}
func check(node *TreeNode,min,max int64) bool {
if node == nil {
return true
}
if min >= int64(node.Val) || max <= int64(node.Val) {
return false
}
// 分别对左子树和右子树递归判断,如果左子树和右子树都符合则返回true
return check(node.Right,int64(node.Val),max) && check(node.Left,min,int64(node.Val))
}// 中序遍历解法
func isValidBST(root *TreeNode) bool {
// 保存上一个指针
var prev *TreeNode
var travel func(node *TreeNode) bool
travel = func(node *TreeNode) bool {
if node == nil {
return true
}
leftRes := travel(node.Left)
// 当前值小于等于前一个节点的值,返回false
if prev != nil && node.Val <= prev.Val {
return false
}
prev = node
rightRes := travel(node.Right)
return leftRes && rightRes
}
return travel(root)
}辅助数组解决
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isValidBST = function (root) {
let arr = [];
const buildArr = (root) => {
if (root) {
buildArr(root.left);
arr.push(root.val);
buildArr(root.right);
}
}
buildArr(root);
for (let i = 1; i < arr.length; ++i) {
if (arr[i] <= arr[i - 1])
return false;
}
return true;
};递归中解决
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
let pre = null;
var isValidBST = function (root) {
let pre = null;
const inOrder = (root) => {
if (root === null)
return true;
let left = inOrder(root.left);
if (pre !== null && pre.val >= root.val)
return false;
pre = root;
let right = inOrder(root.right);
return left && right;
}
return inOrder(root);
};迭代法:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
let pre = null;
var isValidBST = function (root) {
const queue = [];
let cur = root;
let pre = null;
while (cur !== null || queue.length !== 0) {
if (cur !== null) {
queue.push(cur);
cur = cur.left;
} else {
cur = queue.pop();
if (pre !== null && cur.val <= pre.val) {
return false;
}
pre = cur;
cur = cur.right;
}
}
return true;
};辅助数组解决:
function isValidBST(root: TreeNode | null): boolean {
const traversalArr: number[] = [];
function inorderTraverse(root: TreeNode | null): void {
if (root === null) return;
inorderTraverse(root.left);
traversalArr.push(root.val);
inorderTraverse(root.right);
}
inorderTraverse(root);
for (let i = 0, length = traversalArr.length; i < length - 1; i++) {
if (traversalArr[i] >= traversalArr[i + 1]) return false;
}
return true;
};递归中解决:
function isValidBST(root: TreeNode | null): boolean {
let maxVal = -Infinity;
function inorderTraverse(root: TreeNode | null): boolean {
if (root === null) return true;
let leftValid: boolean = inorderTraverse(root.left);
if (!leftValid) return false;
if (maxVal < root.val) {
maxVal = root.val
} else {
return false;
}
let rightValid: boolean = inorderTraverse(root.right);
return leftValid && rightValid;
}
return inorderTraverse(root);
};迭代法:
function isValidBST(root: TreeNode | null): boolean {
const queue: TreeNode[] = [];
let cur: TreeNode | null = root;
let pre: TreeNode | null = null;
while (cur !== null || queue.length !== 0) {
if (cur !== null) {
queue.push(cur);
cur = cur.left;
} else {
cur = queue.pop()!;
if (pre !== null && cur!.val <= pre.val) {
return false;
}
pre = cur;
cur = cur!.right;
}
}
return true;
}辅助数组解决:
object Solution {
import scala.collection.mutable
def isValidBST(root: TreeNode): Boolean = {
var arr = new mutable.ArrayBuffer[Int]()
// 递归中序遍历二叉树,将节点添加到arr
def traversal(node: TreeNode): Unit = {
if (node == null) return
traversal(node.left)
arr.append(node.value)
traversal(node.right)
}
traversal(root)
// 这个数组如果是升序就代表是二叉搜索树
for (i <- 1 until arr.size) {
if (arr(i) <= arr(i - 1)) return false
}
true
}
}递归中解决:
object Solution {
def isValidBST(root: TreeNode): Boolean = {
var flag = true
var preValue:Long = Long.MinValue // 这里要使用Long类型
def traversal(node: TreeNode): Unit = {
if (node == null || flag == false) return
traversal(node.left)
if (node.value > preValue) preValue = node.value
else flag = false
traversal(node.right)
}
traversal(root)
flag
}
}递归:
impl Solution {
pub fn is_valid_bst(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
Self::valid_bst(i64::MIN, i64::MAX, root)
}
pub fn valid_bst(low: i64, upper: i64, root: Option<Rc<RefCell<TreeNode>>>) -> bool {
if root.is_none() {
return true;
}
let root = root.as_ref().unwrap().borrow();
if root.val as i64 <= low || root.val as i64 >= upper {
return false;
}
Self::valid_bst(low, root.val as i64, root.left.clone())
&& Self::valid_bst(root.val as i64, upper, root.right.clone())
}
}辅助数组:
impl Solution {
pub fn is_valid_bst(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
let mut vec = vec![];
Self::valid_bst(root, &mut vec);
for i in 1..vec.len() {
if vec[i] <= vec[i - 1] {
return false;
}
}
true
}
pub fn valid_bst(root: Option<Rc<RefCell<TreeNode>>>, mut v: &mut Vec<i64>) {
if root.is_none() {
return;
}
let node = root.as_ref().unwrap().borrow();
Self::valid_bst(node.left.clone(), v);
v.push(node.val as i64);
Self::valid_bst(node.right.clone(), v);
}
}// 递归
public long val = Int64.MinValue;
public bool IsValidBST(TreeNode root)
{
if (root == null) return true;
bool left = IsValidBST(root.left);
if (root.val > val) val = root.val;
else return false;
bool right = IsValidBST(root.right);
return left && right;
}