README_EN.md

comments	difficulty	edit_url	tags
true	Easy	https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3200.Maximum%20Height%20of%20a%20Triangle/README_EN.md	Array Enumeration

3200. Maximum Height of a Triangle

中文文档

Description

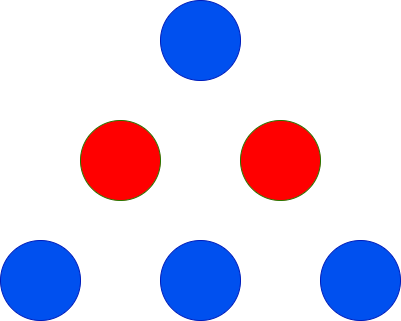
You are given two integers red and blue representing the count of red and blue colored balls. You have to arrange these balls to form a triangle such that the 1^st row will have 1 ball, the 2^nd row will have 2 balls, the 3^rd row will have 3 balls, and so on.

All the balls in a particular row should be the same color, and adjacent rows should have different colors.

Return the maximum height of the triangle that can be achieved.

 

Example 1:

Input: red = 2, blue = 4

Output: 3

Explanation:

The only possible arrangement is shown above.

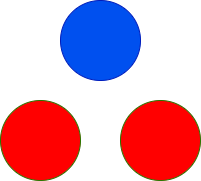
Example 2:

Input: red = 2, blue = 1

Output: 2

Explanation:

The only possible arrangement is shown above.

Example 3:

Input: red = 1, blue = 1

Output: 1

Example 4:

Input: red = 10, blue = 1

Output: 2

Explanation:

The only possible arrangement is shown above.

 

Constraints:

• 1 <= red, blue <= 100

Solutions

Solution 1: Simulation

We can enumerate the color of the first row, then simulate the construction of the triangle, calculating the maximum height.

The time complexity is $O(\sqrt{n})$, where $n$ is the number of red and blue balls. The space complexity is $O(1)$.

Python3

class Solution:
    def maxHeightOfTriangle(self, red: int, blue: int) -> int:
        ans = 0
        for k in range(2):
            c = [red, blue]
            i, j = 1, k
            while i <= c[j]:
                c[j] -= i
                j ^= 1
                ans = max(ans, i)
                i += 1
        return ans

Java

class Solution {
    public int maxHeightOfTriangle(int red, int blue) {
        int ans = 0;
        for (int k = 0; k < 2; ++k) {
            int[] c = {red, blue};
            for (int i = 1, j = k; i <= c[j]; j ^= 1, ++i) {
                c[j] -= i;
                ans = Math.max(ans, i);
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maxHeightOfTriangle(int red, int blue) {
        int ans = 0;
        for (int k = 0; k < 2; ++k) {
            int c[2] = {red, blue};
            for (int i = 1, j = k; i <= c[j]; j ^= 1, ++i) {
                c[j] -= i;
                ans = max(ans, i);
            }
        }
        return ans;
    }
};

Go

func maxHeightOfTriangle(red int, blue int) (ans int) {
	for k := 0; k < 2; k++ {
		c := [2]int{red, blue}
		for i, j := 1, k; i <= c[j]; i, j = i+1, j^1 {
			c[j] -= i
			ans = max(ans, i)
		}
	}
	return
}

TypeScript

function maxHeightOfTriangle(red: number, blue: number): number {
    let ans = 0;
    for (let k = 0; k < 2; ++k) {
        const c: [number, number] = [red, blue];
        for (let i = 1, j = k; i <= c[j]; ++i, j ^= 1) {
            c[j] -= i;
            ans = Math.max(ans, i);
        }
    }
    return ans;
}