| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
Medium |
1756 |
Biweekly Contest 128 Q3 |
|
There is an undirected graph of n nodes. You are given a 2D array edges, where edges[i] = [ui, vi, lengthi] describes an edge between node ui and node vi with a traversal time of lengthi units.
Additionally, you are given an array disappear, where disappear[i] denotes the time when the node i disappears from the graph and you won't be able to visit it.
Notice that the graph might be disconnected and might contain multiple edges.
Return the array answer, with answer[i] denoting the minimum units of time required to reach node i from node 0. If node i is unreachable from node 0 then answer[i] is -1.
Example 1:
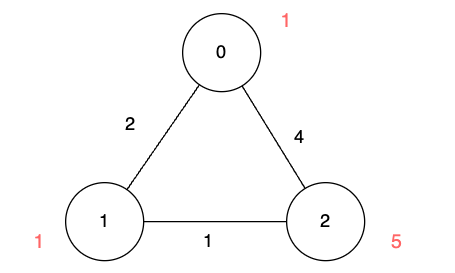
Input: n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,1,5]
Output: [0,-1,4]
Explanation:
We are starting our journey from node 0, and our goal is to find the minimum time required to reach each node before it disappears.
- For node 0, we don't need any time as it is our starting point.
- For node 1, we need at least 2 units of time to traverse
edges[0]. Unfortunately, it disappears at that moment, so we won't be able to visit it. - For node 2, we need at least 4 units of time to traverse
edges[2].
Example 2:
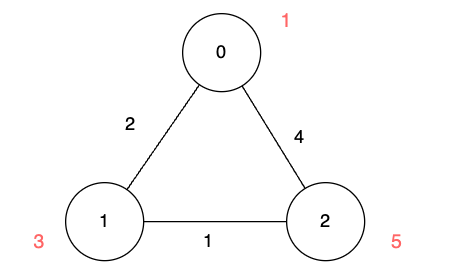
Input: n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,3,5]
Output: [0,2,3]
Explanation:
We are starting our journey from node 0, and our goal is to find the minimum time required to reach each node before it disappears.
- For node 0, we don't need any time as it is the starting point.
- For node 1, we need at least 2 units of time to traverse
edges[0]. - For node 2, we need at least 3 units of time to traverse
edges[0]andedges[1].
Example 3:
Input: n = 2, edges = [[0,1,1]], disappear = [1,1]
Output: [0,-1]
Explanation:
Exactly when we reach node 1, it disappears.
Constraints:
1 <= n <= 5 * 1040 <= edges.length <= 105edges[i] == [ui, vi, lengthi]0 <= ui, vi <= n - 11 <= lengthi <= 105disappear.length == n1 <= disappear[i] <= 105
First, we create an adjacency list
Then, we use Dijkstra's algorithm to calculate the shortest distance from node
- Create a priority queue
$q$ to store the distance and node number of nodes. Initially, add node$0$ to the queue with a distance of$0$ . - Take out a node
$u$ from the queue. If the distance$du$ of$u$ is greater than$dist[u]$ , it means that$u$ has been updated, so skip it directly. - Traverse all neighbor nodes
$v$ of node$u$ . If$dist[v] > dist[u] + w$ and$dist[u] + w < disappear[v]$ , then update$dist[v] = dist[u] + w$ and add node$v$ to the queue. - Repeat steps 2 and 3 until the queue is empty.
Finally, we traverse the
The time complexity is
class Solution:
def minimumTime(
self, n: int, edges: List[List[int]], disappear: List[int]
) -> List[int]:
g = defaultdict(list)
for u, v, w in edges:
g[u].append((v, w))
g[v].append((u, w))
dist = [inf] * n
dist[0] = 0
q = [(0, 0)]
while q:
du, u = heappop(q)
if du > dist[u]:
continue
for v, w in g[u]:
if dist[v] > dist[u] + w and dist[u] + w < disappear[v]:
dist[v] = dist[u] + w
heappush(q, (dist[v], v))
return [a if a < b else -1 for a, b in zip(dist, disappear)]class Solution {
public int[] minimumTime(int n, int[][] edges, int[] disappear) {
List<int[]>[] g = new List[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : edges) {
int u = e[0], v = e[1], w = e[2];
g[u].add(new int[] {v, w});
g[v].add(new int[] {u, w});
}
int[] dist = new int[n];
Arrays.fill(dist, 1 << 30);
dist[0] = 0;
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
pq.offer(new int[] {0, 0});
while (!pq.isEmpty()) {
var e = pq.poll();
int du = e[0], u = e[1];
if (du > dist[u]) {
continue;
}
for (var nxt : g[u]) {
int v = nxt[0], w = nxt[1];
if (dist[v] > dist[u] + w && dist[u] + w < disappear[v]) {
dist[v] = dist[u] + w;
pq.offer(new int[] {dist[v], v});
}
}
}
int[] ans = new int[n];
for (int i = 0; i < n; ++i) {
ans[i] = dist[i] < disappear[i] ? dist[i] : -1;
}
return ans;
}
}class Solution {
public:
vector<int> minimumTime(int n, vector<vector<int>>& edges, vector<int>& disappear) {
vector<vector<pair<int, int>>> g(n);
for (const auto& e : edges) {
int u = e[0], v = e[1], w = e[2];
g[u].push_back({v, w});
g[v].push_back({u, w});
}
vector<int> dist(n, 1 << 30);
dist[0] = 0;
using pii = pair<int, int>;
priority_queue<pii, vector<pii>, greater<pii>> pq;
pq.push({0, 0});
while (!pq.empty()) {
auto [du, u] = pq.top();
pq.pop();
if (du > dist[u]) {
continue;
}
for (auto [v, w] : g[u]) {
if (dist[v] > dist[u] + w && dist[u] + w < disappear[v]) {
dist[v] = dist[u] + w;
pq.push({dist[v], v});
}
}
}
vector<int> ans(n);
for (int i = 0; i < n; ++i) {
ans[i] = dist[i] < disappear[i] ? dist[i] : -1;
}
return ans;
}
};func minimumTime(n int, edges [][]int, disappear []int) []int {
g := make([][]pair, n)
for _, e := range edges {
u, v, w := e[0], e[1], e[2]
g[u] = append(g[u], pair{v, w})
g[v] = append(g[v], pair{u, w})
}
dist := make([]int, n)
for i := range dist {
dist[i] = 1 << 30
}
dist[0] = 0
pq := hp{{0, 0}}
for len(pq) > 0 {
du, u := pq[0].dis, pq[0].u
heap.Pop(&pq)
if du > dist[u] {
continue
}
for _, nxt := range g[u] {
v, w := nxt.dis, nxt.u
if dist[v] > dist[u]+w && dist[u]+w < disappear[v] {
dist[v] = dist[u] + w
heap.Push(&pq, pair{dist[v], v})
}
}
}
ans := make([]int, n)
for i := 0; i < n; i++ {
if dist[i] < disappear[i] {
ans[i] = dist[i]
} else {
ans[i] = -1
}
}
return ans
}
type pair struct{ dis, u int }
type hp []pair
func (h hp) Len() int { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].dis < h[j].dis }
func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any) { *h = append(*h, v.(pair)) }
func (h *hp) Pop() any { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }