comments

difficulty

edit_url

rating

source

3108. 带权图里旅途的最小代价

English Version

题目描述

给你一个 n 个节点的带权无向图，节点编号为 0 到 n - 1 。

给你一个整数 n 和一个数组 edges ，其中 edges[i] = [u_i, v_i, w_i] 表示节点 u_i 和 v_i 之间有一条权值为 w_i 的无向边。

在图中，一趟旅途包含一系列节点和边。旅途开始和结束点都是图中的节点，且图中存在连接旅途中相邻节点的边。注意，一趟旅途可能访问同一条边或者同一个节点多次。

如果旅途开始于节点 u ，结束于节点 v ，我们定义这一趟旅途的代价是经过的边权按位与 AND 的结果。换句话说，如果经过的边对应的边权为 w₀, w₁, w₂, ..., w_k ，那么代价为w₀ & w₁ & w₂ & ... & w_k ，其中 & 表示按位与 AND 操作。

给你一个二维数组 query ，其中 query[i] = [s_i, t_i] 。对于每一个查询，你需要找出从节点开始 s_i ，在节点 t_i 处结束的旅途的最小代价。如果不存在这样的旅途，答案为 -1 。

返回数组 answer ，其中 answer[i] 表示对于查询 i 的最小旅途代价。

示例 1：

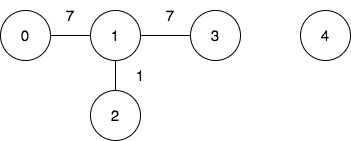
输入：n = 5, edges = [[0,1,7],[1,3,7],[1,2,1]], query = [[0,3],[3,4]]

输出：[1,-1]

解释：

第一个查询想要得到代价为 1 的旅途，我们依次访问：0->1（边权为 7 ）1->2 （边权为 1 ）2->1（边权为 1 ）1->3 （边权为 7 ）。

第二个查询中，无法从节点 3 到节点 4 ，所以答案为 -1 。

示例 2：

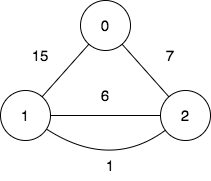
输入：n = 3, edges = [[0,2,7],[0,1,15],[1,2,6],[1,2,1]], query = [[1,2]]

输出：[0]

解释：

第一个查询想要得到代价为 0 的旅途，我们依次访问：1->2（边权为 1 ），2->1（边权为 6 ），1->2（边权为 1 ）。

提示：

1 <= n <= 10⁵
0 <= edges.length <= 10⁵
edges[i].length == 3
0 <= u_i, v_i <= n - 1
u_i != v_i
0 <= w_i <= 10⁵
1 <= query.length <= 10⁵
query[i].length == 2
0 <= s_i, t_i <= n - 1

解法

方法一：贪心 + 并查集

我们注意到，一个正整数与其他若干个正整数不断进行“按位与”运算，结果只会越来越小。因此，为了使得旅途的代价尽可能小，我们应该将处于同一个连通分量的所有边的权值进行“按位与”运算，然后再进行查询。

那么，问题转化为，如何找出同一个连通份量的所有边，然后进行“按位与”运算。

我们可以用并查集来维护连通分量。

具体地，我们遍历每一条边 $(u, v, w)$，将 $u$ 和 $v$ 进行合并。然后，我们再一次遍历每一条边 $(u, v, w)$，找到 $u$ 和 $v$ 所在的连通分量的根节点 $root$，用一个数组 $g$ 记录每个连通分量的所有边的权值进行“按位与”运算的结果。

最后，对于每一个查询 $(s, t)$，我们首先判断 $s$ 与 $t$ 是否相等，如果相等，那么答案为 $0$，否则，我们判断 $s$ 和 $t$ 是否在同一个连通分量中，如果在同一个连通分量中，那么答案为该查询的连通分量的根节点的 $g$ 值，否则，答案为 $-1$。

时间复杂度 $O((n + m + q) \times \alpha(n))$，空间复杂度 $O(n)$。其中 $n$, $m$ 和 $q$ 分别表示节点数、边数和查询数，而 $\alpha(n)$ 表示 Ackermann 函数的反函数。

Python3

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.size = [1] * n

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, a, b):
        pa, pb = self.find(a), self.find(b)
        if pa == pb:
            return False
        if self.size[pa] > self.size[pb]:
            self.p[pb] = pa
            self.size[pa] += self.size[pb]
        else:
            self.p[pa] = pb
            self.size[pb] += self.size[pa]
        return True


class Solution:
    def minimumCost(
        self, n: int, edges: List[List[int]], query: List[List[int]]
    ) -> List[int]:
        g = [-1] * n
        uf = UnionFind(n)
        for u, v, _ in edges:
            uf.union(u, v)
        for u, _, w in edges:
            root = uf.find(u)
            g[root] &= w

        def f(u: int, v: int) -> int:
            if u == v:
                return 0
            a, b = uf.find(u), uf.find(v)
            return g[a] if a == b else -1

        return [f(s, t) for s, t in query]

Java

class UnionFind {
    private final int[] p;
    private final int[] size;

    public UnionFind(int n) {
        p = new int[n];
        size = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
            size[i] = 1;
        }
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    public boolean union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            return false;
        }
        if (size[pa] > size[pb]) {
            p[pb] = pa;
            size[pa] += size[pb];
        } else {
            p[pa] = pb;
            size[pb] += size[pa];
        }
        return true;
    }

    public int size(int x) {
        return size[find(x)];
    }
}

class Solution {
    private UnionFind uf;
    private int[] g;

    public int[] minimumCost(int n, int[][] edges, int[][] query) {
        uf = new UnionFind(n);
        for (var e : edges) {
            uf.union(e[0], e[1]);
        }
        g = new int[n];
        Arrays.fill(g, -1);
        for (var e : edges) {
            int root = uf.find(e[0]);
            g[root] &= e[2];
        }
        int m = query.length;
        int[] ans = new int[m];
        for (int i = 0; i < m; ++i) {
            int s = query[i][0], t = query[i][1];
            ans[i] = f(s, t);
        }
        return ans;
    }

    private int f(int u, int v) {
        if (u == v) {
            return 0;
        }
        int a = uf.find(u), b = uf.find(v);
        return a == b ? g[a] : -1;
    }
}

C++

class UnionFind {
public:
    UnionFind(int n) {
        p = vector<int>(n);
        size = vector<int>(n, 1);
        iota(p.begin(), p.end(), 0);
    }

    bool unite(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            return false;
        }
        if (size[pa] > size[pb]) {
            p[pb] = pa;
            size[pa] += size[pb];
        } else {
            p[pa] = pb;
            size[pb] += size[pa];
        }
        return true;
    }

    int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    int getSize(int x) {
        return size[find(x)];
    }

private:
    vector<int> p, size;
};

class Solution {
public:
    vector<int> minimumCost(int n, vector<vector<int>>& edges, vector<vector<int>>& query) {
        g = vector<int>(n, -1);
        uf = new UnionFind(n);
        for (auto& e : edges) {
            uf->unite(e[0], e[1]);
        }
        for (auto& e : edges) {
            int root = uf->find(e[0]);
            g[root] &= e[2];
        }
        vector<int> ans;
        for (auto& q : query) {
            ans.push_back(f(q[0], q[1]));
        }
        return ans;
    }

private:
    UnionFind* uf;
    vector<int> g;

    int f(int u, int v) {
        if (u == v) {
            return 0;
        }
        int a = uf->find(u), b = uf->find(v);
        return a == b ? g[a] : -1;
    }
};

Go

type unionFind struct {
	p, size []int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	size := make([]int, n)
	for i := range p {
		p[i] = i
		size[i] = 1
	}
	return &unionFind{p, size}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) bool {
	pa, pb := uf.find(a), uf.find(b)
	if pa == pb {
		return false
	}
	if uf.size[pa] > uf.size[pb] {
		uf.p[pb] = pa
		uf.size[pa] += uf.size[pb]
	} else {
		uf.p[pa] = pb
		uf.size[pb] += uf.size[pa]
	}
	return true
}

func (uf *unionFind) getSize(x int) int {
	return uf.size[uf.find(x)]
}

func minimumCost(n int, edges [][]int, query [][]int) (ans []int) {
	uf := newUnionFind(n)
	g := make([]int, n)
	for i := range g {
		g[i] = -1
	}
	for _, e := range edges {
		uf.union(e[0], e[1])
	}
	for _, e := range edges {
		root := uf.find(e[0])
		g[root] &= e[2]
	}
	f := func(u, v int) int {
		if u == v {
			return 0
		}
		a, b := uf.find(u), uf.find(v)
		if a == b {
			return g[a]
		}
		return -1
	}
	for _, q := range query {
		ans = append(ans, f(q[0], q[1]))
	}
	return
}

TypeScript

class UnionFind {
    p: number[];
    size: number[];
    constructor(n: number) {
        this.p = Array(n)
            .fill(0)
            .map((_, i) => i);
        this.size = Array(n).fill(1);
    }

    find(x: number): number {
        if (this.p[x] !== x) {
            this.p[x] = this.find(this.p[x]);
        }
        return this.p[x];
    }

    union(a: number, b: number): boolean {
        const [pa, pb] = [this.find(a), this.find(b)];
        if (pa === pb) {
            return false;
        }
        if (this.size[pa] > this.size[pb]) {
            this.p[pb] = pa;
            this.size[pa] += this.size[pb];
        } else {
            this.p[pa] = pb;
            this.size[pb] += this.size[pa];
        }
        return true;
    }

    getSize(x: number): number {
        return this.size[this.find(x)];
    }
}

function minimumCost(n: number, edges: number[][], query: number[][]): number[] {
    const uf = new UnionFind(n);
    const g: number[] = Array(n).fill(-1);
    for (const [u, v, _] of edges) {
        uf.union(u, v);
    }
    for (const [u, _, w] of edges) {
        const root = uf.find(u);
        g[root] &= w;
    }
    const f = (u: number, v: number): number => {
        if (u === v) {
            return 0;
        }
        const [a, b] = [uf.find(u), uf.find(v)];
        return a === b ? g[a] : -1;
    };
    return query.map(([u, v]) => f(u, v));
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

3108. 带权图里旅途的最小代价

题目描述

解法

方法一：贪心 + 并查集

Python3

Java

C++

Go

TypeScript

Files

README.md

Latest commit

History

README.md

File metadata and controls

3108. 带权图里旅途的最小代价

题目描述

解法

方法一：贪心 + 并查集

Python3

Java

C++

Go

TypeScript