Skip to content

Latest commit

 

History

History
217 lines (178 loc) · 8.84 KB

README.md

File metadata and controls

217 lines (178 loc) · 8.84 KB
Raw
comments difficulty edit_url rating source tags
true
中等
1601
第 386 场周赛 Q2
几何
数组
数学

3047. 求交集区域内的最大正方形面积

English Version

题目描述

在二维平面上存在 n 个矩形。给你两个下标从 0 开始的二维整数数组 bottomLeft 和 topRight，两个数组的大小都是 n x 2 ，其中 bottomLeft[i] 和 topRight[i] 分别代表第 i 个矩形的 左下角 和 右上角 坐标。

我们定义 向右 的方向为 x 轴正半轴（x 坐标增加），向左 的方向为 x 轴负半轴（x 坐标减少）。同样地，定义 向上 的方向为 y 轴正半轴（y 坐标增加），向下 的方向为 y 轴负半轴（y 坐标减少）。

你可以选择一个区域，该区域由两个矩形的 交集 形成。你需要找出能够放入该区域 内 的 最大 正方形面积，并选择最优解。

返回能够放入交集区域的正方形的 最大 可能面积，如果矩形之间不存在任何交集区域，则返回 0。

 

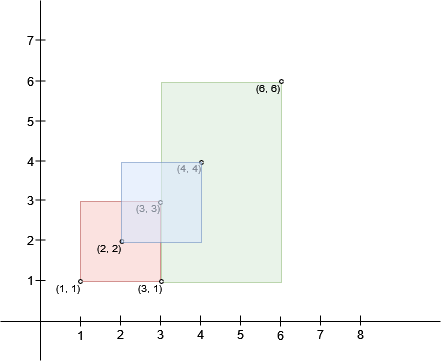
示例 1：

输入：bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]
输出：1
解释：边长为 1 的正方形可以放入矩形 0 和矩形 1 的交集区域，或矩形 1 和矩形 2 的交集区域。因此最大面积是边长 * 边长，即 1 * 1 = 1。
可以证明，边长更大的正方形无法放入任何交集区域。

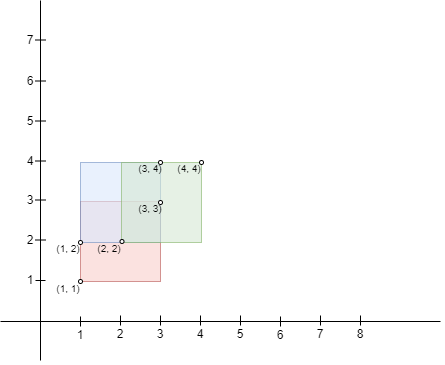
示例 2：

输入：bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]
输出：1
解释：边长为 1 的正方形可以放入矩形 0 和矩形 1，矩形 1 和矩形 2，或所有三个矩形的交集区域。因此最大面积是边长 * 边长，即 1 * 1 = 1。
可以证明，边长更大的正方形无法放入任何交集区域。
请注意，区域可以由多于两个矩形的交集构成。

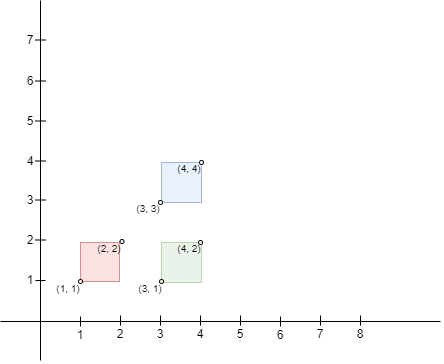
示例 3：

输入：bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]
输出：0
解释：不存在相交的矩形，因此，返回 0 。

 

提示：

  • n == bottomLeft.length == topRight.length
  • 2 <= n <= 103
  • bottomLeft[i].length == topRight[i].length == 2
  • 1 <= bottomLeft[i][0], bottomLeft[i][1] <= 107
  • 1 <= topRight[i][0], topRight[i][1] <= 107
  • bottomLeft[i][0] < topRight[i][0]
  • bottomLeft[i][1] < topRight[i][1]

解法

方法一：枚举

我们可以枚举两个矩形，其中矩形 $1$ 的左下角和右上角坐标分别为 $(x_1, y_1)$ 和 $(x_2, y_2)$，矩形 $2$ 的左下角和右上角坐标分别为 $(x_3, y_3)$ 和 $(x_4, y_4)$。

如果矩形 $1$ 和矩形 $2$ 有交集，那么交集的坐标分别为：

  • 左下角横坐标是两个矩形左下角横坐标的最大值，即 $\max(x_1, x_3)$；
  • 左下角纵坐标是两个矩形左下角纵坐标的最大值，即 $\max(y_1, y_3)$；
  • 右上角横坐标是两个矩形右上角横坐标的最小值，即 $\min(x_2, x_4)$；
  • 右上角纵坐标是两个矩形右上角纵坐标的最小值，即 $\min(y_2, y_4)$。

那么交集的宽和高分别为 $w = \min(x_2, x_4) - \max(x_1, x_3)$ 和 $h = \min(y_2, y_4) - \max(y_1, y_3)$。我们取两者的最小值作为边长，即 $e = \min(w, h)$，如果 $e &gt; 0$，那么我们就可以得到一个正方形，其面积为 $e^2$，我们取所有正方形的最大面积即可。

时间复杂度 $O(n^2)$，其中 $n$ 是矩形的数量。空间复杂度 $O(1)$。

Python3

class Solution:
    def largestSquareArea(
        self, bottomLeft: List[List[int]], topRight: List[List[int]]
    ) -> int:
        ans = 0
        for ((x1, y1), (x2, y2)), ((x3, y3), (x4, y4)) in combinations(
            zip(bottomLeft, topRight), 2
        ):
            w = min(x2, x4) - max(x1, x3)
            h = min(y2, y4) - max(y1, y3)
            e = min(w, h)
            if e > 0:
                ans = max(ans, e * e)
        return ans

Java

class Solution {
    public long largestSquareArea(int[][] bottomLeft, int[][] topRight) {
        long ans = 0;
        for (int i = 0; i < bottomLeft.length; ++i) {
            int x1 = bottomLeft[i][0], y1 = bottomLeft[i][1];
            int x2 = topRight[i][0], y2 = topRight[i][1];
            for (int j = i + 1; j < bottomLeft.length; ++j) {
                int x3 = bottomLeft[j][0], y3 = bottomLeft[j][1];
                int x4 = topRight[j][0], y4 = topRight[j][1];
                int w = Math.min(x2, x4) - Math.max(x1, x3);
                int h = Math.min(y2, y4) - Math.max(y1, y3);
                int e = Math.min(w, h);
                if (e > 0) {
                    ans = Math.max(ans, 1L * e * e);
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    long long largestSquareArea(vector<vector<int>>& bottomLeft, vector<vector<int>>& topRight) {
        long long ans = 0;
        for (int i = 0; i < bottomLeft.size(); ++i) {
            int x1 = bottomLeft[i][0], y1 = bottomLeft[i][1];
            int x2 = topRight[i][0], y2 = topRight[i][1];
            for (int j = i + 1; j < bottomLeft.size(); ++j) {
                int x3 = bottomLeft[j][0], y3 = bottomLeft[j][1];
                int x4 = topRight[j][0], y4 = topRight[j][1];
                int w = min(x2, x4) - max(x1, x3);
                int h = min(y2, y4) - max(y1, y3);
                int e = min(w, h);
                if (e > 0) {
                    ans = max(ans, 1LL * e * e);
                }
            }
        }
        return ans;
    }
};

Go

func largestSquareArea(bottomLeft [][]int, topRight [][]int) (ans int64) {
	for i, b1 := range bottomLeft {
		t1 := topRight[i]
		x1, y1 := b1[0], b1[1]
		x2, y2 := t1[0], t1[1]
		for j := i + 1; j < len(bottomLeft); j++ {
			x3, y3 := bottomLeft[j][0], bottomLeft[j][1]
			x4, y4 := topRight[j][0], topRight[j][1]
			w := min(x2, x4) - max(x1, x3)
			h := min(y2, y4) - max(y1, y3)
			e := min(w, h)
			if e > 0 {
				ans = max(ans, int64(e)*int64(e))
			}
		}
	}
	return
}

TypeScript

function largestSquareArea(bottomLeft: number[][], topRight: number[][]): number {
    let ans = 0;
    for (let i = 0; i < bottomLeft.length; ++i) {
        const [x1, y1] = bottomLeft[i];
        const [x2, y2] = topRight[i];
        for (let j = i + 1; j < bottomLeft.length; ++j) {
            const [x3, y3] = bottomLeft[j];
            const [x4, y4] = topRight[j];
            const w = Math.min(x2, x4) - Math.max(x1, x3);
            const h = Math.min(y2, y4) - Math.max(y1, y3);
            const e = Math.min(w, h);
            if (e > 0) {
                ans = Math.max(ans, e * e);
            }
        }
    }
    return ans;
}