Skip to content

Latest commit

 

History

History
227 lines (193 loc) · 8.09 KB

README.md

File metadata and controls

227 lines (193 loc) · 8.09 KB
Raw
comments difficulty edit_url rating source tags
true
困难
2709
第 381 场周赛 Q4
图
前缀和

3017. 按距离统计房屋对数目 II

English Version

题目描述

给你三个 正整数 n 、x 和 y 。

在城市中，存在编号从 1 到 n 的房屋，由 n 条街道相连。对所有 1 <= i < n ，都存在一条街道连接编号为 i 的房屋与编号为 i + 1 的房屋。另存在一条街道连接编号为 x 的房屋与编号为 y 的房屋。

对于每个 k（1 <= k <= n），你需要找出所有满足要求的 房屋对 [house1, house2] ，即从 house1 到 house2 需要经过的 最少 街道数为 k 。

返回一个下标从 1 开始且长度为 n 的数组 result ，其中 result[k] 表示所有满足要求的房屋对的数量，即从一个房屋到另一个房屋需要经过的 最少 街道数为 k 。

注意，x 与 y 可以 相等 。

 

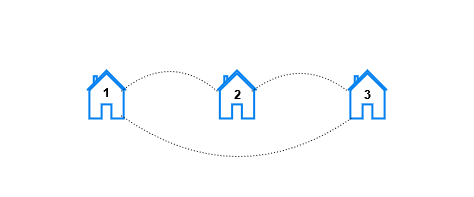
示例 1：

输入：n = 3, x = 1, y = 3
输出：[6,0,0]
解释：让我们检视每个房屋对
- 对于房屋对 (1, 2)，可以直接从房屋 1 到房屋 2。
- 对于房屋对 (2, 1)，可以直接从房屋 2 到房屋 1。
- 对于房屋对 (1, 3)，可以直接从房屋 1 到房屋 3。
- 对于房屋对 (3, 1)，可以直接从房屋 3 到房屋 1。
- 对于房屋对 (2, 3)，可以直接从房屋 2 到房屋 3。
- 对于房屋对 (3, 2)，可以直接从房屋 3 到房屋 2。

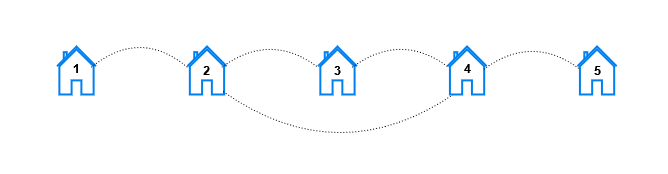
示例 2：

输入：n = 5, x = 2, y = 4
输出：[10,8,2,0,0]
解释：对于每个距离 k ，满足要求的房屋对如下：
- 对于 k == 1，满足要求的房屋对有 (1, 2), (2, 1), (2, 3), (3, 2), (2, 4), (4, 2), (3, 4), (4, 3), (4, 5), 以及 (5, 4)。
- 对于 k == 2，满足要求的房屋对有 (1, 3), (3, 1), (1, 4), (4, 1), (2, 5), (5, 2), (3, 5), 以及 (5, 3)。
- 对于 k == 3，满足要求的房屋对有 (1, 5)，以及 (5, 1) 。
- 对于 k == 4 和 k == 5，不存在满足要求的房屋对。

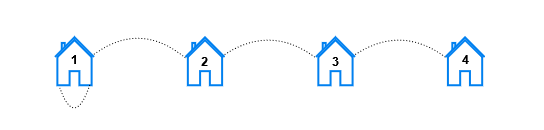
示例 3：

输入：n = 4, x = 1, y = 1
输出：[6,4,2,0]
解释：对于每个距离 k ，满足要求的房屋对如下：
- 对于 k == 1，满足要求的房屋对有 (1, 2), (2, 1), (2, 3), (3, 2), (3, 4), 以及 (4, 3)。
- 对于 k == 2，满足要求的房屋对有 (1, 3), (3, 1), (2, 4), 以及 (4, 2)。
- 对于 k == 3，满足要求的房屋对有 (1, 4), 以及 (4, 1)。
- 对于 k == 4，不存在满足要求的房屋对。

 

提示：

  • 2 <= n <= 105
  • 1 <= x, y <= n

解法

方法一

Python3

class Solution:
    def countOfPairs(self, n: int, x: int, y: int) -> List[int]:
        if abs(x - y) <= 1:
            return [2 * x for x in reversed(range(n))]
        cycle_len = abs(x - y) + 1
        n2 = n - cycle_len + 2
        res = [2 * x for x in reversed(range(n2))]
        while len(res) < n:
            res.append(0)
        res2 = [cycle_len * 2] * (cycle_len >> 1)
        if not cycle_len & 1:
            res2[-1] = cycle_len
        res2[0] -= 2
        for i in range(len(res2)):
            res[i] += res2[i]
        if x > y:
            x, y = y, x
        tail1 = x - 1
        tail2 = n - y
        for tail in (tail1, tail2):
            if not tail:
                continue
            i_mx = tail + (cycle_len >> 1)
            val_mx = 4 * min((cycle_len - 3) >> 1, tail)
            i_mx2 = i_mx - (1 - (cycle_len & 1))
            res3 = [val_mx] * i_mx
            res3[0] = 0
            res3[1] = 0
            if not cycle_len & 1:
                res3[-1] = 0
            for i, j in enumerate(range(4, val_mx, 4)):
                res3[i + 2] = j
                res3[i_mx2 - i - 1] = j
            for i in range(1, tail + 1):
                res3[i] += 2
            if not cycle_len & 1:
                mn = cycle_len >> 1
                for i in range(mn, mn + tail):
                    res3[i] += 2
            for i in range(len(res3)):
                res[i] += res3[i]
        return res

Java

class Solution {
    public long[] countOfPairs(int n, int x, int y) {
        --x;
        --y;
        if (x > y) {
        int temp = x;
        x = y;
        y = temp;
        }
        long[] diff = new long[n];
        for (int i = 0; i < n; ++i) {
        diff[0] += 1 + 1;
        ++diff[Math.min(Math.abs(i - x), Math.abs(i - y) + 1)];
        ++diff[Math.min(Math.abs(i - y), Math.abs(i - x) + 1)];
        --diff[Math.min(Math.abs(i - 0), Math.abs(i - y) + 1 + Math.abs(x - 0))];
        --diff[Math.min(Math.abs(i - (n - 1)),
                        Math.abs(i - x) + 1 + Math.abs(y - (n - 1)))];
        --diff[Math.max(x - i, 0) + Math.max(i - y, 0) + ((y - x) + 0) / 2];
        --diff[Math.max(x - i, 0) + Math.max(i - y, 0) + ((y - x) + 1) / 2];
        }
        for (int i = 0; i + 1 < n; ++i) {
        diff[i + 1] += diff[i];
        }
        return diff;
    }
}

C++

class Solution {
public:
  vector<long long> countOfPairs(int n, int x, int y) {
    --x, --y;
    if (x > y) {
      swap(x, y);
    }
    vector<long long> diff(n);
    for (int i = 0; i < n; ++i) {
      diff[0] += 1 + 1;
      ++diff[min(abs(i - x), abs(i - y) + 1)];
      ++diff[min(abs(i - y), abs(i - x) + 1)];
      --diff[min(abs(i - 0), abs(i - y) + 1 + abs(x - 0))];
      --diff[min(abs(i - (n - 1)), abs(i - x) + 1 + abs(y - (n - 1)))];
      --diff[max(x - i, 0) + max(i - y, 0) + ((y - x) + 0) / 2];
      --diff[max(x - i, 0) + max(i - y, 0) + ((y - x) + 1) / 2];
    }
    for (int i = 0; i + 1 < n; ++i) {
      diff[i + 1] += diff[i];
    }
    return diff;
  }
};

Go

func countOfPairs(n int, x int, y int) []int64 {
	if x > y {
		x, y = y, x
	}
	A := make([]int64, n)
	for i := 1; i <= n; i++ {
		A[0] += 2
		A[min(int64(i-1), int64(math.Abs(float64(i-y)))+int64(x))] -= 1
		A[min(int64(n-i), int64(math.Abs(float64(i-x)))+1+int64(n-y))] -= 1
		A[min(int64(math.Abs(float64(i-x))), int64(math.Abs(float64(y-i)))+1)] += 1
		A[min(int64(math.Abs(float64(i-x)))+1, int64(math.Abs(float64(y-i))))] += 1
		r := max(int64(x-i), 0) + max(int64(i-y), 0)
		A[r+int64((y-x+0)/2)] -= 1
		A[r+int64((y-x+1)/2)] -= 1
	}
	for i := 1; i < n; i++ {
		A[i] += A[i-1]
	}

	return A
}