Skip to content

Latest commit

 

History

History
214 lines (176 loc) · 6.16 KB

README.md

File metadata and controls

214 lines (176 loc) · 6.16 KB
Raw
comments difficulty edit_url rating source tags
true
中等
1625
第 345 场周赛 Q3
数组
动态规划
矩阵

2684. 矩阵中移动的最大次数

English Version

题目描述

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：

  • 从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。

返回你在矩阵中能够 移动 的 最大 次数。

 

示例 1：

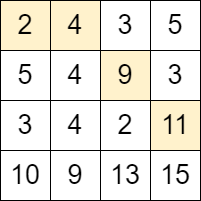
输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。

示例 2：


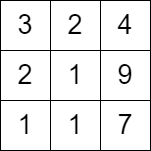
输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

 

提示：

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 1000
  • 4 <= m * n <= 105
  • 1 <= grid[i][j] <= 106

解法

方法一：BFS

我们定义一个队列 $q$，初始时将第一列的所有行坐标加入队列中。

接下来，我们从第一列开始，逐列进行遍历。对于每一列，我们将队列中的所有行坐标依次取出，然后对于每一个行坐标 $i$，我们得到其下一列的所有可能行坐标 $k$，并且满足 $grid[i][j] &lt; grid[k][j + 1]$，将这些行坐标加入到一个新的集合 $t$ 中。如果 $t$ 为空，说明我们无法继续移动，返回当前列数。否则，我们将 $t$ 赋值给 $q$，继续下一列的遍历。

最后，如果我们遍历完了所有列，说明我们可以移动到最后一列，返回 $n - 1$。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m)$。其中 $m$ 和 $n$ 分别是矩阵的行数和列数。

Python3

class Solution:
    def maxMoves(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        q = set(range(m))
        for j in range(n - 1):
            t = set()
            for i in q:
                for k in range(i - 1, i + 2):
                    if 0 <= k < m and grid[i][j] < grid[k][j + 1]:
                        t.add(k)
            if not t:
                return j
            q = t
        return n - 1

Java

class Solution {
    public int maxMoves(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        Set<Integer> q = IntStream.range(0, m).boxed().collect(Collectors.toSet());
        for (int j = 0; j < n - 1; ++j) {
            Set<Integer> t = new HashSet<>();
            for (int i : q) {
                for (int k = i - 1; k <= i + 1; ++k) {
                    if (k >= 0 && k < m && grid[i][j] < grid[k][j + 1]) {
                        t.add(k);
                    }
                }
            }
            if (t.isEmpty()) {
                return j;
            }
            q = t;
        }
        return n - 1;
    }
}

C++

class Solution {
public:
    int maxMoves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        unordered_set<int> q, t;
        for (int i = 0; i < m; ++i) {
            q.insert(i);
        }
        for (int j = 0; j < n - 1; ++j) {
            t.clear();
            for (int i : q) {
                for (int k = i - 1; k <= i + 1; ++k) {
                    if (k >= 0 && k < m && grid[i][j] < grid[k][j + 1]) {
                        t.insert(k);
                    }
                }
            }
            if (t.empty()) {
                return j;
            }
            q.swap(t);
        }
        return n - 1;
    }
};

Go

func maxMoves(grid [][]int) (ans int) {
	m, n := len(grid), len(grid[0])
	q := map[int]bool{}
	for i := range grid {
		q[i] = true
	}
	for j := 0; j < n-1; j++ {
		t := map[int]bool{}
		for i := range q {
			for k := i - 1; k <= i+1; k++ {
				if k >= 0 && k < m && grid[i][j] < grid[k][j+1] {
					t[k] = true
				}
			}
		}
		if len(t) == 0 {
			return j
		}
		q = t
	}
	return n - 1
}

TypeScript

function maxMoves(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    let q = new Set<number>(Array.from({ length: m }, (_, i) => i));
    for (let j = 0; j < n - 1; ++j) {
        const t = new Set<number>();
        for (const i of q) {
            for (let k = i - 1; k <= i + 1; ++k) {
                if (k >= 0 && k < m && grid[i][j] < grid[k][j + 1]) {
                    t.add(k);
                }
            }
        }
        if (t.size === 0) {
            return j;
        }
        q = t;
    }
    return n - 1;
}