comments

difficulty

edit_url

2361. Minimum Costs Using the Train Line 🔒

Description

A train line going through a city has two routes, the regular route and the express route. Both routes go through the same n + 1 stops labeled from 0 to n. Initially, you start on the regular route at stop 0.

You are given two 1-indexed integer arrays regular and express, both of length n. regular[i] describes the cost it takes to go from stop i - 1 to stop i using the regular route, and express[i] describes the cost it takes to go from stop i - 1 to stop i using the express route.

You are also given an integer expressCost which represents the cost to transfer from the regular route to the express route.

Note that:

There is no cost to transfer from the express route back to the regular route.
You pay expressCost every time you transfer from the regular route to the express route.
There is no extra cost to stay on the express route.

Return a 1-indexed array costs of length n, where costs[i] is the minimum cost to reach stop i from stop 0.

Note that a stop can be counted as reached from either route.

Example 1:

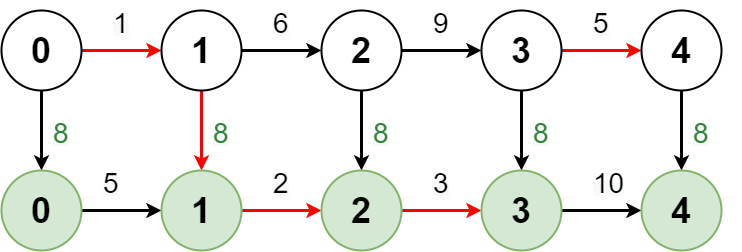
Input: regular = [1,6,9,5], express = [5,2,3,10], expressCost = 8
Output: [1,7,14,19]
Explanation: The diagram above shows how to reach stop 4 from stop 0 with minimum cost.
- Take the regular route from stop 0 to stop 1, costing 1.
- Take the express route from stop 1 to stop 2, costing 8 + 2 = 10.
- Take the express route from stop 2 to stop 3, costing 3.
- Take the regular route from stop 3 to stop 4, costing 5.
The total cost is 1 + 10 + 3 + 5 = 19.
Note that a different route could be taken to reach the other stops with minimum cost.

Example 2:

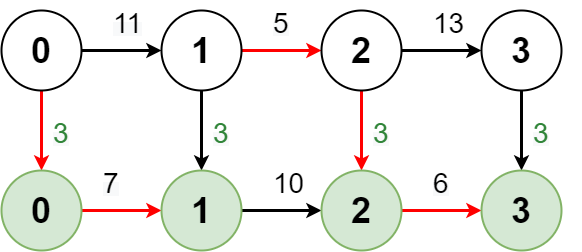
Input: regular = [11,5,13], express = [7,10,6], expressCost = 3
Output: [10,15,24]
Explanation: The diagram above shows how to reach stop 3 from stop 0 with minimum cost.
- Take the express route from stop 0 to stop 1, costing 3 + 7 = 10.
- Take the regular route from stop 1 to stop 2, costing 5.
- Take the express route from stop 2 to stop 3, costing 3 + 6 = 9.
The total cost is 10 + 5 + 9 = 24.
Note that the expressCost is paid again to transfer back to the express route.

Constraints:

n == regular.length == express.length
1 <= n <= 10⁵
1 <= regular[i], express[i], expressCost <= 10⁵

Solutions

Solution 1: Dynamic Programming

We define $f[i]$ as the minimum cost from station $0$ to station $i$ when arriving at station $i$ by the regular route, and $g[i]$ as the minimum cost from station $0$ to station $i$ when arriving at station $i$ by the express route. Initially, $f[0]=0, g[0]=\infty$.

Next, we consider how to transition the states of $f[i]$ and $g[i]$.

If we arrive at station $i$ by the regular route, we can either come from station $i-1$ by the regular route or switch from the express route at station $i-1$ to the regular route. Therefore, we can get the state transition equation:

$$ f[i]=\min{f[i-1]+a_i, g[i-1]+a_i} $$

where $a_i$ represents the cost of taking the regular route from station $i-1$ to station $i$.

If we arrive at station $i$ by the express route, we can either switch from the regular route at station $i-1$ to the express route or continue on the express route from station $i-1$. Therefore, we can get the state transition equation:

$$ g[i]=\min{f[i-1]+expressCost+b_i, g[i-1]+b_i} $$

where $b_i$ represents the cost of taking the express route from station $i-1$ to station $i$.

We denote the answer array as $cost$, where $cost[i]$ represents the minimum cost from station $0$ to station $i$. Since we can reach station $i$ from any route, we have $cost[i]=\min{f[i], g[i]}$.

Finally, we return $cost$.

The time complexity is $O(n)$ and the space complexity is $O(n)$, where $n$ is the number of stations.

Python3

class Solution:
    def minimumCosts(
        self, regular: List[int], express: List[int], expressCost: int
    ) -> List[int]:
        n = len(regular)
        f = [0] * (n + 1)
        g = [inf] * (n + 1)
        cost = [0] * n
        for i, (a, b) in enumerate(zip(regular, express), 1):
            f[i] = min(f[i - 1] + a, g[i - 1] + a)
            g[i] = min(f[i - 1] + expressCost + b, g[i - 1] + b)
            cost[i - 1] = min(f[i], g[i])
        return cost

Java

class Solution {
    public long[] minimumCosts(int[] regular, int[] express, int expressCost) {
        int n = regular.length;
        long[] f = new long[n + 1];
        long[] g = new long[n + 1];
        g[0] = 1 << 30;
        long[] cost = new long[n];
        for (int i = 1; i <= n; ++i) {
            int a = regular[i - 1];
            int b = express[i - 1];
            f[i] = Math.min(f[i - 1] + a, g[i - 1] + a);
            g[i] = Math.min(f[i - 1] + expressCost + b, g[i - 1] + b);
            cost[i - 1] = Math.min(f[i], g[i]);
        }
        return cost;
    }
}

C++

class Solution {
public:
    vector<long long> minimumCosts(vector<int>& regular, vector<int>& express, int expressCost) {
        int n = regular.size();
        long long f[n + 1];
        long long g[n + 1];
        f[0] = 0;
        g[0] = 1 << 30;
        vector<long long> cost(n);
        for (int i = 1; i <= n; ++i) {
            int a = regular[i - 1];
            int b = express[i - 1];
            f[i] = min(f[i - 1] + a, g[i - 1] + a);
            g[i] = min(f[i - 1] + expressCost + b, g[i - 1] + b);
            cost[i - 1] = min(f[i], g[i]);
        }
        return cost;
    }
};

Go

func minimumCosts(regular []int, express []int, expressCost int) []int64 {
	n := len(regular)
	f := make([]int, n+1)
	g := make([]int, n+1)
	g[0] = 1 << 30
	cost := make([]int64, n)
	for i := 1; i <= n; i++ {
		a, b := regular[i-1], express[i-1]
		f[i] = min(f[i-1]+a, g[i-1]+a)
		g[i] = min(f[i-1]+expressCost+b, g[i-1]+b)
		cost[i-1] = int64(min(f[i], g[i]))
	}
	return cost
}

TypeScript

function minimumCosts(regular: number[], express: number[], expressCost: number): number[] {
    const n = regular.length;
    const f: number[] = new Array(n + 1).fill(0);
    const g: number[] = new Array(n + 1).fill(0);
    g[0] = 1 << 30;
    const cost: number[] = new Array(n).fill(0);
    for (let i = 1; i <= n; ++i) {
        const [a, b] = [regular[i - 1], express[i - 1]];
        f[i] = Math.min(f[i - 1] + a, g[i - 1] + a);
        g[i] = Math.min(f[i - 1] + expressCost + b, g[i - 1] + b);
        cost[i - 1] = Math.min(f[i], g[i]);
    }
    return cost;
}

We notice that in the state transition equations of $f[i]$ and $g[i]$, we only need to use $f[i-1]$ and $g[i-1]$. Therefore, we can use two variables $f$ and $g$ to record the values of $f[i-1]$ and $g[i-1]$ respectively. This allows us to optimize the space complexity to $O(1)$.

Python3

class Solution:
    def minimumCosts(
        self, regular: List[int], express: List[int], expressCost: int
    ) -> List[int]:
        n = len(regular)
        f, g = 0, inf
        cost = [0] * n
        for i, (a, b) in enumerate(zip(regular, express), 1):
            ff = min(f + a, g + a)
            gg = min(f + expressCost + b, g + b)
            f, g = ff, gg
            cost[i - 1] = min(f, g)
        return cost

Java

class Solution {
    public long[] minimumCosts(int[] regular, int[] express, int expressCost) {
        int n = regular.length;
        long f = 0;
        long g = 1 << 30;
        long[] cost = new long[n];
        for (int i = 0; i < n; ++i) {
            int a = regular[i];
            int b = express[i];
            long ff = Math.min(f + a, g + a);
            long gg = Math.min(f + expressCost + b, g + b);
            f = ff;
            g = gg;
            cost[i] = Math.min(f, g);
        }
        return cost;
    }
}

C++

class Solution {
public:
    vector<long long> minimumCosts(vector<int>& regular, vector<int>& express, int expressCost) {
        int n = regular.size();
        long long f = 0;
        long long g = 1 << 30;
        vector<long long> cost(n);
        for (int i = 0; i < n; ++i) {
            int a = regular[i];
            int b = express[i];
            long long ff = min(f + a, g + a);
            long long gg = min(f + expressCost + b, g + b);
            f = ff;
            g = gg;
            cost[i] = min(f, g);
        }
        return cost;
    }
};

Go

func minimumCosts(regular []int, express []int, expressCost int) []int64 {
	f, g := 0, 1<<30
	cost := make([]int64, len(regular))
	for i, a := range regular {
		b := express[i]
		ff := min(f+a, g+a)
		gg := min(f+expressCost+b, g+b)
		f, g = ff, gg
		cost[i] = int64(min(f, g))
	}
	return cost
}

TypeScript

function minimumCosts(regular: number[], express: number[], expressCost: number): number[] {
    const n = regular.length;
    let f = 0;
    let g = 1 << 30;
    const cost: number[] = new Array(n).fill(0);
    for (let i = 0; i < n; ++i) {
        const [a, b] = [regular[i], express[i]];
        const ff = Math.min(f + a, g + a);
        const gg = Math.min(f + expressCost + b, g + b);
        [f, g] = [ff, gg];
        cost[i] = Math.min(f, g);
    }
    return cost;
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README_EN.md

README_EN.md

2361. Minimum Costs Using the Train Line 🔒

Description

Solutions

Solution 1: Dynamic Programming

Python3

Java

C++

Go

TypeScript

Python3

Java

C++

Go

TypeScript

Files

README_EN.md

Latest commit

History

README_EN.md

File metadata and controls

2361. Minimum Costs Using the Train Line 🔒

Description

Solutions

Solution 1: Dynamic Programming

Python3

Java

C++

Go

TypeScript

Python3

Java

C++

Go

TypeScript