Skip to content

Latest commit

 

History

History
310 lines (265 loc) · 9.35 KB

README.md

File metadata and controls

310 lines (265 loc) · 9.35 KB
Raw
comments difficulty edit_url rating source tags
true
困难
2391
第 299 场周赛 Q4
位运算
树
深度优先搜索
数组

2322. 从树中删除边的最小分数

English Version

题目描述

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点， 以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。

删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

  1. 分别获取三个组件 每个 组件中所有节点值的异或值。
  2. 最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。
  • 例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的 最小 分数。

 

示例 1：

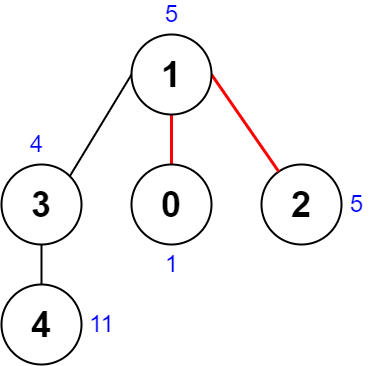
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出：9
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值，10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。

示例 2：

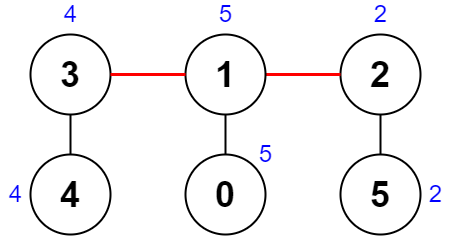
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出：0
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值，0 - 0 = 0 。
无法获得比 0 更小的分数 0 。

 

提示：

  • n == nums.length
  • 3 <= n <= 1000
  • 1 <= nums[i] <= 108
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • edges 表示一棵有效的树

解法

方法一：DFS + 子树异或和

枚举 $[0,n)$ 的每个点 $i$ 作为树的根节点，将根节点与某个子节点相连的边作为第一条被删除的边。这样我们就获得了两个连通块，我们记包含根节点 $i$ 的连通块为 $A$，不包含根节点 $i$ 的连通块为 $B$。

在 $A$ 中枚举第二条被删除的边。那么 $A$ 也会被划分成两个连通块 $C$ 和 $D$。

记每个连通块的异或和为 $S_i$，那么对于枚举的每一种情况，得到的分数为 $max(S_B, S_C, S_D)-min(S_B, S_C, S_D)$。求所有情况的最小值作为答案。

Python3

class Solution:
    def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
        def dfs(i, fa, x):
            res = nums[i]
            for j in g[i]:
                if j != fa and j != x:
                    res ^= dfs(j, i, x)
            return res

        def dfs2(i, fa, x):
            nonlocal s, s1, ans
            res = nums[i]
            for j in g[i]:
                if j != fa and j != x:
                    a = dfs2(j, i, x)
                    res ^= a
                    b = s1 ^ a
                    c = s ^ s1
                    t = max(a, b, c) - min(a, b, c)
                    ans = min(ans, t)
            return res

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)

        s = 0
        for v in nums:
            s ^= v
        n = len(nums)
        ans = inf
        for i in range(n):
            for j in g[i]:
                s1 = dfs(i, -1, j)
                dfs2(i, -1, j)
        return ans

Java

class Solution {
    private int s;
    private int s1;
    private int n;
    private int ans = Integer.MAX_VALUE;
    private int[] nums;
    private List<Integer>[] g;

    public int minimumScore(int[] nums, int[][] edges) {
        n = nums.length;
        g = new List[n];
        this.nums = nums;
        Arrays.setAll(g, k -> new ArrayList<>());
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        for (int v : nums) {
            s ^= v;
        }
        for (int i = 0; i < n; ++i) {
            for (int j : g[i]) {
                s1 = dfs(i, -1, j);
                dfs2(i, -1, j);
            }
        }
        return ans;
    }

    private int dfs(int i, int fa, int x) {
        int res = nums[i];
        for (int j : g[i]) {
            if (j != fa && j != x) {
                res ^= dfs(j, i, x);
            }
        }
        return res;
    }

    private int dfs2(int i, int fa, int x) {
        int res = nums[i];
        for (int j : g[i]) {
            if (j != fa && j != x) {
                int a = dfs2(j, i, x);
                res ^= a;
                int b = s1 ^ a;
                int c = s ^ s1;
                int t = Math.max(Math.max(a, b), c) - Math.min(Math.min(a, b), c);
                ans = Math.min(ans, t);
            }
        }
        return res;
    }
}

C++

class Solution {
public:
    vector<int> nums;
    int s;
    int s1;
    int n;
    int ans = INT_MAX;
    vector<vector<int>> g;

    int minimumScore(vector<int>& nums, vector<vector<int>>& edges) {
        n = nums.size();
        g.resize(n, vector<int>());
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        for (int& v : nums) s ^= v;
        this->nums = nums;
        for (int i = 0; i < n; ++i) {
            for (int j : g[i]) {
                s1 = dfs(i, -1, j);
                dfs2(i, -1, j);
            }
        }
        return ans;
    }

    int dfs(int i, int fa, int x) {
        int res = nums[i];
        for (int j : g[i])
            if (j != fa && j != x) res ^= dfs(j, i, x);
        return res;
    }

    int dfs2(int i, int fa, int x) {
        int res = nums[i];
        for (int j : g[i])
            if (j != fa && j != x) {
                int a = dfs2(j, i, x);
                res ^= a;
                int b = s1 ^ a;
                int c = s ^ s1;
                int t = max(max(a, b), c) - min(min(a, b), c);
                ans = min(ans, t);
            }
        return res;
    }
};

Go

func minimumScore(nums []int, edges [][]int) int {
	n := len(nums)
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	s := 0
	for _, v := range nums {
		s ^= v
	}
	s1 := 0
	ans := math.MaxInt32
	var dfs func(int, int, int) int
	var dfs2 func(int, int, int) int
	dfs = func(i, fa, x int) int {
		res := nums[i]
		for _, j := range g[i] {
			if j != fa && j != x {
				res ^= dfs(j, i, x)
			}
		}
		return res
	}
	dfs2 = func(i, fa, x int) int {
		res := nums[i]
		for _, j := range g[i] {
			if j != fa && j != x {
				a := dfs2(j, i, x)
				res ^= a
				b := s1 ^ a
				c := s ^ s1
				t := max(max(a, b), c) - min(min(a, b), c)
				ans = min(ans, t)
			}
		}
		return res
	}
	for i := 0; i < n; i++ {
		for _, j := range g[i] {
			s1 = dfs(i, -1, j)
			dfs2(i, -1, j)
		}
	}
	return ans
}