Skip to content

Latest commit

 

History

History
285 lines (240 loc) · 7.44 KB

README.md

File metadata and controls

285 lines (240 loc) · 7.44 KB
Raw
comments difficulty edit_url rating source tags
true
中等
1604
第 81 场双周赛 Q2
深度优先搜索
广度优先搜索
并查集
图

2316. 统计无向图中无法互相到达点对数

English Version

题目描述

给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。

请你返回 无法互相到达 的不同 点对数目 。

 

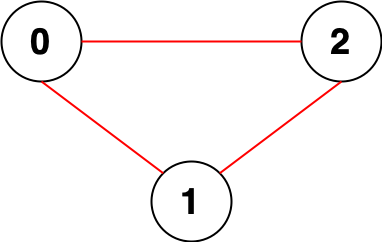
示例 1：

输入：n = 3, edges = [[0,1],[0,2],[1,2]]
输出：0
解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0 。

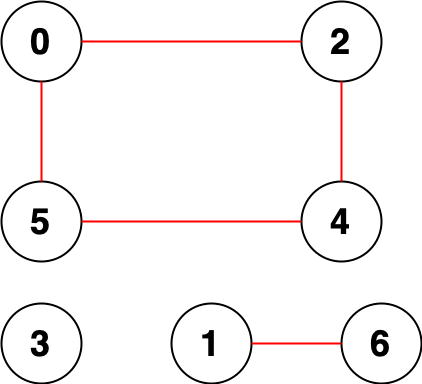
示例 2：

输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。

 

提示：

  • 1 <= n <= 105
  • 0 <= edges.length <= 2 * 105
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • 不会有重复边。

解法

方法一：DFS

对于无向图中的任意两个节点，如果它们之间存在一条路径，那么它们之间就是互相可达的。

因此，我们可以通过深度优先搜索的方式，找出每一个连通分量中的节点个数 $t$，然后将当前连通分量中的节点个数 $t$ 与之前所有连通分量中的节点个数 $s$ 相乘，即可得到当前连通分量中的不可达点对数目 $s \times t$，然后将 $t$ 加到 $s$ 中。继续搜索下一个连通分量，直到搜索完所有连通分量，即可得到答案。

时间复杂度 $O(n + m)$，空间复杂度 $O(n + m)$。其中 $n$ 和 $m$ 分别是节点数和边数。

Python3

class Solution:
    def countPairs(self, n: int, edges: List[List[int]]) -> int:
        def dfs(i: int) -> int:
            if vis[i]:
                return 0
            vis[i] = True
            return 1 + sum(dfs(j) for j in g[i])

        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        vis = [False] * n
        ans = s = 0
        for i in range(n):
            t = dfs(i)
            ans += s * t
            s += t
        return ans

Java

class Solution {
    private List<Integer>[] g;
    private boolean[] vis;

    public long countPairs(int n, int[][] edges) {
        g = new List[n];
        vis = new boolean[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        long ans = 0, s = 0;
        for (int i = 0; i < n; ++i) {
            int t = dfs(i);
            ans += s * t;
            s += t;
        }
        return ans;
    }

    private int dfs(int i) {
        if (vis[i]) {
            return 0;
        }
        vis[i] = true;
        int cnt = 1;
        for (int j : g[i]) {
            cnt += dfs(j);
        }
        return cnt;
    }
}

C++

class Solution {
public:
    long long countPairs(int n, vector<vector<int>>& edges) {
        vector<int> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        bool vis[n];
        memset(vis, 0, sizeof(vis));
        function<int(int)> dfs = [&](int i) {
            if (vis[i]) {
                return 0;
            }
            vis[i] = true;
            int cnt = 1;
            for (int j : g[i]) {
                cnt += dfs(j);
            }
            return cnt;
        };
        long long ans = 0, s = 0;
        for (int i = 0; i < n; ++i) {
            int t = dfs(i);
            ans += s * t;
            s += t;
        }
        return ans;
    }
};

Go

func countPairs(n int, edges [][]int) (ans int64) {
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	vis := make([]bool, n)
	var dfs func(int) int
	dfs = func(i int) int {
		if vis[i] {
			return 0
		}
		vis[i] = true
		cnt := 1
		for _, j := range g[i] {
			cnt += dfs(j)
		}
		return cnt
	}
	var s int64
	for i := 0; i < n; i++ {
		t := int64(dfs(i))
		ans += s * t
		s += t
	}
	return
}

TypeScript

function countPairs(n: number, edges: number[][]): number {
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    const vis: boolean[] = Array(n).fill(false);
    const dfs = (i: number): number => {
        if (vis[i]) {
            return 0;
        }
        vis[i] = true;
        let cnt = 1;
        for (const j of g[i]) {
            cnt += dfs(j);
        }
        return cnt;
    };
    let [ans, s] = [0, 0];
    for (let i = 0; i < n; ++i) {
        const t = dfs(i);
        ans += s * t;
        s += t;
    }
    return ans;
}

Rust

impl Solution {
    pub fn count_pairs(n: i32, edges: Vec<Vec<i32>>) -> i64 {
        let n = n as usize;
        let mut g = vec![vec![]; n];
        let mut vis = vec![false; n];
        for e in edges {
            let u = e[0] as usize;
            let v = e[1] as usize;
            g[u].push(v);
            g[v].push(u);
        }

        fn dfs(g: &Vec<Vec<usize>>, vis: &mut Vec<bool>, u: usize) -> i64 {
            if vis[u] {
                return 0;
            }
            vis[u] = true;
            let mut cnt = 1;
            for &v in &g[u] {
                cnt += dfs(g, vis, v);
            }
            cnt
        }

        let mut ans = 0;
        let mut s = 0;
        for u in 0..n {
            let t = dfs(&g, &mut vis, u);
            ans += t * s;
            s += t;
        }
        ans
    }
}