README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/2300-2399/2304.Minimum%20Path%20Cost%20in%20a%20Grid/README_EN.md	1658	Weekly Contest 297 Q2	Array Dynamic Programming Matrix

2304. Minimum Path Cost in a Grid

中文文档

Description

You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1). Note that it is not possible to move from cells in the last row.

Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.

The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.

 

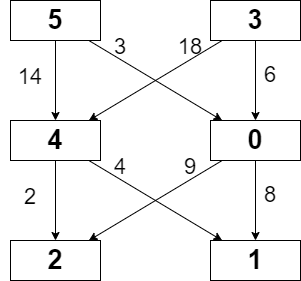
Example 1:

Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
Output: 17
Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.

Example 2:

Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
Output: 6
Explanation: The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• grid consists of distinct integers from 0 to m * n - 1.
• moveCost.length == m * n
• moveCost[i].length == n
• 1 <= moveCost[i][j] <= 100

Solutions

Solution 1: Dynamic Programming

We define $f[i][j]$ to represent the minimum path cost from the first row to the $i$th row and $j$th column. Since we can only move from a column in the previous row to a column in the current row, the value of $f[i][j]$ can be transferred from $f[i - 1][k]$, where the range of $k$ is $[0, n - 1]$. Therefore, the state transition equation is:

$$ f[i][j] = \min_{0 \leq k < n} {f[i - 1][k] + \text{moveCost}[grid[i - 1][k]][j] + grid[i][j]} $$

where $\text{moveCost}[grid[i - 1][k]][j]$ represents the cost of moving from the $k$th column of the $i - 1$th row to the $j$th column of the $i$th row.

The final answer is $\min_{0 \leq j &lt; n} {f[m - 1][j]}$.

Since each transition only needs the state of the previous row, we can use a rolling array to optimize the space complexity to $O(n)$.

The time complexity is $O(m \times n^2)$, and the space complexity is $O(n)$. Here, $m$ and $n$ are the number of rows and columns of the grid, respectively.

Python3

class Solution:
    def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        f = grid[0]
        for i in range(1, m):
            g = [inf] * n
            for j in range(n):
                for k in range(n):
                    g[j] = min(g[j], f[k] + moveCost[grid[i - 1][k]][j] + grid[i][j])
            f = g
        return min(f)

Java

class Solution {
    public int minPathCost(int[][] grid, int[][] moveCost) {
        int m = grid.length, n = grid[0].length;
        int[] f = grid[0];
        final int inf = 1 << 30;
        for (int i = 1; i < m; ++i) {
            int[] g = new int[n];
            Arrays.fill(g, inf);
            for (int j = 0; j < n; ++j) {
                for (int k = 0; k < n; ++k) {
                    g[j] = Math.min(g[j], f[k] + moveCost[grid[i - 1][k]][j] + grid[i][j]);
                }
            }
            f = g;
        }

        // return Arrays.stream(f).min().getAsInt();
        int ans = inf;
        for (int v : f) {
            ans = Math.min(ans, v);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
        int m = grid.size(), n = grid[0].size();
        const int inf = 1 << 30;
        vector<int> f = grid[0];
        for (int i = 1; i < m; ++i) {
            vector<int> g(n, inf);
            for (int j = 0; j < n; ++j) {
                for (int k = 0; k < n; ++k) {
                    g[j] = min(g[j], f[k] + moveCost[grid[i - 1][k]][j] + grid[i][j]);
                }
            }
            f = move(g);
        }
        return *min_element(f.begin(), f.end());
    }
};

Go

func minPathCost(grid [][]int, moveCost [][]int) int {
	m, n := len(grid), len(grid[0])
	f := grid[0]
	for i := 1; i < m; i++ {
		g := make([]int, n)
		for j := 0; j < n; j++ {
			g[j] = 1 << 30
			for k := 0; k < n; k++ {
				g[j] = min(g[j], f[k]+moveCost[grid[i-1][k]][j]+grid[i][j])
			}
		}
		f = g
	}
	return slices.Min(f)
}

TypeScript

function minPathCost(grid: number[][], moveCost: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const f = grid[0];
    for (let i = 1; i < m; ++i) {
        const g: number[] = Array(n).fill(Infinity);
        for (let j = 0; j < n; ++j) {
            for (let k = 0; k < n; ++k) {
                g[j] = Math.min(g[j], f[k] + moveCost[grid[i - 1][k]][j] + grid[i][j]);
            }
        }
        f.splice(0, n, ...g);
    }
    return Math.min(...f);
}

Rust

impl Solution {
    pub fn min_path_cost(grid: Vec<Vec<i32>>, move_cost: Vec<Vec<i32>>) -> i32 {
        let m = grid.len();
        let n = grid[0].len();
        let mut f = grid[0].clone();

        for i in 1..m {
            let mut g: Vec<i32> = vec![i32::MAX; n];
            for j in 0..n {
                for k in 0..n {
                    g[j] = g[j].min(f[k] + move_cost[grid[i - 1][k] as usize][j] + grid[i][j]);
                }
            }
            f.copy_from_slice(&g);
        }

        f.iter().cloned().min().unwrap_or(0)
    }
}