README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Hard	https://github.com/doocs/leetcode/edit/main/solution/2200-2299/2267.Check%20if%20There%20Is%20a%20Valid%20Parentheses%20String%20Path/README_EN.md	2084	Weekly Contest 292 Q4	Array Dynamic Programming Matrix

2267. Check if There Is a Valid Parentheses String Path

中文文档

Description

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:

• It is ().
• It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
• It can be written as (A), where A is a valid parentheses string.

You are given an m x n matrix of parentheses grid. A valid parentheses string path in the grid is a path satisfying all of the following conditions:

• The path starts from the upper left cell (0, 0).
• The path ends at the bottom-right cell (m - 1, n - 1).
• The path only ever moves down or right.
• The resulting parentheses string formed by the path is valid.

Return true if there exists a valid parentheses string path in the grid. Otherwise, return false.

 

Example 1:

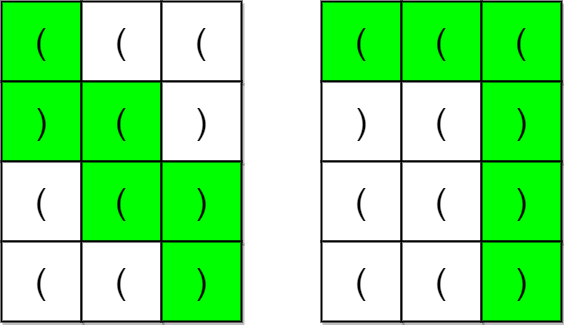
Input: grid = [["(","(","("],[")","(",")"],["(","(",")"],["(","(",")"]]
Output: true
Explanation: The above diagram shows two possible paths that form valid parentheses strings.
The first path shown results in the valid parentheses string "()(())".
The second path shown results in the valid parentheses string "((()))".
Note that there may be other valid parentheses string paths.

Example 2:

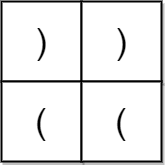
Input: grid = [[")",")"],["(","("]]
Output: false
Explanation: The two possible paths form the parentheses strings "))(" and ")((". Since neither of them are valid parentheses strings, we return false.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• grid[i][j] is either '(' or ')'.

Solutions

Solution 1

Python3

class Solution:
    def hasValidPath(self, grid: List[List[str]]) -> bool:
        @cache
        def dfs(i, j, t):
            if grid[i][j] == '(':
                t += 1
            else:
                t -= 1
            if t < 0:
                return False
            if i == m - 1 and j == n - 1:
                return t == 0
            for x, y in [(i + 1, j), (i, j + 1)]:
                if x < m and y < n and dfs(x, y, t):
                    return True
            return False

        m, n = len(grid), len(grid[0])
        return dfs(0, 0, 0)

Java

class Solution {
    private boolean[][][] vis;
    private char[][] grid;
    private int m;
    private int n;

    public boolean hasValidPath(char[][] grid) {
        m = grid.length;
        n = grid[0].length;
        this.grid = grid;
        vis = new boolean[m][n][m + n];
        return dfs(0, 0, 0);
    }

    private boolean dfs(int i, int j, int t) {
        if (vis[i][j][t]) {
            return false;
        }
        vis[i][j][t] = true;
        t += grid[i][j] == '(' ? 1 : -1;
        if (t < 0) {
            return false;
        }
        if (i == m - 1 && j == n - 1) {
            return t == 0;
        }
        int[] dirs = {0, 1, 0};
        for (int k = 0; k < 2; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < m && y < n && dfs(x, y, t)) {
                return true;
            }
        }
        return false;
    }
}

C++

bool vis[100][100][200];
int dirs[3] = {1, 0, 1};

class Solution {
public:
    bool hasValidPath(vector<vector<char>>& grid) {
        memset(vis, 0, sizeof(vis));
        return dfs(0, 0, 0, grid);
    }

    bool dfs(int i, int j, int t, vector<vector<char>>& grid) {
        if (vis[i][j][t]) return false;
        vis[i][j][t] = true;
        t += grid[i][j] == '(' ? 1 : -1;
        if (t < 0) return false;
        int m = grid.size(), n = grid[0].size();
        if (i == m - 1 && j == n - 1) return t == 0;
        for (int k = 0; k < 2; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < m && y < n && dfs(x, y, t, grid)) return true;
        }
        return false;
    }
};

Go

func hasValidPath(grid [][]byte) bool {
	m, n := len(grid), len(grid[0])
	vis := make([][][]bool, m)
	for i := range vis {
		vis[i] = make([][]bool, n)
		for j := range vis[i] {
			vis[i][j] = make([]bool, m+n)
		}
	}
	var dfs func(int, int, int) bool
	dfs = func(i, j, t int) bool {
		if vis[i][j][t] {
			return false
		}
		vis[i][j][t] = true
		if grid[i][j] == '(' {
			t += 1
		} else {
			t -= 1
		}
		if t < 0 {
			return false
		}
		if i == m-1 && j == n-1 {
			return t == 0
		}
		dirs := []int{1, 0, 1}
		for k := 0; k < 2; k++ {
			x, y := i+dirs[k], j+dirs[k+1]
			if x < m && y < n && dfs(x, y, t) {
				return true
			}
		}
		return false
	}
	return dfs(0, 0, 0)
}