| comments | difficulty | edit_url | tags | ||
|---|---|---|---|---|---|
true |
中等 |
|
给你一个整数 n,代表你拥有牌的数量。一个 纸牌屋 满足以下条件:
- 一个 纸牌屋 由一行或多行 三角形 和水平纸牌组成。
- 三角形 是由两张卡片相互靠在一起形成的。
- 一张卡片必须水平放置在一行中 所有相邻 的三角形之间。
- 比第一行高的任何三角形都必须放在前一行的水平牌上。
- 每个三角形都被放置在行中 最左边 的可用位置。
返回使用所有 n 张卡片可以构建的不同纸牌屋的数量。如果存在一行两个纸牌屋包含不同数量的纸牌,那么两个纸牌屋被认为是不同的。
示例 1:
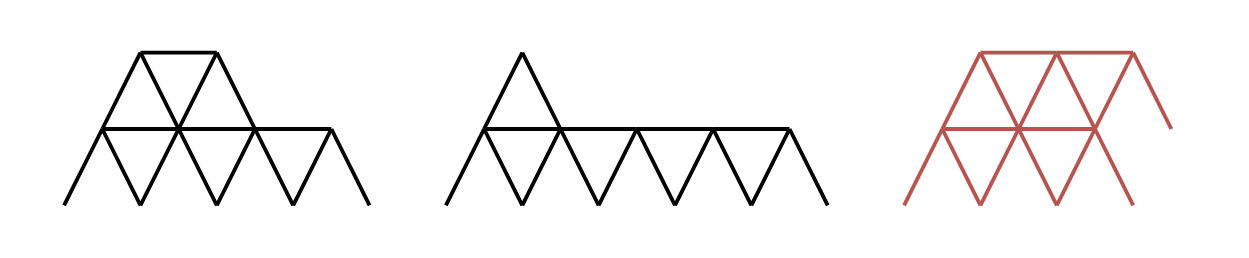
输入: n = 16 输出: 2 解释: 有两种有效的纸牌屋摆法。 图中的第三个纸牌屋无效,因为第一行最右边的三角形没有放在水平纸牌的顶部。
Example 2:
输入: n = 2 输出: 1 解释: 这是唯一可行的纸牌屋。
Example 3:
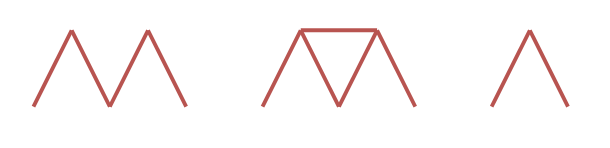
输入: n = 4 输出: 0 解释: 图中的三种纸牌都是无效的。 第一个纸牌屋需要在两个三角形之间放置一张水平纸牌。 第二个纸牌屋使用 5 张纸牌。 第三个纸牌屋使用 2 张纸牌。
提示:
1 <= n <= 500
我们注意到,每一层的卡片数量为
我们设计一个函数
函数
- 如果
$3 \times k + 2 \gt n$ ,那么当前层无法放置任何卡片,返回$0$ ; - 如果
$3 \times k + 2 = n$ ,那么当前层可以放置卡片,放置完毕后,整个纸牌屋已经构建完毕,返回$1$ ; - 否则,我们可以选择不放置卡片,或者放置卡片。如果选择不放置卡片,那么剩余卡片数量不变,层数增加
$1$ ,即$dfs(n, k + 1)$ ;如果选择放置卡片,那么剩余卡片数量减少$3 \times k + 2$ ,层数增加$1$ ,即$dfs(n - (3 \times k + 2), k + 1)$ 。两者相加即为答案。
过程中,我们可以使用记忆化搜索,避免重复计算。
时间复杂度
class Solution:
def houseOfCards(self, n: int) -> int:
@cache
def dfs(n: int, k: int) -> int:
x = 3 * k + 2
if x > n:
return 0
if x == n:
return 1
return dfs(n - x, k + 1) + dfs(n, k + 1)
return dfs(n, 0)class Solution {
private Integer[][] f;
public int houseOfCards(int n) {
f = new Integer[n + 1][n / 3];
return dfs(n, 0);
}
private int dfs(int n, int k) {
int x = 3 * k + 2;
if (x > n) {
return 0;
}
if (x == n) {
return 1;
}
if (f[n][k] != null) {
return f[n][k];
}
return f[n][k] = dfs(n - x, k + 1) + dfs(n, k + 1);
}
}class Solution {
public:
int houseOfCards(int n) {
int f[n + 1][n / 3 + 1];
memset(f, -1, sizeof(f));
function<int(int, int)> dfs = [&](int n, int k) -> int {
int x = 3 * k + 2;
if (x > n) {
return 0;
}
if (x == n) {
return 1;
}
if (f[n][k] != -1) {
return f[n][k];
}
return f[n][k] = dfs(n - x, k + 1) + dfs(n, k + 1);
};
return dfs(n, 0);
}
};func houseOfCards(n int) int {
f := make([][]int, n+1)
for i := range f {
f[i] = make([]int, n/3+1)
for j := range f[i] {
f[i][j] = -1
}
}
var dfs func(n, k int) int
dfs = func(n, k int) int {
x := 3*k + 2
if x > n {
return 0
}
if x == n {
return 1
}
if f[n][k] == -1 {
f[n][k] = dfs(n-x, k+1) + dfs(n, k+1)
}
return f[n][k]
}
return dfs(n, 0)
}function houseOfCards(n: number): number {
const f: number[][] = Array(n + 1)
.fill(0)
.map(() => Array(Math.floor(n / 3) + 1).fill(-1));
const dfs = (n: number, k: number): number => {
const x = k * 3 + 2;
if (x > n) {
return 0;
}
if (x === n) {
return 1;
}
if (f[n][k] === -1) {
f[n][k] = dfs(n - x, k + 1) + dfs(n, k + 1);
}
return f[n][k];
};
return dfs(n, 0);
}