Skip to content

Latest commit

 

History

History
231 lines (190 loc) · 6.69 KB

README_EN.md

File metadata and controls

231 lines (190 loc) · 6.69 KB
Raw
comments difficulty edit_url tags
true
Medium
Array
Ordered Set
Prefix Sum

2021. Brightest Position on Street 🔒

中文文档

Description

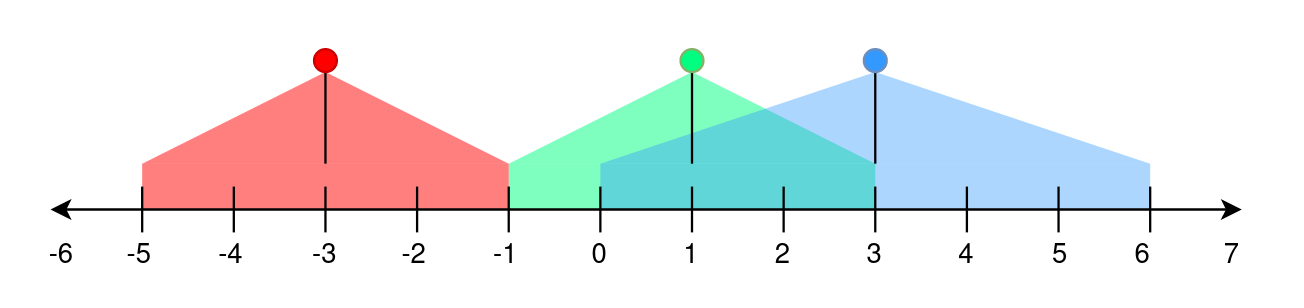
A perfectly straight street is represented by a number line. The street has street lamp(s) on it and is represented by a 2D integer array lights. Each lights[i] = [positioni, rangei] indicates that there is a street lamp at position positioni that lights up the area from [positioni - rangei, positioni + rangei] (inclusive).

The brightness of a position p is defined as the number of street lamp that light up the position p.

Given lights, return the brightest position on the street. If there are multiple brightest positions, return the smallest one.

 

Example 1:

Input: lights = [[-3,2],[1,2],[3,3]]
Output: -1
Explanation:
The first street lamp lights up the area from [(-3) - 2, (-3) + 2] = [-5, -1].
The second street lamp lights up the area from [1 - 2, 1 + 2] = [-1, 3].
The third street lamp lights up the area from [3 - 3, 3 + 3] = [0, 6].

Position -1 has a brightness of 2, illuminated by the first and second street light.
Positions 0, 1, 2, and 3 have a brightness of 2, illuminated by the second and third street light.
Out of all these positions, -1 is the smallest, so return it.

Example 2:

Input: lights = [[1,0],[0,1]]
Output: 1
Explanation:
The first street lamp lights up the area from [1 - 0, 1 + 0] = [1, 1].
The second street lamp lights up the area from [0 - 1, 0 + 1] = [-1, 1].

Position 1 has a brightness of 2, illuminated by the first and second street light.
Return 1 because it is the brightest position on the street.

Example 3:

Input: lights = [[1,2]]
Output: -1
Explanation:
The first street lamp lights up the area from [1 - 2, 1 + 2] = [-1, 3].

Positions -1, 0, 1, 2, and 3 have a brightness of 1, illuminated by the first street light.
Out of all these positions, -1 is the smallest, so return it.

 

Constraints:

  • 1 <= lights.length <= 105
  • lights[i].length == 2
  • -108 <= positioni <= 108
  • 0 <= rangei <= 108

Solutions

Solution 1: Difference Array + Hash Table + Sorting

We can consider the range illuminated by each street light as an interval, with the left endpoint $l = position_i - range_i$ and the right endpoint $r = position_i + range_i$. We can use the idea of a difference array. For each interval $[l, r]$, we add $1$ to the value at position $l$ and subtract $1$ from the value at position $r + 1$. We use a hash table to maintain the change value at each position.

Then we traverse each position in ascending order, calculate the brightness $s$ at the current position. If the previous maximum brightness $mx &lt; s$, then update the maximum brightness $mx = s$ and record the current position $ans = i$.

Finally, return $ans$.

The time complexity is $O(n \times \log n)$, and the space complexity is $O(n)$. Here, $n$ is the length of lights.

Python3

class Solution:
    def brightestPosition(self, lights: List[List[int]]) -> int:
        d = defaultdict(int)
        for i, j in lights:
            l, r = i - j, i + j
            d[l] += 1
            d[r + 1] -= 1
        ans = s = mx = 0
        for k in sorted(d):
            s += d[k]
            if mx < s:
                mx = s
                ans = k
        return ans

Java

class Solution {
    public int brightestPosition(int[][] lights) {
        TreeMap<Integer, Integer> d = new TreeMap<>();
        for (var x : lights) {
            int l = x[0] - x[1], r = x[0] + x[1];
            d.merge(l, 1, Integer::sum);
            d.merge(r + 1, -1, Integer::sum);
        }
        int ans = 0, s = 0, mx = 0;
        for (var x : d.entrySet()) {
            int v = x.getValue();
            s += v;
            if (mx < s) {
                mx = s;
                ans = x.getKey();
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int brightestPosition(vector<vector<int>>& lights) {
        map<int, int> d;
        for (auto& x : lights) {
            int l = x[0] - x[1], r = x[0] + x[1];
            ++d[l];
            --d[r + 1];
        }
        int ans = 0, s = 0, mx = 0;
        for (auto& [i, v] : d) {
            s += v;
            if (mx < s) {
                mx = s;
                ans = i;
            }
        }
        return ans;
    }
};

Go

func brightestPosition(lights [][]int) (ans int) {
	d := map[int]int{}
	for _, x := range lights {
		l, r := x[0]-x[1], x[0]+x[1]
		d[l]++
		d[r+1]--
	}
	keys := make([]int, 0, len(d))
	for i := range d {
		keys = append(keys, i)
	}
	sort.Ints(keys)
	mx, s := 0, 0
	for _, i := range keys {
		s += d[i]
		if mx < s {
			mx = s
			ans = i
		}
	}
	return
}

JavaScript

/**
 * @param {number[][]} lights
 * @return {number}
 */
var brightestPosition = function (lights) {
    const d = new Map();
    for (const [i, j] of lights) {
        const l = i - j;
        const r = i + j;
        d.set(l, (d.get(l) ?? 0) + 1);
        d.set(r + 1, (d.get(r + 1) ?? 0) - 1);
    }
    const keys = [];
    for (const k of d.keys()) {
        keys.push(k);
    }
    keys.sort((a, b) => a - b);
    let ans = 0;
    let s = 0;
    let mx = 0;
    for (const i of keys) {
        s += d.get(i);
        if (mx < s) {
            mx = s;
            ans = i;
        }
    }
    return ans;
};