comments

difficulty

edit_url

rating

source

2003. 每棵子树内缺失的最小基因值

题目描述

有一棵根节点为 0 的 家族树 ，总共包含 n 个节点，节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ，其中 parents[i] 是节点 i 的父节点。由于节点 0 是根，所以 parents[0] == -1 。

总共有 10⁵ 个基因值，每个基因值都用 闭区间 [1, 10⁵] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ，其中 nums[i] 是节点 i 的基因值，且基因值 互不相同 。

请你返回一个数组 ans ，长度为 n ，其中 ans[i] 是以节点 i 为根的子树内缺失的最小基因值。

节点 x 为根的子树包含节点 x 和它所有的后代节点。

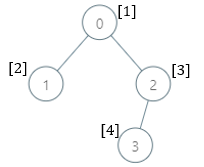
示例 1：

输入：parents = [-1,0,0,2], nums = [1,2,3,4]
输出：[5,1,1,1]
解释：每个子树答案计算结果如下：
- 0：子树包含节点 [0,1,2,3] ，基因值分别为 [1,2,3,4] 。5 是缺失的最小基因值。
- 1：子树只包含节点 1 ，基因值为 2 。1 是缺失的最小基因值。
- 2：子树包含节点 [2,3] ，基因值分别为 [3,4] 。1 是缺失的最小基因值。
- 3：子树只包含节点 3 ，基因值为 4 。1是缺失的最小基因值。

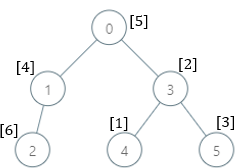
示例 2：

输入：parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
输出：[7,1,1,4,2,1]
解释：每个子树答案计算结果如下：
- 0：子树内包含节点 [0,1,2,3,4,5] ，基因值分别为 [5,4,6,2,1,3] 。7 是缺失的最小基因值。
- 1：子树内包含节点 [1,2] ，基因值分别为 [4,6] 。 1 是缺失的最小基因值。
- 2：子树内只包含节点 2 ，基因值为 6 。1 是缺失的最小基因值。
- 3：子树内包含节点 [3,4,5] ，基因值分别为 [2,1,3] 。4 是缺失的最小基因值。
- 4：子树内只包含节点 4 ，基因值为 1 。2 是缺失的最小基因值。
- 5：子树内只包含节点 5 ，基因值为 3 。1 是缺失的最小基因值。

示例 3：

输入：parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
输出：[1,1,1,1,1,1,1]
解释：所有子树都缺失基因值 1 。

提示：

n == parents.length == nums.length
2 <= n <= 10⁵
对于 i != 0 ，满足 0 <= parents[i] <= n - 1
parents[0] == -1
parents 表示一棵合法的树。
1 <= nums[i] <= 10⁵
nums[i] 互不相同。

解法

方法一：DFS

我们注意到，每个节点的基因值互不相同，因此，我们只需要找到基因值为 $1$ 的节点 $idx$，那么除了从节点 $idx$ 到根节点 $0$ 的每个节点，其它节点的答案都是 $1$。

因此，我们初始化答案数组 $ans$ 为 $[1,1,...,1]$，然后我们的重点就在于求出节点 $idx$ 到根节点 $0$ 的路径上的每个节点的答案。

我们可以从节点 $idx$ 开始，通过深度优先搜索的方式，标记以 $idx$ 作为根节点的子树中出现过的基因值，记录在数组 $has$ 中。搜索过程中，我们用一个数组 $vis$ 标记已经访问过的节点，防止重复访问。

接下来，我们从 $i=2$ 开始，不断向后寻找第一个没有出现过的基因值，即为节点 $idx$ 的答案。这里 $i$ 是严格递增的，因为基因值互不相同，所以我们一定能在 $[1,..n+1]$ 中找到一个没有出现过的基因值。

然后，我们更新节点 $idx$ 的答案，即 $ans[idx]=i$，并将 $idx$ 更新为其父节点，继续上述过程，直到 $idx=-1$，即到达了根节点 $0$。

最后，我们返回答案数组 $ans$ 即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是节点的数量。

Python3

class Solution:
    def smallestMissingValueSubtree(
        self, parents: List[int], nums: List[int]
    ) -> List[int]:
        def dfs(i: int):
            if vis[i]:
                return
            vis[i] = True
            if nums[i] < len(has):
                has[nums[i]] = True
            for j in g[i]:
                dfs(j)

        n = len(nums)
        ans = [1] * n
        g = [[] for _ in range(n)]
        idx = -1
        for i, p in enumerate(parents):
            if i:
                g[p].append(i)
            if nums[i] == 1:
                idx = i
        if idx == -1:
            return ans
        vis = [False] * n
        has = [False] * (n + 2)
        i = 2
        while idx != -1:
            dfs(idx)
            while has[i]:
                i += 1
            ans[idx] = i
            idx = parents[idx]
        return ans

Java

class Solution {
    private List<Integer>[] g;
    private boolean[] vis;
    private boolean[] has;
    private int[] nums;

    public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
        int n = nums.length;
        this.nums = nums;
        g = new List[n];
        vis = new boolean[n];
        has = new boolean[n + 2];
        Arrays.setAll(g, i -> new ArrayList<>());
        int idx = -1;
        for (int i = 0; i < n; ++i) {
            if (i > 0) {
                g[parents[i]].add(i);
            }
            if (nums[i] == 1) {
                idx = i;
            }
        }
        int[] ans = new int[n];
        Arrays.fill(ans, 1);
        if (idx == -1) {
            return ans;
        }
        for (int i = 2; idx != -1; idx = parents[idx]) {
            dfs(idx);
            while (has[i]) {
                ++i;
            }
            ans[idx] = i;
        }
        return ans;
    }

    private void dfs(int i) {
        if (vis[i]) {
            return;
        }
        vis[i] = true;
        if (nums[i] < has.length) {
            has[nums[i]] = true;
        }
        for (int j : g[i]) {
            dfs(j);
        }
    }
}

C++

class Solution {
public:
    vector<int> smallestMissingValueSubtree(vector<int>& parents, vector<int>& nums) {
        int n = nums.size();
        vector<int> g[n];
        bool vis[n];
        bool has[n + 2];
        memset(vis, false, sizeof(vis));
        memset(has, false, sizeof(has));
        int idx = -1;
        for (int i = 0; i < n; ++i) {
            if (i) {
                g[parents[i]].push_back(i);
            }
            if (nums[i] == 1) {
                idx = i;
            }
        }
        vector<int> ans(n, 1);
        if (idx == -1) {
            return ans;
        }
        function<void(int)> dfs = [&](int i) {
            if (vis[i]) {
                return;
            }
            vis[i] = true;
            if (nums[i] < n + 2) {
                has[nums[i]] = true;
            }
            for (int j : g[i]) {
                dfs(j);
            }
        };
        for (int i = 2; ~idx; idx = parents[idx]) {
            dfs(idx);
            while (has[i]) {
                ++i;
            }
            ans[idx] = i;
        }
        return ans;
    }
};

Go

func smallestMissingValueSubtree(parents []int, nums []int) []int {
	n := len(nums)
	g := make([][]int, n)
	vis := make([]bool, n)
	has := make([]bool, n+2)
	idx := -1
	ans := make([]int, n)
	for i, p := range parents {
		if i > 0 {
			g[p] = append(g[p], i)
		}
		if nums[i] == 1 {
			idx = i
		}
		ans[i] = 1
	}
	if idx < 0 {
		return ans
	}
	var dfs func(int)
	dfs = func(i int) {
		if vis[i] {
			return
		}
		vis[i] = true
		if nums[i] < len(has) {
			has[nums[i]] = true
		}
		for _, j := range g[i] {
			dfs(j)
		}
	}
	for i := 2; idx != -1; idx = parents[idx] {
		dfs(idx)
		for has[i] {
			i++
		}
		ans[idx] = i
	}
	return ans
}

TypeScript

function smallestMissingValueSubtree(parents: number[], nums: number[]): number[] {
    const n = nums.length;
    const g: number[][] = Array.from({ length: n }, () => []);
    const vis: boolean[] = Array(n).fill(false);
    const has: boolean[] = Array(n + 2).fill(false);
    const ans: number[] = Array(n).fill(1);
    let idx = -1;
    for (let i = 0; i < n; ++i) {
        if (i) {
            g[parents[i]].push(i);
        }
        if (nums[i] === 1) {
            idx = i;
        }
    }
    if (idx === -1) {
        return ans;
    }
    const dfs = (i: number): void => {
        if (vis[i]) {
            return;
        }
        vis[i] = true;
        if (nums[i] < has.length) {
            has[nums[i]] = true;
        }
        for (const j of g[i]) {
            dfs(j);
        }
    };
    for (let i = 2; ~idx; idx = parents[idx]) {
        dfs(idx);
        while (has[i]) {
            ++i;
        }
        ans[idx] = i;
    }
    return ans;
}

Rust

impl Solution {
    pub fn smallest_missing_value_subtree(parents: Vec<i32>, nums: Vec<i32>) -> Vec<i32> {
        fn dfs(
            i: usize,
            vis: &mut Vec<bool>,
            has: &mut Vec<bool>,
            g: &Vec<Vec<usize>>,
            nums: &Vec<i32>,
        ) {
            if vis[i] {
                return;
            }
            vis[i] = true;
            if nums[i] < (has.len() as i32) {
                has[nums[i] as usize] = true;
            }
            for &j in &g[i] {
                dfs(j, vis, has, g, nums);
            }
        }

        let n = nums.len();
        let mut ans = vec![1; n];
        let mut g: Vec<Vec<usize>> = vec![vec![]; n];
        let mut idx = -1;
        for (i, &p) in parents.iter().enumerate() {
            if i > 0 {
                g[p as usize].push(i);
            }
            if nums[i] == 1 {
                idx = i as i32;
            }
        }
        if idx == -1 {
            return ans;
        }
        let mut vis = vec![false; n];
        let mut has = vec![false; (n + 2) as usize];
        let mut i = 2;
        let mut idx_mut = idx;
        while idx_mut != -1 {
            dfs(idx_mut as usize, &mut vis, &mut has, &g, &nums);
            while has[i] {
                i += 1;
            }
            ans[idx_mut as usize] = i as i32;
            idx_mut = parents[idx_mut as usize];
        }
        ans
    }
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

2003. 每棵子树内缺失的最小基因值

题目描述

解法

方法一：DFS

Python3

Java

C++

Go

TypeScript

Rust

Files

README.md

Latest commit

History

README.md

File metadata and controls

2003. 每棵子树内缺失的最小基因值

题目描述

解法

方法一：DFS

Python3

Java

C++

Go

TypeScript

Rust