Skip to content

Latest commit

 

History

History
188 lines (152 loc) · 7.27 KB

README.md

File metadata and controls

188 lines (152 loc) · 7.27 KB
Raw
comments difficulty edit_url rating source tags
true
中等
1969
第 57 场双周赛 Q3
数组
哈希表
前缀和
排序

1943. 描述绘画结果

English Version

题目描述

给你一个细长的画，用数轴表示。这幅画由若干有重叠的线段表示，每个线段有 独一无二 的颜色。给你二维整数数组 segments ，其中 segments[i] = [starti, endi, colori] 表示线段为 半开区间 [starti, endi) 且颜色为 colori 。

线段间重叠部分的颜色会被 混合 。如果有两种或者更多颜色混合时，它们会形成一种新的颜色，用一个 集合 表示这个混合颜色。

  • 比方说，如果颜色 2 ，4 和 6 被混合，那么结果颜色为 {2,4,6} 。

为了简化题目，你不需要输出整个集合，只需要用集合中所有元素的 和 来表示颜色集合。

你想要用 最少数目 不重叠 半开区间 来 表示 这幅混合颜色的画。这些线段可以用二维数组 painting 表示，其中 painting[j] = [leftj, rightj, mixj] 表示一个 半开区间[leftj, rightj) 的颜色 和 为 mixj 。

  • 比方说，这幅画由 segments = [[1,4,5],[1,7,7]] 组成，那么它可以表示为 painting = [[1,4,12],[4,7,7]] ，因为： 
    <ul>
	<li><code>[1,4)</code>&nbsp;由颜色&nbsp;<code>{5,7}</code>&nbsp;组成（和为&nbsp;<code>12</code>），分别来自第一个线段和第二个线段。</li>
	<li><code>[4,7)</code>&nbsp;由颜色 <code>{7}</code>&nbsp;组成，来自第二个线段。</li>
</ul>
</li>

请你返回二维数组 painting ，它表示最终绘画的结果（没有 被涂色的部分不出现在结果中）。你可以按 任意顺序 返回最终数组的结果。

半开区间 [a, b) 是数轴上点 a 和点 b 之间的部分，包含 点 a 且 不包含 点 b 。

 

示例 1：

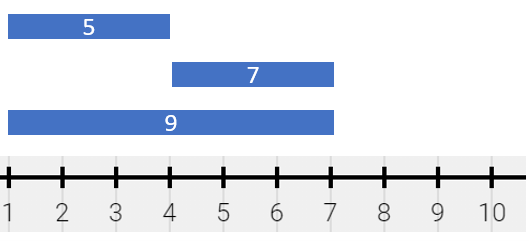
输入：segments = [[1,4,5],[4,7,7],[1,7,9]]
输出：[[1,4,14],[4,7,16]]
解释：绘画结果可以表示为：
- [1,4) 颜色为 {5,9} （和为 14），分别来自第一和第二个线段。
- [4,7) 颜色为 {7,9} （和为 16），分别来自第二和第三个线段。

示例 2：

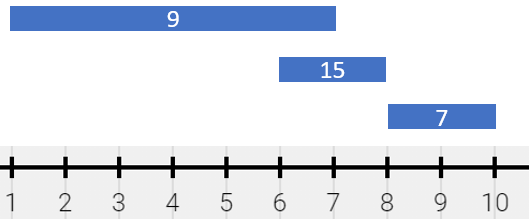
输入：segments = [[1,7,9],[6,8,15],[8,10,7]]
输出：[[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
解释：绘画结果可以以表示为：
- [1,6) 颜色为 9 ，来自第一个线段。
- [6,7) 颜色为 {9,15} （和为 24），来自第一和第二个线段。
- [7,8) 颜色为 15 ，来自第二个线段。
- [8,10) 颜色为 7 ，来自第三个线段。

示例 3：

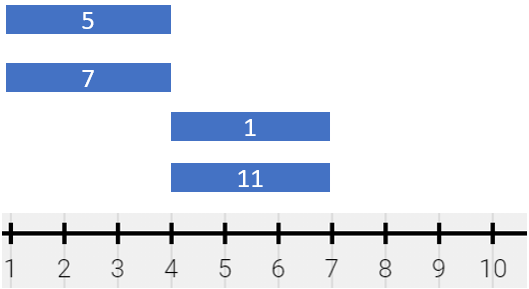
输入：segments = [[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
输出：[[1,4,12],[4,7,12]]
解释：绘画结果可以表示为：
- [1,4) 颜色为 {5,7} （和为 12），分别来自第一和第二个线段。
- [4,7) 颜色为 {1,11} （和为 12），分别来自第三和第四个线段。
注意，只返回一个单独的线段 [1,7) 是不正确的，因为混合颜色的集合不相同。

 

提示：

  • 1 <= segments.length <= 2 * 104
  • segments[i].length == 3
  • 1 <= starti < endi <= 105
  • 1 <= colori <= 109
  • 每种颜色 colori 互不相同。

解法

方法一：差分数组

Python3

class Solution:
    def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:
        d = defaultdict(int)
        for l, r, c in segments:
            d[l] += c
            d[r] -= c
        s = sorted([[k, v] for k, v in d.items()])
        n = len(s)
        for i in range(1, n):
            s[i][1] += s[i - 1][1]
        return [[s[i][0], s[i + 1][0], s[i][1]] for i in range(n - 1) if s[i][1]]

Java

class Solution {
    public List<List<Long>> splitPainting(int[][] segments) {
        TreeMap<Integer, Long> d = new TreeMap<>();
        for (int[] e : segments) {
            int l = e[0], r = e[1], c = e[2];
            d.put(l, d.getOrDefault(l, 0L) + c);
            d.put(r, d.getOrDefault(r, 0L) - c);
        }
        List<List<Long>> ans = new ArrayList<>();
        long i = 0, j = 0;
        long cur = 0;
        for (Map.Entry<Integer, Long> e : d.entrySet()) {
            if (Objects.equals(e.getKey(), d.firstKey())) {
                i = e.getKey();
            } else {
                j = e.getKey();
                if (cur > 0) {
                    ans.add(Arrays.asList(i, j, cur));
                }
                i = j;
            }
            cur += e.getValue();
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<vector<long long>> splitPainting(vector<vector<int>>& segments) {
        map<int, long long> d;
        for (auto& e : segments) {
            int l = e[0], r = e[1], c = e[2];
            d[l] += c;
            d[r] -= c;
        }
        vector<vector<long long>> ans;
        long long i, j, cur = 0;
        for (auto& it : d) {
            if (it == *d.begin())
                i = it.first;
            else {
                j = it.first;
                if (cur > 0) ans.push_back({i, j, cur});
                i = j;
            }
            cur += it.second;
        }
        return ans;
    }
};