Skip to content

Latest commit

 

History

History
234 lines (193 loc) · 7.11 KB

README.md

File metadata and controls

234 lines (193 loc) · 7.11 KB
Raw
comments difficulty edit_url rating source tags
true
中等
2105
第 250 场周赛 Q3
数组
动态规划

1937. 扣分后的最大得分

English Version

题目描述

给你一个 m x n 的整数矩阵 points （下标从 0 开始）。一开始你的得分为 0 ，你想最大化从矩阵中得到的分数。

你的得分方式为：每一行 中选取一个格子，选中坐标为 (r, c) 的格子会给你的总得分 增加 points[r][c] 。

然而，相邻行之间被选中的格子如果隔得太远，你会失去一些得分。对于相邻行 r 和 r + 1 （其中 0 <= r < m - 1），选中坐标为 (r, c1) 和 (r + 1, c2) 的格子，你的总得分 减少 abs(c1 - c2) 。

请你返回你能得到的 最大 得分。

abs(x) 定义为：

  • 如果 x >= 0 ，那么值为 x 。
  • 如果 x < 0 ，那么值为 -x 。

 

示例 1：

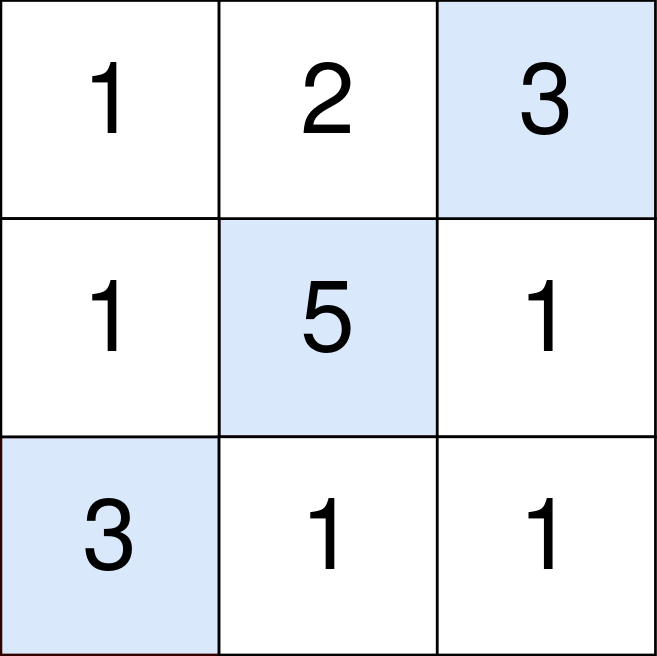
输入：points = [[1,2,3],[1,5,1],[3,1,1]]
输出：9
解释：
蓝色格子是最优方案选中的格子，坐标分别为 (0, 2)，(1, 1) 和 (2, 0) 。
你的总得分增加 3 + 5 + 3 = 11 。
但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。
你的最终得分为 11 - 2 = 9 。

示例 2：

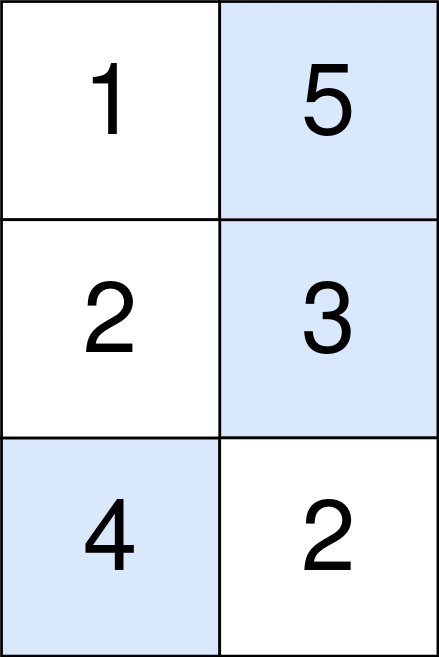
输入：points = [[1,5],[2,3],[4,2]]
输出：11
解释：
蓝色格子是最优方案选中的格子，坐标分别为 (0, 1)，(1, 1) 和 (2, 0) 。
你的总得分增加 5 + 3 + 4 = 12 。
但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。
你的最终得分为 12 - 1 = 11 。

 

提示：

  • m == points.length
  • n == points[r].length
  • 1 <= m, n <= 105
  • 1 <= m * n <= 105
  • 0 <= points[r][c] <= 105

解法

方法一：动态规划

我们定义 $f[i][j]$ 表示选取前 $i-1$ 行，并且第 $i-1$ 行选择第 $j$ 列的格子时的最大得分。初始时 $f[0][j] = points[0][j]$。

对于 $i &gt; 0$ 的情况，对于 $f[i][j]$，我们考虑是从上一行的哪一列转移过来的，记上一行选择的列为 $k$，那么有：

$$ f[i][j]= \begin{cases} \max(f[i - 1][k] + k - j + points[i][j]), & 0 \le k < j \\ \max(f[i - 1][k] - k + j + points[i][j]), & j < k < n \end{cases} $$

其中 $n$ 表示列数。答案为 $\max\limits_{0 \le j &lt; n} f[m - 1][j]$。

我们注意到 $f[i]$ 的值只跟 $f[i-1]$ 的值有关，因此我们可以使用滚动数组优化空间复杂度。

时间复杂度 $O(m \times n)$，空间复杂度 $O(n)$。其中 $m$ 和 $n$ 分别是矩阵的行数和列数。

Python3

class Solution:
    def maxPoints(self, points: List[List[int]]) -> int:
        n = len(points[0])
        f = points[0][:]
        for p in points[1:]:
            g = [0] * n
            lmx = -inf
            for j in range(n):
                lmx = max(lmx, f[j] + j)
                g[j] = max(g[j], p[j] + lmx - j)
            rmx = -inf
            for j in range(n - 1, -1, -1):
                rmx = max(rmx, f[j] - j)
                g[j] = max(g[j], p[j] + rmx + j)
            f = g
        return max(f)

Java

class Solution {
    public long maxPoints(int[][] points) {
        int n = points[0].length;
        long[] f = new long[n];
        final long inf = 1L << 60;
        for (int[] p : points) {
            long[] g = new long[n];
            long lmx = -inf, rmx = -inf;
            for (int j = 0; j < n; ++j) {
                lmx = Math.max(lmx, f[j] + j);
                g[j] = Math.max(g[j], p[j] + lmx - j);
            }
            for (int j = n - 1; j >= 0; --j) {
                rmx = Math.max(rmx, f[j] - j);
                g[j] = Math.max(g[j], p[j] + rmx + j);
            }
            f = g;
        }
        long ans = 0;
        for (long x : f) {
            ans = Math.max(ans, x);
        }
        return ans;
    }
}

C++

class Solution {
public:
    long long maxPoints(vector<vector<int>>& points) {
        using ll = long long;
        int n = points[0].size();
        vector<ll> f(n);
        const ll inf = 1e18;
        for (auto& p : points) {
            vector<ll> g(n);
            ll lmx = -inf, rmx = -inf;
            for (int j = 0; j < n; ++j) {
                lmx = max(lmx, f[j] + j);
                g[j] = max(g[j], p[j] + lmx - j);
            }
            for (int j = n - 1; ~j; --j) {
                rmx = max(rmx, f[j] - j);
                g[j] = max(g[j], p[j] + rmx + j);
            }
            f = move(g);
        }
        return *max_element(f.begin(), f.end());
    }
};

Go

func maxPoints(points [][]int) int64 {
	n := len(points[0])
	const inf int64 = 1e18
	f := make([]int64, n)
	for _, p := range points {
		g := make([]int64, n)
		lmx, rmx := -inf, -inf
		for j := range p {
			lmx = max(lmx, f[j]+int64(j))
			g[j] = max(g[j], int64(p[j])+lmx-int64(j))
		}
		for j := n - 1; j >= 0; j-- {
			rmx = max(rmx, f[j]-int64(j))
			g[j] = max(g[j], int64(p[j])+rmx+int64(j))
		}
		f = g
	}
	return slices.Max(f)
}

TypeScript

function maxPoints(points: number[][]): number {
    const n = points[0].length;
    const f: number[] = new Array(n).fill(0);
    for (const p of points) {
        const g: number[] = new Array(n).fill(0);
        let lmx = -Infinity;
        let rmx = -Infinity;
        for (let j = 0; j < n; ++j) {
            lmx = Math.max(lmx, f[j] + j);
            g[j] = Math.max(g[j], p[j] + lmx - j);
        }
        for (let j = n - 1; ~j; --j) {
            rmx = Math.max(rmx, f[j] - j);
            g[j] = Math.max(g[j], p[j] + rmx + j);
        }
        f.splice(0, n, ...g);
    }
    return Math.max(...f);
}