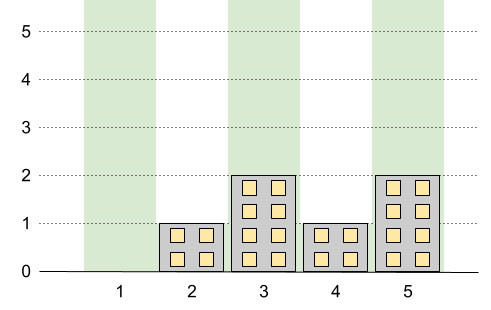Skip to content

Latest commit

 

History

History
197 lines (165 loc) · 6.68 KB

README_EN.md

File metadata and controls

197 lines (165 loc) · 6.68 KB
Raw
comments difficulty edit_url rating source tags
true
Hard
2374
Weekly Contest 238 Q4
Array
Math
Sorting

1840. Maximum Building Height

中文文档

Description

You want to build n new buildings in a city. The new buildings will be built in a line and are labeled from 1 to n.

However, there are city restrictions on the heights of the new buildings:

  • The height of each building must be a non-negative integer.
  • The height of the first building must be 0.
  • The height difference between any two adjacent buildings cannot exceed 1.

Additionally, there are city restrictions on the maximum height of specific buildings. These restrictions are given as a 2D integer array restrictions where restrictions[i] = [idi, maxHeighti] indicates that building idi must have a height less than or equal to maxHeighti.

It is guaranteed that each building will appear at most once in restrictions, and building 1 will not be in restrictions.

Return the maximum possible height of the tallest building.

 

Example 1:

Input: n = 5, restrictions = [[2,1],[4,1]]
Output: 2
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,1,2], and the tallest building has a height of 2.

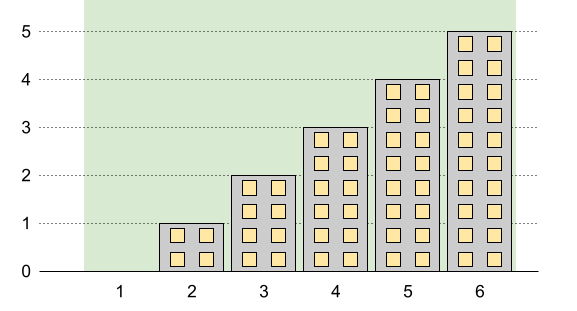
Example 2:

Input: n = 6, restrictions = []
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,4,5], and the tallest building has a height of 5.

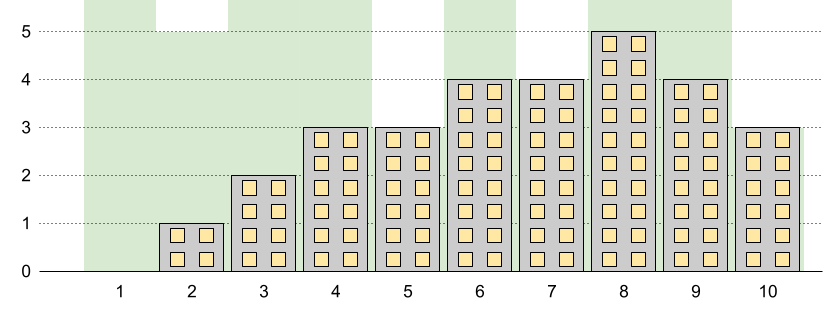
Example 3:

Input: n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,3,4,4,5,4,3], and the tallest building has a height of 5.

 

Constraints:

  • 2 <= n <= 109
  • 0 <= restrictions.length <= min(n - 1, 105)
  • 2 <= idi <= n
  • idi is unique.
  • 0 <= maxHeighti <= 109

Solutions

Solution 1

Python3

class Solution:
    def maxBuilding(self, n: int, restrictions: List[List[int]]) -> int:
        r = restrictions
        r.append([1, 0])
        r.sort()
        if r[-1][0] != n:
            r.append([n, n - 1])
        m = len(r)
        for i in range(1, m):
            r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0])
        for i in range(m - 2, 0, -1):
            r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0])
        ans = 0
        for i in range(m - 1):
            t = (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) // 2
            ans = max(ans, t)
        return ans

Java

class Solution {
    public int maxBuilding(int n, int[][] restrictions) {
        List<int[]> r = new ArrayList<>();
        r.addAll(Arrays.asList(restrictions));
        r.add(new int[] {1, 0});
        Collections.sort(r, (a, b) -> a[0] - b[0]);
        if (r.get(r.size() - 1)[0] != n) {
            r.add(new int[] {n, n - 1});
        }
        int m = r.size();
        for (int i = 1; i < m; ++i) {
            int[] a = r.get(i - 1), b = r.get(i);
            b[1] = Math.min(b[1], a[1] + b[0] - a[0]);
        }
        for (int i = m - 2; i > 0; --i) {
            int[] a = r.get(i), b = r.get(i + 1);
            a[1] = Math.min(a[1], b[1] + b[0] - a[0]);
        }
        int ans = 0;
        for (int i = 0; i < m - 1; ++i) {
            int[] a = r.get(i), b = r.get(i + 1);
            int t = (a[1] + b[1] + b[0] - a[0]) / 2;
            ans = Math.max(ans, t);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maxBuilding(int n, vector<vector<int>>& restrictions) {
        auto&& r = restrictions;
        r.push_back({1, 0});
        sort(r.begin(), r.end());
        if (r[r.size() - 1][0] != n) r.push_back({n, n - 1});
        int m = r.size();
        for (int i = 1; i < m; ++i) {
            r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0]);
        }
        for (int i = m - 2; i > 0; --i) {
            r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0]);
        }
        int ans = 0;
        for (int i = 0; i < m - 1; ++i) {
            int t = (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) / 2;
            ans = max(ans, t);
        }
        return ans;
    }
};

Go

func maxBuilding(n int, restrictions [][]int) (ans int) {
	r := restrictions
	r = append(r, []int{1, 0})
	sort.Slice(r, func(i, j int) bool { return r[i][0] < r[j][0] })
	if r[len(r)-1][0] != n {
		r = append(r, []int{n, n - 1})
	}
	m := len(r)
	for i := 1; i < m; i++ {
		r[i][1] = min(r[i][1], r[i-1][1]+r[i][0]-r[i-1][0])
	}
	for i := m - 2; i > 0; i-- {
		r[i][1] = min(r[i][1], r[i+1][1]+r[i+1][0]-r[i][0])
	}
	for i := 0; i < m-1; i++ {
		t := (r[i][1] + r[i+1][1] + r[i+1][0] - r[i][0]) / 2
		ans = max(ans, t)
	}
	return ans
}