README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/1700-1799/1727.Largest%20Submatrix%20With%20Rearrangements/README_EN.md	1926	Weekly Contest 224 Q3	Greedy Array Matrix Sorting

1727. Largest Submatrix With Rearrangements

中文文档

Description

You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.

Return the area of the largest submatrix within matrix where every element of the submatrix is 1 after reordering the columns optimally.

 

Example 1:

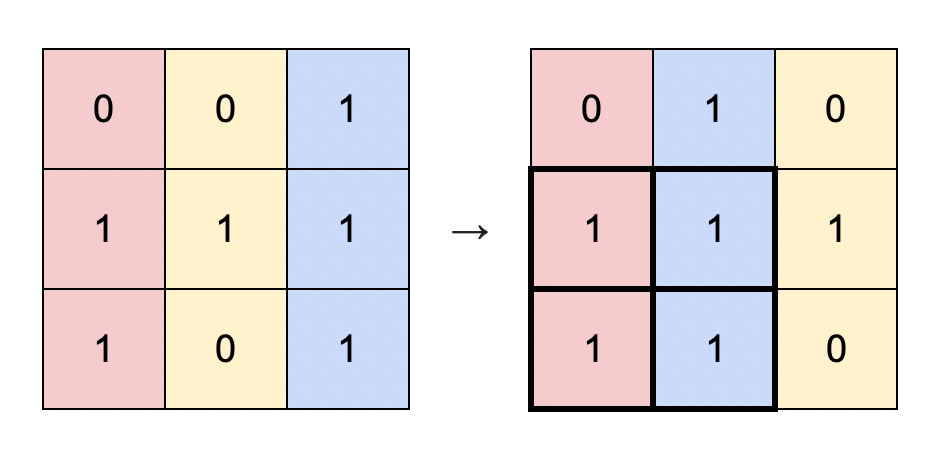
Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.

Example 2:

Input: matrix = [[1,0,1,0,1]]
Output: 3
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 3.

Example 3:

Input: matrix = [[1,1,0],[1,0,1]]
Output: 2
Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m * n <= 105
• matrix[i][j] is either 0 or 1.

Solutions

Solution 1: Preprocessing + Sorting

Since the matrix is rearranged by columns according to the problem, we can first preprocess each column of the matrix.

For each element with a value of $1$, we update its value to the maximum consecutive number of $1$s above it, that is, $matrix[i][j] = matrix[i-1][j] + 1$.

Next, we can sort each row of the updated matrix. Then traverse each row, calculate the area of the largest sub-matrix full of $1$s with this row as the bottom edge. The specific calculation logic is as follows:

For a row of the matrix, we denote the value of the $k$-th largest element as $val_k$, where $k \geq 1$, then there are at least $k$ elements in this row that are not less than $val_k$, forming a sub-matrix full of $1$s with an area of $val_k \times k$. Traverse each element of this row from large to small, take the maximum value of $val_k \times k$, and update the answer.

The time complexity is $O(m \times n \times \log n)$. Here, $m$ and $n$ are the number of rows and columns of the matrix, respectively.

Python3

class Solution:
    def largestSubmatrix(self, matrix: List[List[int]]) -> int:
        for i in range(1, len(matrix)):
            for j in range(len(matrix[0])):
                if matrix[i][j]:
                    matrix[i][j] = matrix[i - 1][j] + 1
        ans = 0
        for row in matrix:
            row.sort(reverse=True)
            for j, v in enumerate(row, 1):
                ans = max(ans, j * v)
        return ans

Java

class Solution {
    public int largestSubmatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        for (int i = 1; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == 1) {
                    matrix[i][j] = matrix[i - 1][j] + 1;
                }
            }
        }
        int ans = 0;
        for (var row : matrix) {
            Arrays.sort(row);
            for (int j = n - 1, k = 1; j >= 0 && row[j] > 0; --j, ++k) {
                int s = row[j] * k;
                ans = Math.max(ans, s);
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int largestSubmatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        for (int i = 1; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j]) {
                    matrix[i][j] = matrix[i - 1][j] + 1;
                }
            }
        }
        int ans = 0;
        for (auto& row : matrix) {
            sort(row.rbegin(), row.rend());
            for (int j = 0; j < n; ++j) {
                ans = max(ans, (j + 1) * row[j]);
            }
        }
        return ans;
    }
};

Go

func largestSubmatrix(matrix [][]int) int {
	m, n := len(matrix), len(matrix[0])
	for i := 1; i < m; i++ {
		for j := 0; j < n; j++ {
			if matrix[i][j] == 1 {
				matrix[i][j] = matrix[i-1][j] + 1
			}
		}
	}
	ans := 0
	for _, row := range matrix {
		sort.Ints(row)
		for j, k := n-1, 1; j >= 0 && row[j] > 0; j, k = j-1, k+1 {
			ans = max(ans, row[j]*k)
		}
	}
	return ans
}

TypeScript

function largestSubmatrix(matrix: number[][]): number {
    for (let column = 0; column < matrix[0].length; column++) {
        for (let row = 0; row < matrix.length; row++) {
            let tempRow = row;
            let count = 0;

            while (tempRow < matrix.length && matrix[tempRow][column] === 1) {
                count++;
                tempRow++;
            }

            while (count !== 0) {
                matrix[row][column] = count;
                count--;
                row++;
            }
        }
    }

    for (let row = 0; row < matrix.length; row++) {
        matrix[row].sort((a, b) => a - b);
    }

    let maxSubmatrixArea = 0;

    for (let row = 0; row < matrix.length; row++) {
        for (let col = matrix[row].length - 1; col >= 0; col--) {
            maxSubmatrixArea = Math.max(
                maxSubmatrixArea,
                matrix[row][col] * (matrix[row].length - col),
            );
        }
    }

    return maxSubmatrixArea;
}