Skip to content

Latest commit

 

History

History
306 lines (255 loc) · 9.38 KB

README_EN.md

File metadata and controls

306 lines (255 loc) · 9.38 KB
Raw
comments difficulty edit_url rating source tags
true
Hard
2116
Weekly Contest 201 Q4
Array
Dynamic Programming
Sorting

1547. Minimum Cost to Cut a Stick

中文文档

Description

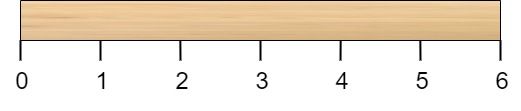
Given a wooden stick of length n units. The stick is labelled from 0 to n. For example, a stick of length 6 is labelled as follows:

Given an integer array cuts where cuts[i] denotes a position you should perform a cut at.

You should perform the cuts in order, you can change the order of the cuts as you wish.

The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.

Return the minimum total cost of the cuts.

 

Example 1:

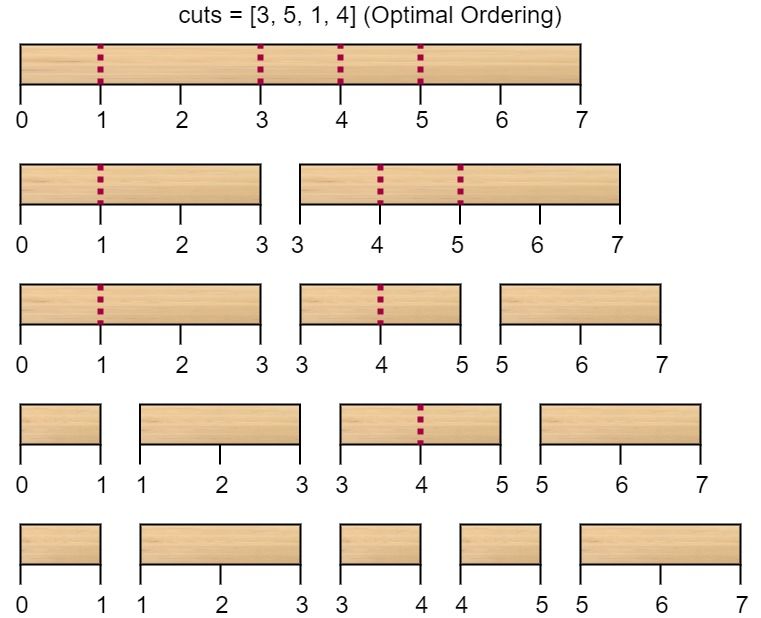
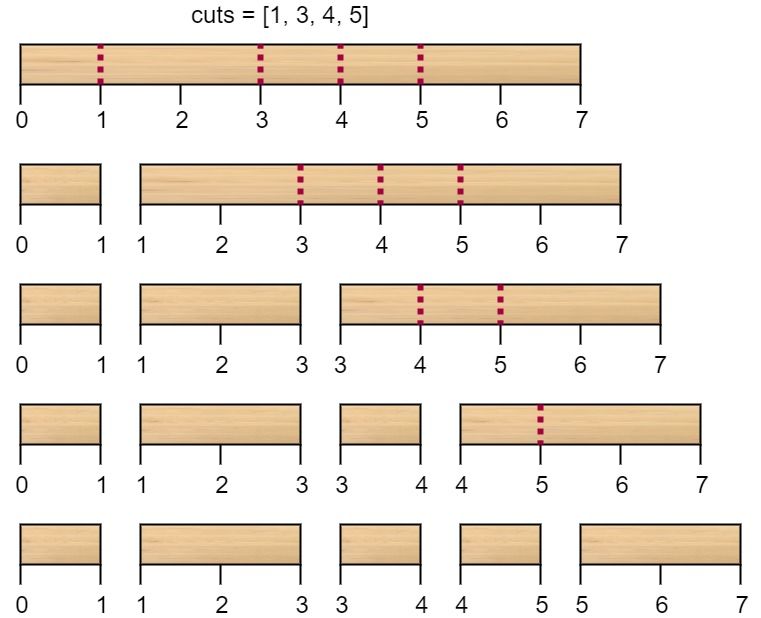
Input: n = 7, cuts = [1,3,4,5]
Output: 16
Explanation: Using cuts order = [1, 3, 4, 5] as in the input leads to the following scenario:

The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be [3, 5, 1, 4] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).

Example 2:

Input: n = 9, cuts = [5,6,1,4,2]
Output: 22
Explanation: If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order [4, 6, 5, 2, 1] has total cost = 22 which is the minimum possible.

 

Constraints:

  • 2 <= n <= 106
  • 1 <= cuts.length <= min(n - 1, 100)
  • 1 <= cuts[i] <= n - 1
  • All the integers in cuts array are distinct.

Solutions

Solution 1: Dynamic Programming (Interval DP)

We can add two elements to the cut array $cuts$, which are $0$ and $n$, representing the two ends of the stick. Then we sort the $cuts$ array, so that we can cut the entire stick into several intervals, each interval has two cut points. Suppose the length of the $cuts$ array at this time is $m$.

Next, we define $f[i][j]$ to represent the minimum cost of cutting the interval $[cuts[i],..cuts[j]]$.

If an interval only has two cut points, that is, we do not need to cut this interval, then $f[i][j] = 0$.

Otherwise, we enumerate the length of the interval $l$, where $l$ is the number of cut points minus $1$. Then we enumerate the left endpoint $i$ of the interval, and the right endpoint $j$ can be obtained by $i + l$. For each interval, we enumerate its cut point $k$, where $i \lt k \lt j$, then we can cut the interval $[i, j]$ into $[i, k]$ and $[k, j]$, the cost at this time is $f[i][k] + f[k][j] + cuts[j] - cuts[i]$, we take the minimum value of all possible $k$, which is the value of $f[i][j]$.

Finally, we return $f[0][m - 1]$.

The time complexity is $O(m^3)$, and the space complexity is $O(m^2)$. Here, $m$ is the length of the modified $cuts$ array.

Python3

class Solution:
    def minCost(self, n: int, cuts: List[int]) -> int:
        cuts.extend([0, n])
        cuts.sort()
        m = len(cuts)
        f = [[0] * m for _ in range(m)]
        for l in range(2, m):
            for i in range(m - l):
                j = i + l
                f[i][j] = inf
                for k in range(i + 1, j):
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i])
        return f[0][-1]

Java

class Solution {
    public int minCost(int n, int[] cuts) {
        List<Integer> nums = new ArrayList<>();
        for (int x : cuts) {
            nums.add(x);
        }
        nums.add(0);
        nums.add(n);
        Collections.sort(nums);
        int m = nums.size();
        int[][] f = new int[m][m];
        for (int l = 2; l < m; ++l) {
            for (int i = 0; i + l < m; ++i) {
                int j = i + l;
                f[i][j] = 1 << 30;
                for (int k = i + 1; k < j; ++k) {
                    f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + nums.get(j) - nums.get(i));
                }
            }
        }
        return f[0][m - 1];
    }
}

C++

class Solution {
public:
    int minCost(int n, vector<int>& cuts) {
        cuts.push_back(0);
        cuts.push_back(n);
        sort(cuts.begin(), cuts.end());
        int m = cuts.size();
        int f[110][110]{};
        for (int l = 2; l < m; ++l) {
            for (int i = 0; i + l < m; ++i) {
                int j = i + l;
                f[i][j] = 1 << 30;
                for (int k = i + 1; k < j; ++k) {
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i]);
                }
            }
        }
        return f[0][m - 1];
    }
};

Go

func minCost(n int, cuts []int) int {
	cuts = append(cuts, []int{0, n}...)
	sort.Ints(cuts)
	m := len(cuts)
	f := make([][]int, m)
	for i := range f {
		f[i] = make([]int, m)
	}
	for l := 2; l < m; l++ {
		for i := 0; i+l < m; i++ {
			j := i + l
			f[i][j] = 1 << 30
			for k := i + 1; k < j; k++ {
				f[i][j] = min(f[i][j], f[i][k]+f[k][j]+cuts[j]-cuts[i])
			}
		}
	}
	return f[0][m-1]
}

TypeScript

function minCost(n: number, cuts: number[]): number {
    cuts.push(0);
    cuts.push(n);
    cuts.sort((a, b) => a - b);
    const m = cuts.length;
    const f: number[][] = new Array(m).fill(0).map(() => new Array(m).fill(0));
    for (let i = m - 2; i >= 0; --i) {
        for (let j = i + 2; j < m; ++j) {
            f[i][j] = 1 << 30;
            for (let k = i + 1; k < j; ++k) {
                f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i]);
            }
        }
    }
    return f[0][m - 1];
}

Solution 2

Python3

class Solution:
    def minCost(self, n: int, cuts: List[int]) -> int:
        cuts.extend([0, n])
        cuts.sort()
        m = len(cuts)
        f = [[0] * m for _ in range(m)]
        for i in range(m - 1, -1, -1):
            for j in range(i + 2, m):
                f[i][j] = inf
                for k in range(i + 1, j):
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i])
        return f[0][-1]

Java

class Solution {
    public int minCost(int n, int[] cuts) {
        List<Integer> nums = new ArrayList<>();
        for (int x : cuts) {
            nums.add(x);
        }
        nums.add(0);
        nums.add(n);
        Collections.sort(nums);
        int m = nums.size();
        int[][] f = new int[m][m];
        for (int i = m - 1; i >= 0; --i) {
            for (int j = i + 2; j < m; ++j) {
                f[i][j] = 1 << 30;
                for (int k = i + 1; k < j; ++k) {
                    f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + nums.get(j) - nums.get(i));
                }
            }
        }
        return f[0][m - 1];
    }
}

C++

class Solution {
public:
    int minCost(int n, vector<int>& cuts) {
        cuts.push_back(0);
        cuts.push_back(n);
        sort(cuts.begin(), cuts.end());
        int m = cuts.size();
        int f[110][110]{};
        for (int i = m - 1; ~i; --i) {
            for (int j = i + 2; j < m; ++j) {
                f[i][j] = 1 << 30;
                for (int k = i + 1; k < j; ++k) {
                    f[i][j] = min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i]);
                }
            }
        }
        return f[0][m - 1];
    }
};

Go

func minCost(n int, cuts []int) int {
	cuts = append(cuts, []int{0, n}...)
	sort.Ints(cuts)
	m := len(cuts)
	f := make([][]int, m)
	for i := range f {
		f[i] = make([]int, m)
	}
	for i := m - 1; i >= 0; i-- {
		for j := i + 2; j < m; j++ {
			f[i][j] = 1 << 30
			for k := i + 1; k < j; k++ {
				f[i][j] = min(f[i][j], f[i][k]+f[k][j]+cuts[j]-cuts[i])
			}
		}
	}
	return f[0][m-1]
}