README.md

comments	difficulty	edit_url	rating	source	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/1500-1599/1530.Number%20of%20Good%20Leaf%20Nodes%20Pairs/README.md	1745	第 199 场周赛 Q3	树 深度优先搜索 二叉树

1530. 好叶子节点对的数量

English Version

题目描述

给你二叉树的根节点 root 和一个整数 distance 。

如果二叉树中两个 叶 节点之间的 最短路径长度 小于或者等于 distance ，那它们就可以构成一组 好叶子节点对 。

返回树中 好叶子节点对的数量 。

 

示例 1：

 

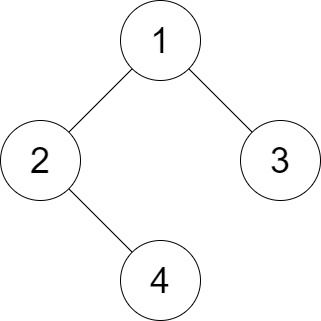
输入：root = [1,2,3,null,4], distance = 3
输出：1
解释：树的叶节点是 3 和 4 ，它们之间的最短路径的长度是 3 。这是唯一的好叶子节点对。

示例 2：

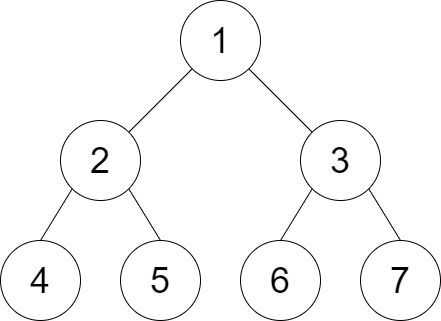
输入：root = [1,2,3,4,5,6,7], distance = 3
输出：2
解释：好叶子节点对为 [4,5] 和 [6,7] ，最短路径长度都是 2 。但是叶子节点对 [4,6] 不满足要求，因为它们之间的最短路径长度为 4 。

示例 3：

输入：root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
输出：1
解释：唯一的好叶子节点对是 [2,5] 。

示例 4：

输入：root = [100], distance = 1
输出：0

示例 5：

输入：root = [1,1,1], distance = 2
输出：1

 

提示：

• tree 的节点数在 [1, 2^10] 范围内。
• 每个节点的值都在 [1, 100] 之间。
• 1 <= distance <= 10

解法

方法一：递归

题目求一个二叉树好叶子节点的对数，答案可以拆分为三部分之和：左子树好叶子节点的对数、右子树好叶子节点的对数，以及左子树叶子节点与右子树叶子节点组成的好叶子节点的对数。

递归求解即可。

时间复杂度 $O(n \times distance^2 \times h)$，其中 $n$ 是二叉树的节点数，而 $h$ 是二叉树的高度。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countPairs(self, root: TreeNode, distance: int) -> int:
        def dfs(root, cnt, i):
            if root is None or i >= distance:
                return
            if root.left is None and root.right is None:
                cnt[i] += 1
                return
            dfs(root.left, cnt, i + 1)
            dfs(root.right, cnt, i + 1)

        if root is None:
            return 0
        ans = self.countPairs(root.left, distance) + self.countPairs(
            root.right, distance
        )
        cnt1 = Counter()
        cnt2 = Counter()
        dfs(root.left, cnt1, 1)
        dfs(root.right, cnt2, 1)

        for k1, v1 in cnt1.items():
            for k2, v2 in cnt2.items():
                if k1 + k2 <= distance:
                    ans += v1 * v2
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countPairs(TreeNode root, int distance) {
        if (root == null) {
            return 0;
        }
        int ans = countPairs(root.left, distance) + countPairs(root.right, distance);
        int[] cnt1 = new int[distance];
        int[] cnt2 = new int[distance];
        dfs(root.left, cnt1, 1);
        dfs(root.right, cnt2, 1);
        for (int i = 0; i < distance; ++i) {
            for (int j = 0; j < distance; ++j) {
                if (i + j <= distance) {
                    ans += cnt1[i] * cnt2[j];
                }
            }
        }
        return ans;
    }

    void dfs(TreeNode root, int[] cnt, int i) {
        if (root == null || i >= cnt.length) {
            return;
        }
        if (root.left == null && root.right == null) {
            ++cnt[i];
            return;
        }
        dfs(root.left, cnt, i + 1);
        dfs(root.right, cnt, i + 1);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countPairs(TreeNode* root, int distance) {
        if (!root) return 0;
        int ans = countPairs(root->left, distance) + countPairs(root->right, distance);
        vector<int> cnt1(distance);
        vector<int> cnt2(distance);
        dfs(root->left, cnt1, 1);
        dfs(root->right, cnt2, 1);
        for (int i = 0; i < distance; ++i) {
            for (int j = 0; j < distance; ++j) {
                if (i + j <= distance) {
                    ans += cnt1[i] * cnt2[j];
                }
            }
        }
        return ans;
    }

    void dfs(TreeNode* root, vector<int>& cnt, int i) {
        if (!root || i >= cnt.size()) return;
        if (!root->left && !root->right) {
            ++cnt[i];
            return;
        }
        dfs(root->left, cnt, i + 1);
        dfs(root->right, cnt, i + 1);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func countPairs(root *TreeNode, distance int) int {
	if root == nil {
		return 0
	}
	ans := countPairs(root.Left, distance) + countPairs(root.Right, distance)
	cnt1 := make([]int, distance)
	cnt2 := make([]int, distance)
	dfs(root.Left, cnt1, 1)
	dfs(root.Right, cnt2, 1)
	for i, v1 := range cnt1 {
		for j, v2 := range cnt2 {
			if i+j <= distance {
				ans += v1 * v2
			}
		}
	}
	return ans
}

func dfs(root *TreeNode, cnt []int, i int) {
	if root == nil || i >= len(cnt) {
		return
	}
	if root.Left == nil && root.Right == nil {
		cnt[i]++
		return
	}
	dfs(root.Left, cnt, i+1)
	dfs(root.Right, cnt, i+1)
}