README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Hard	https://github.com/doocs/leetcode/edit/main/solution/1400-1499/1483.Kth%20Ancestor%20of%20a%20Tree%20Node/README_EN.md	2115	Weekly Contest 193 Q4	Tree Depth-First Search Breadth-First Search Design Binary Search Dynamic Programming

1483. Kth Ancestor of a Tree Node

中文文档

Description

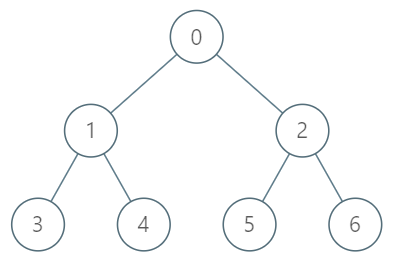
You are given a tree with n nodes numbered from 0 to n - 1 in the form of a parent array parent where parent[i] is the parent of ith node. The root of the tree is node 0. Find the kth ancestor of a given node.

The kth ancestor of a tree node is the kth node in the path from that node to the root node.

Implement the TreeAncestor class:

• TreeAncestor(int n, int[] parent) Initializes the object with the number of nodes in the tree and the parent array.
• int getKthAncestor(int node, int k) return the kth ancestor of the given node node. If there is no such ancestor, return -1.

 

Example 1:

Input
["TreeAncestor", "getKthAncestor", "getKthAncestor", "getKthAncestor"]
[[7, [-1, 0, 0, 1, 1, 2, 2]], [3, 1], [5, 2], [6, 3]]
Output
[null, 1, 0, -1]
Explanation
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor

 

Constraints:

• 1 <= k <= n <= 5 * 104
• parent.length == n
• parent[0] == -1
• 0 <= parent[i] < n for all 0 < i < n
• 0 <= node < n
• There will be at most 5 * 104 queries.

Solutions

Solution 1: Dynamic Programming + Binary Lifting

The problem asks us to find the $k$-th ancestor node of a node $node$. If we solve it by brute force, we need to traverse upwards from $node$ for $k$ times, which has a time complexity of $O(k)$ and will obviously exceed the time limit.

We can use dynamic programming combined with the idea of binary lifting to handle this.

We define $p[i][j]$ as the $2^j$-th ancestor node of node $i$, i.e., the node reached by moving $2^j$ steps upwards from node $i$. Then we can get the state transition equation:

$$ p[i][j] = p[p[i][j-1]][j-1] $$

That is, to find the $2^j$-th ancestor node of node $i$, we can first find the $2^{j-1}$-th ancestor node of node $i$, and then find the $2^{j-1}$-th ancestor node of this node. Therefore, we need to find the ancestor node of each node at a distance of $2^j$, until we reach the maximum height of the tree.

For each query later, we can decompose $k$ into its binary representation, and then according to the positions of $1$ in the binary, we accumulate the queries upwards, and finally get the $k$-th ancestor node of node $node$.

In terms of time complexity, the initialization is $O(n \times \log n)$, and the query is $O(\log n)$. The space complexity is $O(n \times \log n)$, where $n$ is the number of nodes in the tree.

Similar problems:

• 2836. Maximize Value of Function in a Ball Passing Game

Python3

class TreeAncestor:
    def __init__(self, n: int, parent: List[int]):
        self.p = [[-1] * 18 for _ in range(n)]
        for i, fa in enumerate(parent):
            self.p[i][0] = fa
        for j in range(1, 18):
            for i in range(n):
                if self.p[i][j - 1] == -1:
                    continue
                self.p[i][j] = self.p[self.p[i][j - 1]][j - 1]

    def getKthAncestor(self, node: int, k: int) -> int:
        for i in range(17, -1, -1):
            if k >> i & 1:
                node = self.p[node][i]
                if node == -1:
                    break
        return node


# Your TreeAncestor object will be instantiated and called as such:
# obj = TreeAncestor(n, parent)
# param_1 = obj.getKthAncestor(node,k)

Java

class TreeAncestor {
    private int[][] p;

    public TreeAncestor(int n, int[] parent) {
        p = new int[n][18];
        for (var e : p) {
            Arrays.fill(e, -1);
        }
        for (int i = 0; i < n; ++i) {
            p[i][0] = parent[i];
        }
        for (int j = 1; j < 18; ++j) {
            for (int i = 0; i < n; ++i) {
                if (p[i][j - 1] == -1) {
                    continue;
                }
                p[i][j] = p[p[i][j - 1]][j - 1];
            }
        }
    }

    public int getKthAncestor(int node, int k) {
        for (int i = 17; i >= 0; --i) {
            if (((k >> i) & 1) == 1) {
                node = p[node][i];
                if (node == -1) {
                    break;
                }
            }
        }
        return node;
    }
}

/**
 * Your TreeAncestor object will be instantiated and called as such:
 * TreeAncestor obj = new TreeAncestor(n, parent);
 * int param_1 = obj.getKthAncestor(node,k);
 */

C++

class TreeAncestor {
public:
    TreeAncestor(int n, vector<int>& parent) {
        p = vector<vector<int>>(n, vector<int>(18, -1));
        for (int i = 0; i < n; ++i) {
            p[i][0] = parent[i];
        }
        for (int j = 1; j < 18; ++j) {
            for (int i = 0; i < n; ++i) {
                if (p[i][j - 1] == -1) {
                    continue;
                }
                p[i][j] = p[p[i][j - 1]][j - 1];
            }
        }
    }

    int getKthAncestor(int node, int k) {
        for (int i = 17; ~i; --i) {
            if (k >> i & 1) {
                node = p[node][i];
                if (node == -1) {
                    break;
                }
            }
        }
        return node;
    }

private:
    vector<vector<int>> p;
};

/**
 * Your TreeAncestor object will be instantiated and called as such:
 * TreeAncestor* obj = new TreeAncestor(n, parent);
 * int param_1 = obj->getKthAncestor(node,k);
 */

Go

type TreeAncestor struct {
	p [][18]int
}

func Constructor(n int, parent []int) TreeAncestor {
	p := make([][18]int, n)
	for i, fa := range parent {
		p[i][0] = fa
		for j := 1; j < 18; j++ {
			p[i][j] = -1
		}
	}
	for j := 1; j < 18; j++ {
		for i := range p {
			if p[i][j-1] == -1 {
				continue
			}
			p[i][j] = p[p[i][j-1]][j-1]
		}
	}
	return TreeAncestor{p}
}

func (this *TreeAncestor) GetKthAncestor(node int, k int) int {
	for i := 17; i >= 0; i-- {
		if k>>i&1 == 1 {
			node = this.p[node][i]
			if node == -1 {
				break
			}
		}
	}
	return node
}

/**
 * Your TreeAncestor object will be instantiated and called as such:
 * obj := Constructor(n, parent);
 * param_1 := obj.GetKthAncestor(node,k);
 */

TypeScript

class TreeAncestor {
    private p: number[][];

    constructor(n: number, parent: number[]) {
        const p = new Array(n).fill(0).map(() => new Array(18).fill(-1));
        for (let i = 0; i < n; ++i) {
            p[i][0] = parent[i];
        }
        for (let j = 1; j < 18; ++j) {
            for (let i = 0; i < n; ++i) {
                if (p[i][j - 1] === -1) {
                    continue;
                }
                p[i][j] = p[p[i][j - 1]][j - 1];
            }
        }
        this.p = p;
    }

    getKthAncestor(node: number, k: number): number {
        for (let i = 17; i >= 0; --i) {
            if (((k >> i) & 1) === 1) {
                node = this.p[node][i];
                if (node === -1) {
                    break;
                }
            }
        }
        return node;
    }
}

/**
 * Your TreeAncestor object will be instantiated and called as such:
 * var obj = new TreeAncestor(n, parent)
 * var param_1 = obj.getKthAncestor(node,k)
 */

C#

public class TreeAncestor {
    private int[][] p;

    public TreeAncestor(int n, int[] parent) {
        p = new int[n][];
        for (int i = 0; i < n; i++) {
            p[i] = new int[18];
            for (int j = 0; j < 18; j++) {
                p[i][j] = -1;
            }
        }

        for (int i = 0; i < n; ++i) {
            p[i][0] = parent[i];
        }

        for (int j = 1; j < 18; ++j) {
            for (int i = 0; i < n; ++i) {
                if (p[i][j - 1] == -1) {
                    continue;
                }
                p[i][j] = p[p[i][j - 1]][j - 1];
            }
        }
    }

    public int GetKthAncestor(int node, int k) {
        for (int i = 17; i >= 0; --i) {
            if (((k >> i) & 1) == 1) {
                node = p[node][i];
                if (node == -1) {
                    break;
                }
            }
        }
        return node;
    }
}


/**
 * Your TreeAncestor object will be instantiated and called as such:
 * TreeAncestor obj = new TreeAncestor(n, parent);
 * int param_1 = obj.GetKthAncestor(node,k);
 */