README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/1300-1399/1386.Cinema%20Seat%20Allocation/README_EN.md	1636	Biweekly Contest 22 Q2	Greedy Bit Manipulation Array Hash Table

1386. Cinema Seat Allocation

中文文档

Description

A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.

Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i] = [3,8] means the seat located in row 3 and labelled with 8 is already reserved.

Return the maximum number of four-person groups you can assign on the cinema seats. A four-person group occupies four adjacent seats in one single row. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.

 

Example 1:

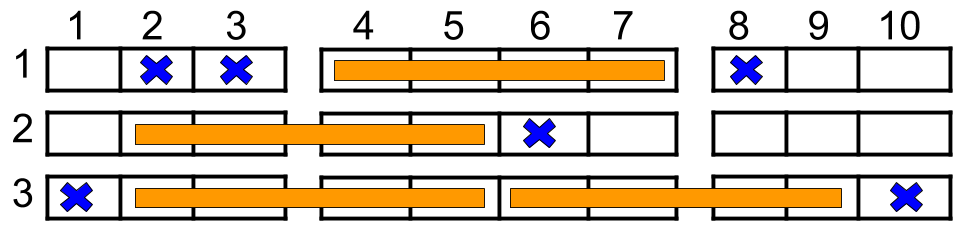
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.

Example 2:

Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2

Example 3:

Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4

 

Constraints:

• 1 <= n <= 10^9
• 1 <= reservedSeats.length <= min(10*n, 10^4)
• reservedSeats[i].length == 2
• 1 <= reservedSeats[i][0] <= n
• 1 <= reservedSeats[i][1] <= 10
• All reservedSeats[i] are distinct.

Solutions

Solution 1: Hash Table + Bit Manipulation

We use a hash table $d$ to store all the reserved seats, where the key is the row number, and the value is the state of the reserved seats in that row, i.e., a binary number. The $j$-th bit being $1$ means the $j$-th seat is reserved, and $0$ means the $j$-th seat is not reserved.

We traverse $reservedSeats$, for each seat $(i, j)$, we add the state of the $j$-th seat (corresponding to the $10-j$ bit in the lower bits) to $d[i]$.

For rows that do not appear in the hash table $d$, we can arrange $2$ families arbitrarily, so the initial answer is $(n - len(d)) \times 2$.

Next, we traverse the state of each row in the hash table. For each row, we try to arrange the situations $1234, 5678, 3456$ in turn. If a situation can be arranged, we add $1$ to the answer.

After the traversal, we get the final answer.

The time complexity is $O(m)$, and the space complexity is $O(m)$. Where $m$ is the length of $reservedSeats$.

Python3

class Solution:
    def maxNumberOfFamilies(self, n: int, reservedSeats: List[List[int]]) -> int:
        d = defaultdict(int)
        for i, j in reservedSeats:
            d[i] |= 1 << (10 - j)
        masks = (0b0111100000, 0b0000011110, 0b0001111000)
        ans = (n - len(d)) * 2
        for x in d.values():
            for mask in masks:
                if (x & mask) == 0:
                    x |= mask
                    ans += 1
        return ans

Java

class Solution {
    public int maxNumberOfFamilies(int n, int[][] reservedSeats) {
        Map<Integer, Integer> d = new HashMap<>();
        for (var e : reservedSeats) {
            int i = e[0], j = e[1];
            d.merge(i, 1 << (10 - j), (x, y) -> x | y);
        }
        int[] masks = {0b0111100000, 0b0000011110, 0b0001111000};
        int ans = (n - d.size()) * 2;
        for (int x : d.values()) {
            for (int mask : masks) {
                if ((x & mask) == 0) {
                    x |= mask;
                    ++ans;
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maxNumberOfFamilies(int n, vector<vector<int>>& reservedSeats) {
        unordered_map<int, int> d;
        for (auto& e : reservedSeats) {
            int i = e[0], j = e[1];
            d[i] |= 1 << (10 - j);
        }
        int masks[3] = {0b0111100000, 0b0000011110, 0b0001111000};
        int ans = (n - d.size()) * 2;
        for (auto& [_, x] : d) {
            for (int& mask : masks) {
                if ((x & mask) == 0) {
                    x |= mask;
                    ++ans;
                }
            }
        }
        return ans;
    }
};

Go

func maxNumberOfFamilies(n int, reservedSeats [][]int) int {
	d := map[int]int{}
	for _, e := range reservedSeats {
		i, j := e[0], e[1]
		d[i] |= 1 << (10 - j)
	}
	ans := (n - len(d)) * 2
	masks := [3]int{0b0111100000, 0b0000011110, 0b0001111000}
	for _, x := range d {
		for _, mask := range masks {
			if x&mask == 0 {
				x |= mask
				ans++
			}
		}
	}
	return ans
}

TypeScript

function maxNumberOfFamilies(n: number, reservedSeats: number[][]): number {
    const d: Map<number, number> = new Map();
    for (const [i, j] of reservedSeats) {
        d.set(i, (d.get(i) ?? 0) | (1 << (10 - j)));
    }
    let ans = (n - d.size) << 1;
    const masks = [0b0111100000, 0b0000011110, 0b0001111000];
    for (let [_, x] of d) {
        for (const mask of masks) {
            if ((x & mask) === 0) {
                x |= mask;
                ++ans;
            }
        }
    }
    return ans;
}