| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
Hard |
1697 |
Biweekly Contest 15 Q4 |
|
Given an n x n integer matrix grid, return the minimum sum of a falling path with non-zero shifts.
A falling path with non-zero shifts is a choice of exactly one element from each row of grid such that no two elements chosen in adjacent rows are in the same column.
Example 1:
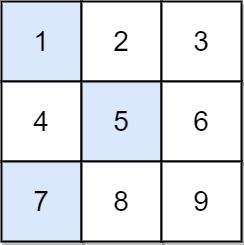
Input: grid = [[1,2,3],[4,5,6],[7,8,9]] Output: 13 Explanation: The possible falling paths are: [1,5,9], [1,5,7], [1,6,7], [1,6,8], [2,4,8], [2,4,9], [2,6,7], [2,6,8], [3,4,8], [3,4,9], [3,5,7], [3,5,9] The falling path with the smallest sum is [1,5,7], so the answer is 13.
Example 2:
Input: grid = [[7]] Output: 7
Constraints:
n == grid.length == grid[i].length1 <= n <= 200-99 <= grid[i][j] <= 99
class Solution:
def minFallingPathSum(self, grid: List[List[int]]) -> int:
n = len(grid)
f = [[0] * n for _ in range(n + 1)]
for i, row in enumerate(grid, 1):
for j, v in enumerate(row):
x = min((f[i - 1][k] for k in range(n) if k != j), default=0)
f[i][j] = v + x
return min(f[n])class Solution {
public int minFallingPathSum(int[][] grid) {
int n = grid.length;
int[][] f = new int[n + 1][n];
final int inf = 1 << 30;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < n; ++j) {
int x = inf;
for (int k = 0; k < n; ++k) {
if (k != j) {
x = Math.min(x, f[i - 1][k]);
}
}
f[i][j] = grid[i - 1][j] + (x == inf ? 0 : x);
}
}
int ans = inf;
for (int x : f[n]) {
ans = Math.min(ans, x);
}
return ans;
}
}class Solution {
public:
int minFallingPathSum(vector<vector<int>>& grid) {
int n = grid.size();
int f[n + 1][n];
memset(f, 0, sizeof(f));
const int inf = 1 << 30;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < n; ++j) {
int x = inf;
for (int k = 0; k < n; ++k) {
if (k != j) {
x = min(x, f[i - 1][k]);
}
}
f[i][j] = grid[i - 1][j] + (x == inf ? 0 : x);
}
}
return *min_element(f[n], f[n] + n);
}
};func minFallingPathSum(grid [][]int) int {
n := len(grid)
f := make([][]int, n+1)
for i := range f {
f[i] = make([]int, n)
}
const inf = 1 << 30
for i, row := range grid {
i++
for j, v := range row {
x := inf
for k := range row {
if k != j {
x = min(x, f[i-1][k])
}
}
if x == inf {
x = 0
}
f[i][j] = v + x
}
}
return slices.Min(f[n])
}class Solution:
def minFallingPathSum(self, grid: List[List[int]]) -> int:
f = g = 0
fp = -1
for row in grid:
ff = gg = inf
ffp = -1
for j, v in enumerate(row):
s = (g if j == fp else f) + v
if s < ff:
gg = ff
ff = s
ffp = j
elif s < gg:
gg = s
f, g, fp = ff, gg, ffp
return fclass Solution {
public int minFallingPathSum(int[][] grid) {
int f = 0, g = 0;
int fp = -1;
final int inf = 1 << 30;
for (int[] row : grid) {
int ff = inf, gg = inf;
int ffp = -1;
for (int j = 0; j < row.length; ++j) {
int s = (j != fp ? f : g) + row[j];
if (s < ff) {
gg = ff;
ff = s;
ffp = j;
} else if (s < gg) {
gg = s;
}
}
f = ff;
g = gg;
fp = ffp;
}
return f;
}
}class Solution {
public:
int minFallingPathSum(vector<vector<int>>& grid) {
int n = grid.size();
int f = 0, g = 0, fp = -1;
const int inf = 1 << 30;
for (auto& row : grid) {
int ff = inf, gg = inf;
int ffp = -1;
for (int j = 0; j < n; ++j) {
int s = (fp != j ? f : g) + row[j];
if (s < ff) {
gg = ff;
ff = s;
ffp = j;
} else if (s < gg) {
gg = s;
}
}
f = ff;
g = gg;
fp = ffp;
}
return f;
}
};func minFallingPathSum(grid [][]int) int {
const inf = 1 << 30
f, g := 0, 0
fp := -1
for _, row := range grid {
ff, gg := inf, inf
ffp := -1
for j, v := range row {
s := f
if j == fp {
s = g
}
s += v
if s < ff {
ff, gg, ffp = s, ff, j
} else if s < gg {
gg = s
}
}
f, g, fp = ff, gg, ffp
}
return f
}