| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
中等 |
|
3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。
给定一个由整数组成的row x col 的 grid,其中有多少个 3 × 3 的 “幻方” 子矩阵?(每个子矩阵都是连续的)。
示例 1:
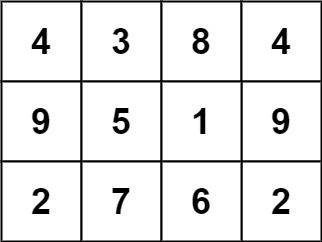
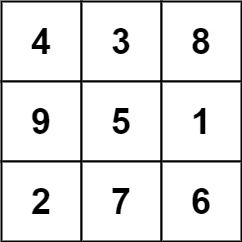
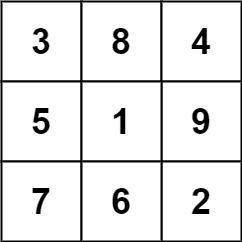
输入: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2] 输出: 1 解释: 下面的子矩阵是一个 3 x 3 的幻方:而这一个不是:
总的来说,在本示例所给定的矩阵中只有一个 3 x 3 的幻方子矩阵。
示例 2:
输入: grid = [[8]] 输出: 0
提示:
row == grid.lengthcol == grid[i].length1 <= row, col <= 100 <= grid[i][j] <= 15
我们直接枚举每个
时间复杂度
class Solution:
def numMagicSquaresInside(self, grid: List[List[int]]) -> int:
def check(i: int, j: int) -> int:
if i + 3 > m or j + 3 > n:
return 0
s = set()
row = [0] * 3
col = [0] * 3
a = b = 0
for x in range(i, i + 3):
for y in range(j, j + 3):
v = grid[x][y]
if v < 1 or v > 9:
return 0
s.add(v)
row[x - i] += v
col[y - j] += v
if x - i == y - j:
a += v
if x - i == 2 - (y - j):
b += v
if len(s) != 9 or a != b:
return 0
if any(x != a for x in row) or any(x != a for x in col):
return 0
return 1
m, n = len(grid), len(grid[0])
return sum(check(i, j) for i in range(m) for j in range(n))class Solution {
private int m;
private int n;
private int[][] grid;
public int numMagicSquaresInside(int[][] grid) {
m = grid.length;
n = grid[0].length;
this.grid = grid;
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
ans += check(i, j);
}
}
return ans;
}
private int check(int i, int j) {
if (i + 3 > m || j + 3 > n) {
return 0;
}
int[] cnt = new int[16];
int[] row = new int[3];
int[] col = new int[3];
int a = 0, b = 0;
for (int x = i; x < i + 3; ++x) {
for (int y = j; y < j + 3; ++y) {
int v = grid[x][y];
if (v < 1 || v > 9 || ++cnt[v] > 1) {
return 0;
}
row[x - i] += v;
col[y - j] += v;
if (x - i == y - j) {
a += v;
}
if (x - i + y - j == 2) {
b += v;
}
}
}
if (a != b) {
return 0;
}
for (int k = 0; k < 3; ++k) {
if (row[k] != a || col[k] != a) {
return 0;
}
}
return 1;
}
}class Solution {
public:
int numMagicSquaresInside(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
int ans = 0;
auto check = [&](int i, int j) {
if (i + 3 > m || j + 3 > n) {
return 0;
}
vector<int> cnt(16);
vector<int> row(3);
vector<int> col(3);
int a = 0, b = 0;
for (int x = i; x < i + 3; ++x) {
for (int y = j; y < j + 3; ++y) {
int v = grid[x][y];
if (v < 1 || v > 9 || ++cnt[v] > 1) {
return 0;
}
row[x - i] += v;
col[y - j] += v;
if (x - i == y - j) {
a += v;
}
if (x - i + y - j == 2) {
b += v;
}
}
}
if (a != b) {
return 0;
}
for (int k = 0; k < 3; ++k) {
if (row[k] != a || col[k] != a) {
return 0;
}
}
return 1;
};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
ans += check(i, j);
}
}
return ans;
}
};func numMagicSquaresInside(grid [][]int) (ans int) {
m, n := len(grid), len(grid[0])
check := func(i, j int) int {
if i+3 > m || j+3 > n {
return 0
}
cnt := [16]int{}
row := [3]int{}
col := [3]int{}
a, b := 0, 0
for x := i; x < i+3; x++ {
for y := j; y < j+3; y++ {
v := grid[x][y]
if v < 1 || v > 9 || cnt[v] > 0 {
return 0
}
cnt[v]++
row[x-i] += v
col[y-j] += v
if x-i == y-j {
a += v
}
if x-i == 2-(y-j) {
b += v
}
}
}
if a != b {
return 0
}
for k := 0; k < 3; k++ {
if row[k] != a || col[k] != a {
return 0
}
}
return 1
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
ans += check(i, j)
}
}
return
}function numMagicSquaresInside(grid: number[][]): number {
const m = grid.length;
const n = grid[0].length;
const check = (i: number, j: number): number => {
if (i + 3 > m || j + 3 > n) {
return 0;
}
const cnt: number[] = new Array(16).fill(0);
const row: number[] = new Array(3).fill(0);
const col: number[] = new Array(3).fill(0);
let [a, b] = [0, 0];
for (let x = i; x < i + 3; ++x) {
for (let y = j; y < j + 3; ++y) {
const v = grid[x][y];
if (v < 1 || v > 9 || ++cnt[v] > 1) {
return 0;
}
row[x - i] += v;
col[y - j] += v;
if (x - i === y - j) {
a += v;
}
if (x - i === 2 - (y - j)) {
b += v;
}
}
}
if (a !== b) {
return 0;
}
for (let k = 0; k < 3; ++k) {
if (row[k] !== a || col[k] !== a) {
return 0;
}
}
return 1;
};
let ans = 0;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
ans += check(i, j);
}
}
return ans;
}