README_EN.md

comments	difficulty	edit_url	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/0600-0699/0690.Employee%20Importance/README_EN.md	Tree Depth-First Search Breadth-First Search Array Hash Table

690. Employee Importance

中文文档

Description

You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.

You are given an array of employees employees where:

• employees[i].id is the ID of the ith employee.
• employees[i].importance is the importance value of the ith employee.
• employees[i].subordinates is a list of the IDs of the direct subordinates of the ith employee.

Given an integer id that represents an employee's ID, return the total importance value of this employee and all their direct and indirect subordinates.

 

Example 1:

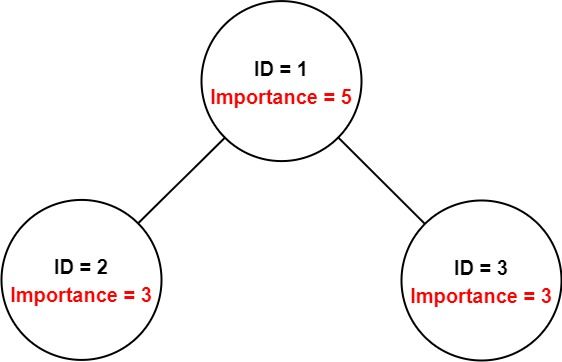
Input: employees = [[1,5,[2,3]],[2,3,[]],[3,3,[]]], id = 1
Output: 11
Explanation: Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.

Example 2:

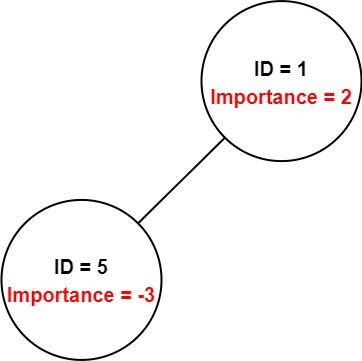
Input: employees = [[1,2,[5]],[5,-3,[]]], id = 5
Output: -3
Explanation: Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.

 

Constraints:

• 1 <= employees.length <= 2000
• 1 <= employees[i].id <= 2000
• All employees[i].id are unique.
• -100 <= employees[i].importance <= 100
• One employee has at most one direct leader and may have several subordinates.
• The IDs in employees[i].subordinates are valid IDs.

Solutions

Solution 1: Hash Table + DFS

We use a hash table $d$ to store all employee information, where the key is the employee's ID, and the value is the employee object. Then we start a depth-first search from the given employee ID. Each time we traverse to an employee, we add the employee's importance to the answer, and recursively traverse all the subordinates of the employee, adding the importance of the subordinates to the answer as well.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of employees.

Python3

"""
# Definition for Employee.
class Employee:
    def __init__(self, id: int, importance: int, subordinates: List[int]):
        self.id = id
        self.importance = importance
        self.subordinates = subordinates
"""


class Solution:
    def getImportance(self, employees: List["Employee"], id: int) -> int:
        def dfs(i: int) -> int:
            return d[i].importance + sum(dfs(j) for j in d[i].subordinates)

        d = {e.id: e for e in employees}
        return dfs(id)

Java

/*
// Definition for Employee.
class Employee {
    public int id;
    public int importance;
    public List<Integer> subordinates;
};
*/

class Solution {
    private final Map<Integer, Employee> d = new HashMap<>();

    public int getImportance(List<Employee> employees, int id) {
        for (var e : employees) {
            d.put(e.id, e);
        }
        return dfs(id);
    }

    private int dfs(int i) {
        Employee e = d.get(i);
        int s = e.importance;
        for (int j : e.subordinates) {
            s += dfs(j);
        }
        return s;
    }
}

C++

/*
// Definition for Employee.
class Employee {
public:
    int id;
    int importance;
    vector<int> subordinates;
};
*/

class Solution {
public:
    int getImportance(vector<Employee*> employees, int id) {
        unordered_map<int, Employee*> d;
        for (auto& e : employees) {
            d[e->id] = e;
        }
        function<int(int)> dfs = [&](int i) -> int {
            int s = d[i]->importance;
            for (int j : d[i]->subordinates) {
                s += dfs(j);
            }
            return s;
        };
        return dfs(id);
    }
};

/**
 * Definition for Employee.
 * type Employee struct {
 *     Id int
 *     Importance int
 *     Subordinates []int
 * }
 */

func getImportance(employees []*Employee, id int) int {
	d := map[int]*Employee{}
	for _, e := range employees {
		d[e.Id] = e
	}
	var dfs func(int) int
	dfs = func(i int) int {
		s := d[i].Importance
		for _, j := range d[i].Subordinates {
			s += dfs(j)
		}
		return s
	}
	return dfs(id)
}

TypeScript

/**
 * Definition for Employee.
 * class Employee {
 *     id: number
 *     importance: number
 *     subordinates: number[]
 *     constructor(id: number, importance: number, subordinates: number[]) {
 *         this.id = (id === undefined) ? 0 : id;
 *         this.importance = (importance === undefined) ? 0 : importance;
 *         this.subordinates = (subordinates === undefined) ? [] : subordinates;
 *     }
 * }
 */

function getImportance(employees: Employee[], id: number): number {
    const d = new Map<number, Employee>();
    for (const e of employees) {
        d.set(e.id, e);
    }
    const dfs = (i: number): number => {
        let s = d.get(i)!.importance;
        for (const j of d.get(i)!.subordinates) {
            s += dfs(j);
        }
        return s;
    };
    return dfs(id);
}

JavaScript

/**
 * Definition for Employee.
 * function Employee(id, importance, subordinates) {
 *     this.id = id;
 *     this.importance = importance;
 *     this.subordinates = subordinates;
 * }
 */

/**
 * @param {Employee[]} employees
 * @param {number} id
 * @return {number}
 */
var GetImportance = function (employees, id) {
    const d = new Map();
    for (const e of employees) {
        d.set(e.id, e);
    }
    const dfs = i => {
        let s = d.get(i).importance;
        for (const j of d.get(i).subordinates) {
            s += dfs(j);
        }
        return s;
    };
    return dfs(id);
};