README.md

comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0400-0499/0469.Convex%20Polygon/README.md	几何 数组 数学

469. 凸多边形 🔒

English Version

题目描述

给定 X-Y 平面上的一组点 points ，其中 points[i] = [xi, yi] 。这些点按顺序连成一个多边形。

如果该多边形为 凸 多边形（凸多边形的定义）则返回 true ，否则返回 false 。

你可以假设由给定点构成的多边形总是一个 简单的多边形（简单多边形的定义）。换句话说，我们要保证每个顶点处恰好是两条边的汇合点，并且这些边 互不相交 。

 

示例 1：

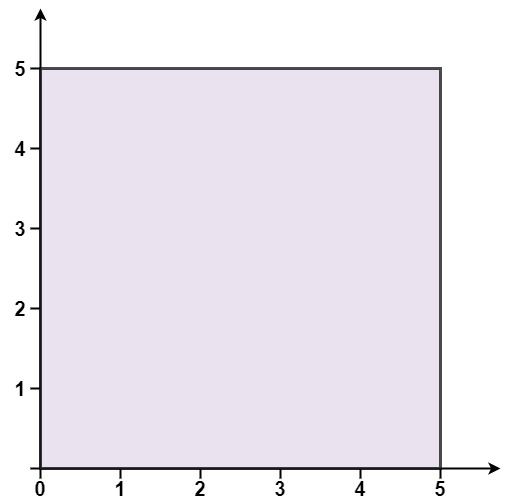
输入: points = [[0,0],[0,5],[5,5],[5,0]]
输出: true

示例 2：

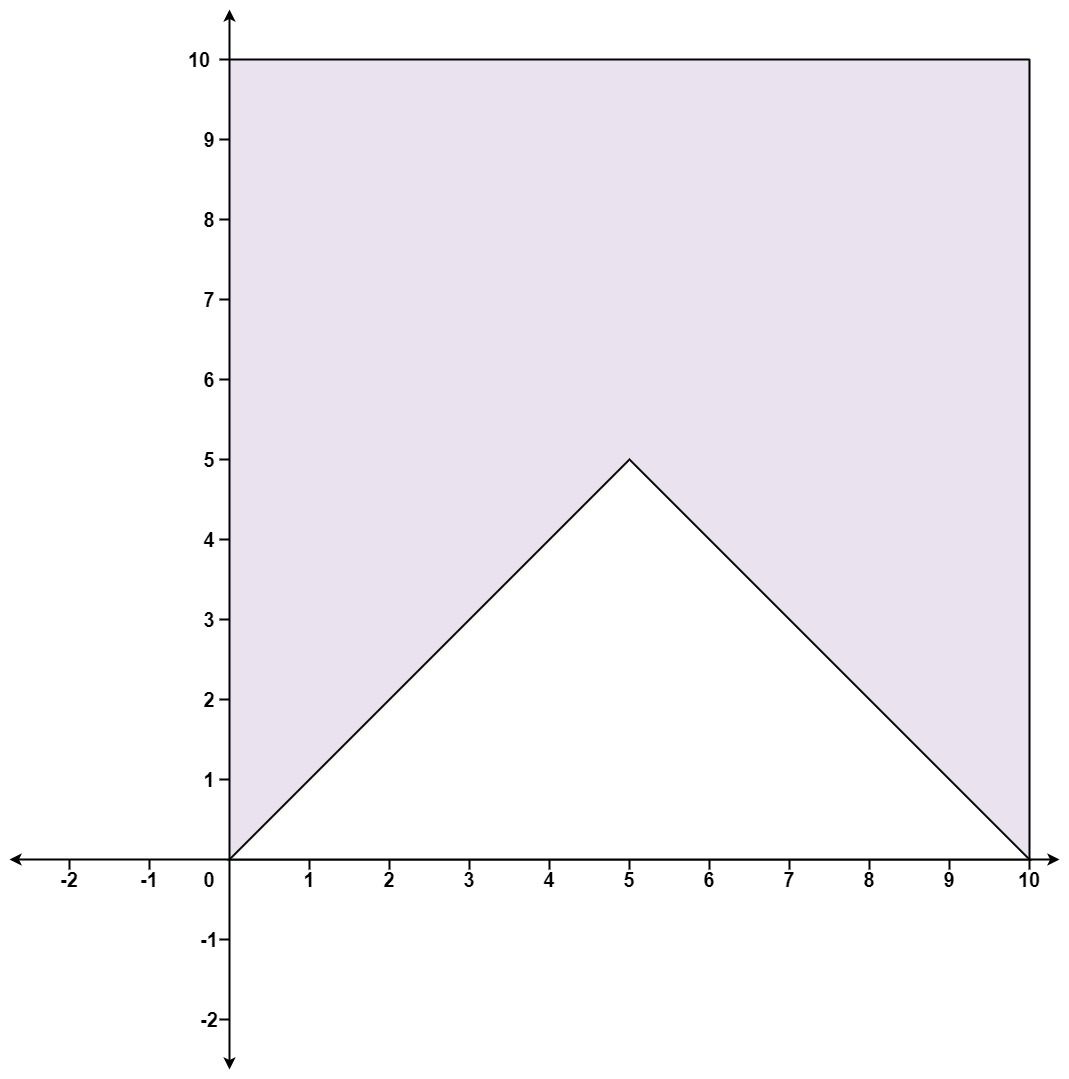
输入: points = [[0,0],[0,10],[10,10],[10,0],[5,5]]
输出: false

 

提示:

• 3 <= points.length <= 104
• points[i].length == 2
• -104 <= xi, yi <= 104
• 所有点都 不同

 

解法

方法一：数学（向量叉积）

假设当前连续的三个顶点分别为 $p_1, p_2, p_3$，我们可以计算向量 $\overrightarrow{p_1p_2}$ 和 $\overrightarrow{p_1p_3}$ 的叉积，记为 $cur$。如果 $cur$ 的方向与之前的 $pre$ 方向不一致，说明多边形不是凸多边形 🔒。否则，我们更新 $pre = cur$，继续遍历下一个顶点。

遍历结束，如果没有发现不一致的情况，说明多边形是凸多边形 🔒。

时间复杂度 $O(n)$，其中 $n$ 是顶点的数量。空间复杂度 $O(1)$。

Python3

class Solution:
    def isConvex(self, points: List[List[int]]) -> bool:
        n = len(points)
        pre = cur = 0
        for i in range(n):
            x1 = points[(i + 1) % n][0] - points[i][0]
            y1 = points[(i + 1) % n][1] - points[i][1]
            x2 = points[(i + 2) % n][0] - points[i][0]
            y2 = points[(i + 2) % n][1] - points[i][1]
            cur = x1 * y2 - x2 * y1
            if cur != 0:
                if cur * pre < 0:
                    return False
                pre = cur
        return True

Java

class Solution {
    public boolean isConvex(List<List<Integer>> points) {
        int n = points.size();
        long pre = 0, cur = 0;
        for (int i = 0; i < n; ++i) {
            var p1 = points.get(i);
            var p2 = points.get((i + 1) % n);
            var p3 = points.get((i + 2) % n);
            int x1 = p2.get(0) - p1.get(0);
            int y1 = p2.get(1) - p1.get(1);
            int x2 = p3.get(0) - p1.get(0);
            int y2 = p3.get(1) - p1.get(1);
            cur = x1 * y2 - x2 * y1;
            if (cur != 0) {
                if (cur * pre < 0) {
                    return false;
                }
                pre = cur;
            }
        }
        return true;
    }
}

C++

class Solution {
public:
    bool isConvex(vector<vector<int>>& points) {
        int n = points.size();
        long long pre = 0, cur = 0;
        for (int i = 0; i < n; ++i) {
            int x1 = points[(i + 1) % n][0] - points[i][0];
            int y1 = points[(i + 1) % n][1] - points[i][1];
            int x2 = points[(i + 2) % n][0] - points[i][0];
            int y2 = points[(i + 2) % n][1] - points[i][1];
            cur = 1L * x1 * y2 - x2 * y1;
            if (cur != 0) {
                if (cur * pre < 0) {
                    return false;
                }
                pre = cur;
            }
        }
        return true;
    }
};

Go

func isConvex(points [][]int) bool {
	n := len(points)
	pre, cur := 0, 0
	for i := range points {
		x1 := points[(i+1)%n][0] - points[i][0]
		y1 := points[(i+1)%n][1] - points[i][1]
		x2 := points[(i+2)%n][0] - points[i][0]
		y2 := points[(i+2)%n][1] - points[i][1]
		cur = x1*y2 - x2*y1
		if cur != 0 {
			if cur*pre < 0 {
				return false
			}
			pre = cur
		}
	}
	return true
}