README_EN.md

comments	difficulty	edit_url	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/0200-0299/0221.Maximal%20Square/README_EN.md	Array Dynamic Programming Matrix

221. Maximal Square

中文文档

Description

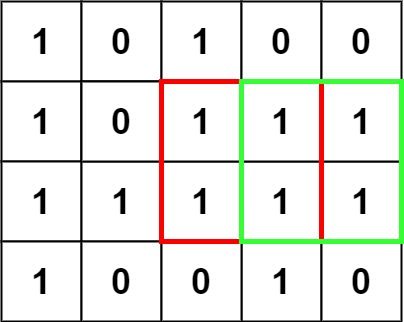
Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

 

Example 1:

Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:

Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] is '0' or '1'.

Solutions

Solution 1: Dynamic Programming

We define $dp[i + 1][j + 1]$ as the maximum square side length with the lower right corner at index $(i, j)$. The answer is the maximum value among all $dp[i + 1][j + 1]$.

The state transition equation is:

$$ dp[i + 1][j + 1] = \begin{cases} 0 & \text{if } matrix[i][j] = '0' \\ \min(dp[i][j], dp[i][j + 1], dp[i + 1][j]) + 1 & \text{if } matrix[i][j] = '1' \end{cases} $$

The time complexity is $O(m\times n)$, and the space complexity is $O(m\times n)$. Where $m$ and $n$ are the number of rows and columns of the matrix, respectively.

Python3

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m, n = len(matrix), len(matrix[0])
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        mx = 0
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == '1':
                    dp[i + 1][j + 1] = min(dp[i][j + 1], dp[i + 1][j], dp[i][j]) + 1
                    mx = max(mx, dp[i + 1][j + 1])
        return mx * mx

Java

class Solution {
    public int maximalSquare(char[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        int[][] dp = new int[m + 1][n + 1];
        int mx = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == '1') {
                    dp[i + 1][j + 1] = Math.min(Math.min(dp[i][j + 1], dp[i + 1][j]), dp[i][j]) + 1;
                    mx = Math.max(mx, dp[i + 1][j + 1]);
                }
            }
        }
        return mx * mx;
    }
}

C++

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        int mx = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == '1') {
                    dp[i + 1][j + 1] = min(min(dp[i][j + 1], dp[i + 1][j]), dp[i][j]) + 1;
                    mx = max(mx, dp[i + 1][j + 1]);
                }
            }
        }
        return mx * mx;
    }
};

Go

func maximalSquare(matrix [][]byte) int {
	m, n := len(matrix), len(matrix[0])
	dp := make([][]int, m+1)
	for i := 0; i <= m; i++ {
		dp[i] = make([]int, n+1)
	}
	mx := 0
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if matrix[i][j] == '1' {
				dp[i+1][j+1] = min(min(dp[i][j+1], dp[i+1][j]), dp[i][j]) + 1
				mx = max(mx, dp[i+1][j+1])
			}
		}
	}
	return mx * mx
}

C#

public class Solution {
    public int MaximalSquare(char[][] matrix) {
        int m = matrix.Length, n = matrix[0].Length;
        var dp = new int[m + 1, n + 1];
        int mx = 0;
        for (int i = 0; i < m; ++i)
        {
            for (int j = 0; j < n; ++j)
            {
                if (matrix[i][j] == '1')
                {
                    dp[i + 1, j + 1] = Math.Min(Math.Min(dp[i, j + 1], dp[i + 1, j]), dp[i, j]) + 1;
                    mx = Math.Max(mx, dp[i + 1, j + 1]);
                }
            }
        }
        return mx * mx;
    }
}