Skip to content

Latest commit

 

History

History
274 lines (227 loc) · 5.82 KB

README.md

File metadata and controls

274 lines (227 loc) · 5.82 KB
Raw
comments difficulty edit_url tags
true
简单
树
深度优先搜索
广度优先搜索
二叉树

104. 二叉树的最大深度

English Version

题目描述

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

 

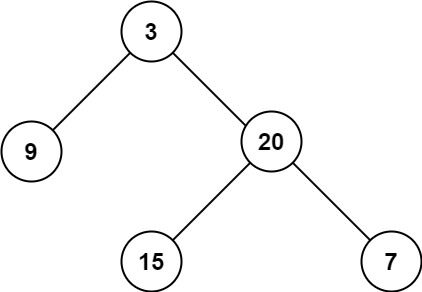
示例 1：

 

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

 

提示：

  • 树中节点的数量在 [0, 104] 区间内。
  • -100 <= Node.val <= 100

解法

方法一：递归

递归遍历左右子树，求左右子树的最大深度，然后取最大值加 $1$ 即可。

时间复杂度 $O(n)$，其中 $n$ 是二叉树的节点数。每个节点在递归中只被遍历一次。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        l, r = self.maxDepth(root.left), self.maxDepth(root.right)
        return 1 + max(l, r)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int l = maxDepth(root.left);
        int r = maxDepth(root.right);
        return 1 + Math.max(l, r);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (!root) return 0;
        int l = maxDepth(root->left), r = maxDepth(root->right);
        return 1 + max(l, r);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
	if root == nil {
		return 0
	}
	l, r := maxDepth(root.Left), maxDepth(root.Right)
	return 1 + max(l, r)
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function maxDepth(root: TreeNode | null): number {
    if (root === null) {
        return 0;
    }
    return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    fn dfs(root: &Option<Rc<RefCell<TreeNode>>>) -> i32 {
        if root.is_none() {
            return 0;
        }
        let node = root.as_ref().unwrap().borrow();
        1 + Self::dfs(&node.left).max(Self::dfs(&node.right))
    }

    pub fn max_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        Self::dfs(&root)
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function (root) {
    if (!root) return 0;
    const l = maxDepth(root.left);
    const r = maxDepth(root.right);
    return 1 + Math.max(l, r);
};

C

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

#define max(a, b) (((a) > (b)) ? (a) : (b))

int maxDepth(struct TreeNode* root) {
    if (!root) {
        return 0;
    }
    int left = maxDepth(root->left);
    int right = maxDepth(root->right);
    return 1 + max(left, right);
}