队列是限定在一端进行插入,另一端进行删除特殊线性表。
就像排队买东西,排在前面的人买完东西后离开队伍(删除),而后来的人总是排在队伍未尾(插入)。
通常把队列的删除和插入分别称为出队和入队。允许出队的一端称为队头,允许入队的一端称为队尾。所有需要进队的数据项,只能从队尾进入,队列中的数据项只能从队头离去。由于总是先入队的元素先出队(先排队的人先买完东西),这种表也称为先进先出(FIFO)表。
队列可以用数组Q[m+1]来存储,数组的上界m即是队列所容许的最大容量。在队列的运算中需设两个指针:
head:队头指针,指向实际队头元素的前一个位置
tail:队尾指针,指向实际队尾元素所在的位置
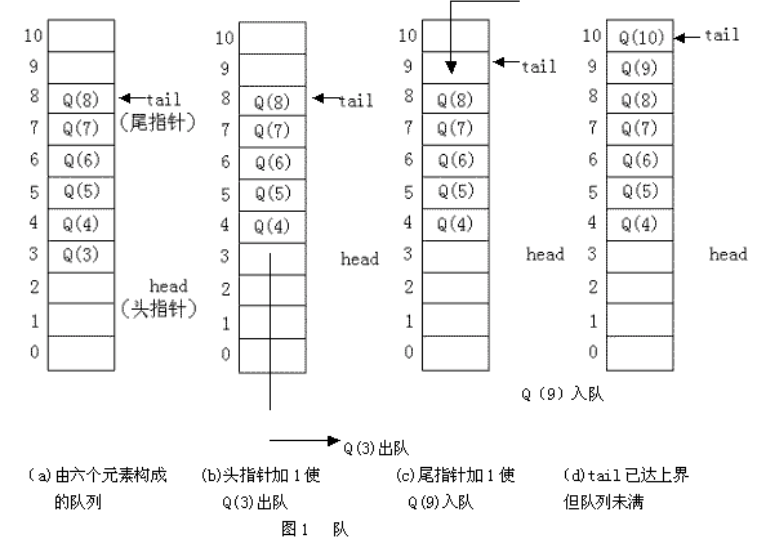
一般情况下,两个指针的初值设为0,这时队列为空,没有元素。图1 (a)画出了一个由6个元素构成的队列,数组定义Q[11]。
Q[i] i=3,4,5,6,7,8 头指针head=2,尾指针tail=8。
队列中拥有的元素个数为:L=tail-head现要让排头的元素出队,则需将头指针加1。即head=head+1这时头指针向上移动一个位置,指向Q[3],表示Q[3]已出队。见图1 (b)。
如果想让一个新元素入队,则需尾指针向上移动一个位置。即tail=tail+1这时Q[9]入队,见图1 (c)。
当队尾已经处理在最上面时,即tail=10,见图1 (d),如果还要执行入队操作,则要发生“上溢”,但实际上队列中还有三个空位置,所以这种溢出称为“假溢出”。
克服假溢出的方法有两种。
一种是将队列中的所有元素均向低地址区移动,显然这种方法是很浪费时间的;
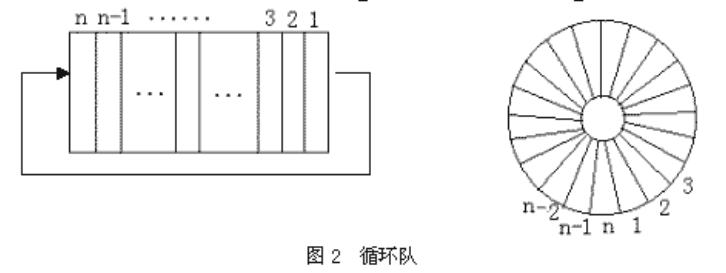
另一种方法是将数组存储区看成是一个首尾相接的环形区域。当存放到n地址后,下一个地址就"翻转"为1。
在结构上采用这种技巧来存储的队列称为循环队列,见图2
循环队的入队算法如下:
1、tail=tail+1;
2、若tail=n+1,则tail=1;
3、若head=tail尾指针与头指针重合了,表示元素已装满队列, 则作上溢出错处理;�
4、否则,Q[tail]=x,结束(x为新入出元素)。
队列和栈一样,有着非常广泛的应用。
考虑一个分时系统,如果一台计算机联有四个终端,即允许四个用户同时使用这一台计算机。
那么,计算机系统必须设立一个队列, 用以管理各终端用户使用CPU的请求。
当某个用户要求使用CPU时,相应的终端代号就入队(插入队尾),而队头的终端用户则是CPU当前服务的对象。
我们考虑最简单的情况, 对于当前用户(队头),系统每次分配一个为时间片的时间间隔,在一个时间片内,如果当前用户的作业没有结束,则该终端用户的代号出队后重新入队,插入队尾,等待下一次CPU服务。
如果某个用户的作业运行结束,则先退出,出队后不再入队,整个运行过程就是各终端代号不断地入队、出队,CPU 轮流地为n(n≤4)个终端用户服务。
由于计算机的运行速度极快,所以,对于每个终端用户来说,似乎计算机是单独在为其服务。
和线性表一样,栈和队可以采用链表存储结构,当要实现多个栈共享内存或多个队共享内存时,选择链式分配结构则更为合适。
【例1】假设在周末舞会上,男士们和女士们进入舞厅时,各自排成一队。跳舞开始时,依次从男队和女队的队头上各出一人配成舞伴。规定每个舞曲能有一对跳舞者。若两队初始人数不相同,则较长的那一队中未配对者等待下一轮舞曲。现要求写一个程序,模拟上述舞伴配对问题。
输入:
第一行两队的人数
第二行舞曲的数目
【分析】:设计两个队列分别存放男士和女士。每对跳舞的人一旦跳完后就回到队尾等待下次被选。如m=4 n=3 k=6
【参考程序】
#include<cstdio>
#include<iostream>
using namespace std;
int a[10001],b[10001],k1=1,k,i,f1=1,r1,f2=1,r2;
main()
{
int m,n;
cin>>m>>n;
for (i=1;i<=m;i++) a[i]=i;
for (i=1;i<=n;i++) b[i]=i;
cin>>k;
r1=m; r2=n;
while (k1<=k)
{
printf("%d %d\n",a[f1],b[f2]);
r1++; a[r1]=a[f1]; f1++; //第一次a[m+1]=a[1]=1,第二次a[m+2]=a[2]=2,如此循环
r2++; b[r2]=b[f2]; f2++; //第一次b[n+1]=b[1]=1,第二次b[n+2]=b[2]=2,如此循环。
k1++;
}
return 0;
} 【例2】集合的前N个元素:编一个程序,按递增次序生成集合M的最小的N个数,M的定义如下:
(1)数1属于M;
(2)如果X属于M,则Y=2x+1和Z=3x+1也属于M;
(3)此外再没有别的数属于M。
【分析】
可以用两个队列a和b来存放新产生的数,然后通过比较大小决定是否输出,具体方法如下:
(1)令fa和fb分别为队列a和队列b的头指针,它们的尾指针分别为ra和rb。
初始时,X=1,fa=fb=ra=rb=1;
(2)将2x+1和3x+1分别放入队列a和队列b的队尾,尾指针加1。
即:a[r]←2x+1,b[r]←3x+1,r←r+1;
(3)将队列a和队列b的头结点进行比较,可能有三种情况:(A)a[ha]>b[hb] (B)a[ha]=b[hb] (C)a[ha]<b[hb]
将比较的小者取出送入X,取出数的队列的头指针相应加1。
(4)重复(2),(3)直至取出第N项为止。
【参考程序】
#include<cstdio>
using namespace std;
int a[1001],b[1001],x=1,fa=1,fb=1,ra=0,rb=0,total=1,n,i;
main()
{
printf("N="); scanf("%d",&n);
while (total<=n)
{
printf("%d ",x);
a[++ra]=2*x+1;
b[++rb]=3*x+1;
if (a[fa]>b[fb]) x=b[fb++];
else if (a[fa]<b[fb]) x=a[fa++];
else
{
x=a[fa++];
fb++;
}
total++;
}
return 0;
}【例3】设有n个人依次围成一圈,从第1个人开始报数,数到第m个人出列,然后从出列的下一个人开始报数,数到第m个人又出列,…,如此反复到所有的人全部出列为止。设n个人的编号分别为1,2,…,n,打印出列的顺序。
【算法分析】
本题我们可以用数组建立标志位等方法求解,但如果用上数据结构中循环链的思想,则更贴切题意,解题效率更高。n人围成一圈,把一人看成一个结点,n人之间的关系采用链接方式,即每一结点有一个前继结点和一个后继结点,每一个结点有一个指针指向下一个结点,最后一个结点指针指向第一个结点。这就是单循环链的数据结构。当m人出列时,将m结点的前继结点指针指向m结点的后继结点指针,即把m结点驱出循环链。
1、建立循环链表。
当用数组实现本题链式结构时,数组a[i]作为"指针"变量来使用,a[i]存放下一个结点的位置。设立指针j指向当前结点,则移动结点过程为j=a[j],当数到m时,m结点出链,则a[j]=a[a[j]]。 当直接用链来实现时,则比较直观,每个结点有两个域:一个数值域,一个指针域,当数到m时,m出链,将m结点的前继结点指针指向其后继结点;
2、设立指针,指向当前结点,设立计数器,计数数到多少人;
3、沿链移动指针,每移动一个结点,计数器值加1,当计数器值为m时, 则m结点出链,计数器值置为1。
4、重复3,直到n个结点均出链为止。
【参考程序】用数组实现链式结构
#include<cstdio>
using namespace std;
const int n=10,m=4; //设有10个人,报到4的人出列
int a[n+1],j=n,k=1,p=0;
main()
{
for (int i=1;i<n;i++) a[i]=i+1; //建立链表
a[n]=1; //第n人指向第1人,形成一个环
while (p<n) //n个人均出队为止
{
while(k<m) //报数,计数器加1
{
j=a[j];
k++;
}
printf("%d ",a[j]); p++; //数到m,此人出队,计数器置1
a[j]=a[a[j]]; k=1;
}
return 0;
}【例4】一矩形阵列由数字0到9组成,数字1到9代表细胞,细胞的定义为沿细胞数字上下左右还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数。如:
阵列 4 10
0234500067
1034560500
2045600671
0000000089
有4个细胞。
【算法分析】
- 从文件中读入m*n矩阵阵列,将其转换为bool矩阵存入b数组中;�
- 沿b数组矩阵从上到下,从左到右,找到遇到的第一个细胞;�
- 将细胞的位置入队h,并沿其上、下、左、右四个方向上的细胞位置入队,入队后的位置b数组置为flase;
- 将h队的队头出队,沿其上、下、左、右四个方向上的细胞位置入队,入队后的位置b数组置为flase;�
- 重复4,直至h队空为止,则此时找出了一个细胞;�
- 重复2,直至矩阵找不到细胞;�
- 输出找到的细胞数。
#include<cstdio>
using namespace std;
char a[51][51];
bool b[51][51];
int n,m,i,j,s=0,c[5]={1,0,-1,0,1};
void f(int,int);
main()
{
scanf("%d%d\n",&n,&m);
for (i=0;i<n;i++)
gets(a[i]);
for (i=0;i<n;i++)
for (j=0;j<m;j++)
b[i][j]=a[i][j]-'0';
for (i=0;i<n;i++) //在矩阵中寻找细胞
for (j=0;j<m;j++)
if (b[i][j])
{
b[i][j]=0;
f(i,j);
s++;
}
printf("%d",s);
return 0;
}
void f(int x,int y)
{
for (int i=0;i<=4;i++)
if (x+c[i]>-1&&x+c[i]<n&&y+c[i+1]>-1&&y+c[i+1]<m&&b[x+c[i]][y+c[i+1]])
{ //沿细胞的上下左右四个方向搜索细胞
b[x+c[i]][y+c[i+1]]=0;
f(x+c[i],y+c[i+1]);
}
}【例2-5】最少步数
【问题描述】
在各种棋中,棋子的走法总是一定的,如中国象棋中马走“日”。有一位小学生就想如果马能有两种走法将增加其趣味性,因此,他规定马既能按“日”走,也能如象一样走“田”字。他的同桌平时喜欢下围棋,知道这件事后觉得很有趣,就想试一试,在一个(100*100)的围棋盘上任选两点A、B,A点放上黑子,B点放上白子,代表两匹马。棋子可以按“日”字走,也可以按“田”字走,俩人一个走黑马,一个走白马。谁用最少的步数走到左上角坐标为(1,1)的点时,谁获胜。现在他请你帮忙,给你A、B两点的坐标,想知道两个位置到(1,1)点可能的最少步数。�
【输入样例】
12 16�
18 10�
【输出样例】
8� 9
【算法分析】 由于A、B两点是随机输入的,因此无法找到计算最少步数的数学规律,只能通过广度优先搜索的办法求解。
- 确定出发点 从(x,y)出发通过一次广度优先搜索,可以找到从(x,y)至棋盘上所有可达点的最少步数。而问题中要求的是黑马所在的(x1,y1)和白马所在(x2,y2)到达 (1,1) 目标点的最少步数。虽然两条路径的起点不一样,但是它们的终点却是一样的。如果我们将终点(1,1)作为起点,这样只需要一次广度优先搜索便可以得到(x1,y1)和(x2,y2)到达(1,1)的最少步数。
- 数据结构
设queue——队列,存储从(1,1)可达的点(
queue[k][1..2])以及到达该点所需要的最少步数(queue[k][3])(0≤k≤192+1)。队列的首指针为open,尾指针为closed。初始时,queue中只有一个元素为(1,1),最少步数为0。- S——记录(1,1)到每点所需要的最少步数。显然,问题的答案是
s[x1][y1]和s[x2][y2]。初始时,s[1][1]为0,除此之外的所有元素值设为-1。 - dx、dy——移动后的位置增量数组。马有12种不同的扩展方向:
马走“日”:
(x-2,y-1)(x-1,y-2)(x-2,y+1)(x-1,y+2)(x+2,y-1)(x+1,y-2)(x+2,y+1)(x+1,y+2)马走“田”:(x-2,y-2)(x-2,y+2)(x+2,y-2)(x+2,y+2) - 我们将i方向上的位置增量存入常量数组
dx[i]、dy[i]中(0≤i≤11)int dx[12]={-2,-2,-1,1,2,2,2,2,1,-1,-2,-2},dy[12]={-1,-2,-2,-2,-2,-1,1,2,2,2,2,1};
- S——记录(1,1)到每点所需要的最少步数。显然,问题的答案是
- 约束条件
- 不能越出界外。由于马的所有可能的落脚点s均在s的范围内,因此一旦马越出界外,就将其s值赋为0,表示“已经扩展过,且(1,1)到达其最少需要0步”。这看上去是荒谬的,但可以简单而有效地避免马再次落入这些界外点。
- 该点在以前的扩展中没有到达过。如果曾经到达过,则根据广度优先搜索的原理,先前到达该点所需的步数一定小于当前步数,因此完全没有必要再扩展下去。
由此得出,马的跳后位置(x,y)是否可以入队的约束条件是
s[x][y]<0
4、算法流程
#include <cstdlib>
#include <cstring>
#include <iostream>
using namespace std;
int dx[12]={-2,-2,-1,1,2,2,2,2,1,-1,-2,-2},
dy[12]={-1,-2,-2,-2,-2,-1,1,2,2,2,2,1};
int main()
{
int s[101][101],que[10000][4]={0},x1,y1,x2,y2;
memset(s,0xff,sizeof(s)); //s数组的初始化
int head=1,tail=1; //初始位置入队
que[1][1]=1;que[1][2]=1;que[1][3]=0;
cin>>x1>>y1>>x2>>y2; //读入黑马和白马的出发位置
while(head<=tail) //若队列非空,则扩展队首结点
{
for(int d=0;d<=11;d++) //枚举12个扩展方向
{
int x=que[head][1]+dx[d]; //计算马按d方向跳跃后的位置
int y=que[head][2]+dy[d];
if(x>0&&y>0)
if(s[x][y]==-1) //若(x,y)满足约束条件
{
s[x][y]=que[head][3]+1; //计算(1,1)到(x,y)的最少步数
tail++; //(1,1)至(x,y)的最少步数入队
que[tail][1]=x;
que[tail][2]=y;
que[tail][3]=s[x][y];
if(s[x1][y1]>0&&s[x2][y2]>0) //输出问题的解
{
cout<<s[x1][y1]<<endl;
cout<<s[x2][y2]<<endl;
system("pause");
return 0;
}
}
}
head++;
}
}