搜索与回溯是计算机解题中常用的算法,很多问题无法根据某种确定的计算法则来求解,可以利用搜索与回溯的技术求解。回溯是搜索算法中的一种控制策略。它的基本思想是:为了求得问题的解,先选择某一种可能情况向前探索,在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索,如此反复进行,直至得到解或证明无解。
如迷宫问题:进入迷宫后,先随意选择一个前进方向,一步步向前试探前进,如果碰到死胡同,说明前进方向已无路可走,这时,首先看其它方向是否还有路可走,如果有路可走,则沿该方向再向前试探;如果已无路可走,则返回一步,再看其它方向是否还有路可走;如果有路可走,则沿该方向再向前试探。按此原则不断搜索回溯再搜索,直到找到新的出路或从原路返回入口处无解为止。
递归回溯法算法框架[一]
int Search(int k)
{
for (i=1;i<=算符种数;i++)
if (满足条件)
{
保存结果
if (到目的地) 输出解;
else Search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}递归回溯法算法框架[二]
int Search(int k)
{
if (到目的地) 输出解;
else
for (i=1;i<=算符种数;i++)
if (满足条件)
{
保存结果;
Search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}【例1】素数环:从1到20这20个数摆成一个环,要求相邻的两个数的和是一个素数。
【算法分析】
非常明显,这是一道回溯的题目。从1开始,每个空位有20种可能,只要填进去的数合法:与前面的数不相同;与左边相邻的数的和是一个素数。第20个数还要判断和第1个数的和是否素数。
【算法流程】
1、数据初始化; 2、递归填数:判断第i个数填入是否合法;
A、如果合法:填数;判断是否到达目标(20个已填完):是,打印结果;不是,递归填下一个;
B、如果不合法:选择下一种可能;
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cmath>
using namespace std;
bool b[21]={0};
int total=0,a[21]={0};
int search(int); //回溯过程
int print(); //输出方案
bool pd(int,int); //判断素数
int main()
{
search(1);
cout<<total<<endl; //输出总方案数
system("pause");
}
int search(int t)
{
int i;
for (i=1;i<=20;i++) //有20个数可选
if (pd(a[t-1],i)&&(!b[i])) //判断与前一个数是否构成素数及该数是否可用
{
a[t]=i;
b[i]=1;
if (t==20) { if (pd(a[20],a[1])) print();}
else search(t+1);
b[i]=0;
}
}
int print()
{
total++;
cout<<"<"<<total<<">";
for (int j=1;j<=20;j++)
cout<<a[j]<<" ";
cout<<endl;
}
bool pd(int x,int y)
{
int k=2,i=x+y;
while (k<=sqrt(i)&&i%k!=0) k++;
if (k>sqrt(i)) return 1;
else return 0;
}【例2】设有n个整数的集合{1,2,…,n},从中取出任意r个数进行排列(r<n),试列出所有的排列。
#include<cstdio>
#include<iostream>
#include<iomanip>
using namespace std;
int num=0,a[10001]={0},n,r;
bool b[10001]={0};
int search(int); //回溯过程
int print(); //输出方案
int main()
{
cout<<"input n,r:";
cin>>n>>r;
search(1);
cout<<"number="<<num<<endl; //输出方案总数
}
int search(int k)
{
int i;
for (i=1;i<=n;i++)
if (!b[i]) //判断i是否可用
{
a[k]=i; //保存结果
b[i]=1;
if (k==r) print();
else search(k+1);
b[i]=0;
}
}
int print()
{
num++;
for (int i=1;i<=r;i++)
cout<<setw(3)<<a[i];
cout<<endl;
}【例3】任何一个大于1的自然数n,总可以拆分成若干个小于n的自然数之和。
当n=7共14种拆分方法:
7=1+1+1+1+1+1+1
7=1+1+1+1+1+2
7=1+1+1+1+3
7=1+1+1+2+2
7=1+1+1+4
7=1+1+2+3
7=1+1+5
7=1+2+2+2
7=1+2+4
7=1+3+3
7=1+6
7=2+2+3
7=2+5
7=3+4
total=14
#include<cstdio>
#include<iostream>
#include<cstdlib>
using namespace std;
int a[10001]={1},n,total;
int search(int,int);
int print(int);
int main()
{
cin>>n;
search(n,1);
//将要拆分的数n传递给s
cout<<"total="<<total<<endl; //输出拆分的方案数
system("pause");
}
int search(int s,int t)
{
int i;
for (i=a[t-1];i<=s;i++)
if (i<n)
//当前数i要大于等于前1位数,且不过n
{
a[t]=i;
//保存当前拆分的数i
s-=i;
//s减去数i, s的值将继续拆分
if (s==0) print(t);
//当s=0时,拆分结束输出结果
else search(s,t+1);
//当s>0时,继续递归
s+=i;
//回溯:加上拆分的数,以便产分所有可能的拆分
}
}
int print(int t)
{
cout<<n<<"=";
for (int i=1;i<=t-1;i++)
//输出一种拆分方案
cout<<a[i]<<"+";
cout<<a[t]<<endl;
total++;
//方案数累加1
}【例4】八皇后问题:要在国际象棋棋盘中放八个皇后,使任意两个皇后都不能互相吃。(提示:皇后能吃同一行、同一列、同一对角线的任意棋子。)
放置第i个(行)皇后的算法为:
int search(i);
{
int j;
for (第i个皇后的位置j=1;j<=8;j++ ) //在本行的8列中去试
if (本行本列允许放置皇后)
{
放置第i个皇后;
对放置皇后的位置进行标记;
if (i==8) 输出 //已经放完个皇后
else search(i+1); //放置第i+1个皇后
对放置皇后的位置释放标记,尝试下一个位置是否可行;
}
}【算法分析】
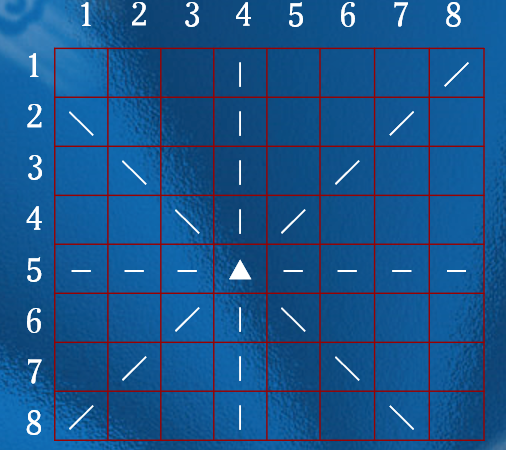
显然问题的关键在于如何判定某个皇后所在的行、列、斜线上是否有别的皇后;可以从矩阵的特点上找到规律,如果在同一行,则行号相同;如果在同一列上,则列号相同;如果同在/ 斜线上的行列值之和相同;如果同在\ 斜线上的行列值之差相同;从下图可验证:
考虑每行有且仅有一个皇后,设一维数组A[1..8]表示皇后的放置:第i行皇后放在第j列,用A[i]=j来表示,即下标是行数,内容是列数。例如:A[3]=5就表示第3个皇后在第3行第5列上。
判断皇后是否安全,即检查同一列、同一对角线是否已有皇后,建立标志数组b[1..8]控制同一列只能有一个皇后,若两皇后在同一对角线上,则其行列坐标之和或行列坐标之差相等,故亦可建立标志数组c[1..16]、d[-7..7]控制同一对角线上只能有一个皇后。
如果斜线不分方向,则同一斜线上两皇后的行号之差的绝对值与列号之差的绝对值相同。在这种方式下,要表示两个皇后I和J不在同一列或斜线上的条件可以描述为:A[I]<>A[J] AND ABS(I-J)<>ABS(A[I]-A[J]){I和J分别表示两个皇后的行号}
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<iomanip>
using namespace std;
bool d[100]={0},b[100]={0},c[100]={0};
int sum=0,a[100];
int search(int);
int print();
int main()
{
search(1); //从第1个皇后开始放置
system("pause");
}
int search(int i)
{
int j;
for (j=1;j<=8;j++) //每个皇后都有8位置(列)可以试放
if ((!b[j])&&(!c[i+j])&&(!d[i-j+7])) //寻找放置皇后的位置
//由于C++不能操作负数组,因此考虑加7
{ //放置皇后,建立相应标志值
a[i]=j; //摆放皇后
b[j]=1; //宣布占领第j列
c[i+j]=1; //占领两个对角线
d[i-j+7]=1;
if (i==8) print(); //8个皇后都放置好,输出
else search(i+1); //继续递归放置下一个皇后
b[j]=0; //递归返回即为回溯一步,当前皇后退出
c[i+j]=0;
d[i-j+7]=0;
}
}
int print()
{
int i;
sum++; //方案数累加1
cout<<"sum="<<sum<<endl;
for (i=1;i<=8;i++) //输出一种方案
cout<<setw(4)<<a[i];
cout<<endl;
}【例5】马的遍历
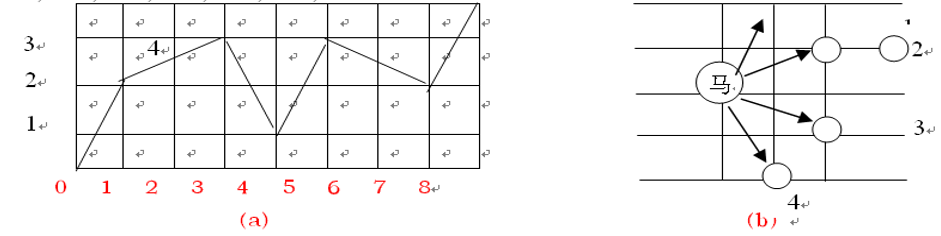
中国象棋半张棋盘如图4(a)所示。马自左下角往右上角跳。今规定只许往右跳,不许往左跳。比如图4(a)中所示为一种跳行路线,并将所经路线打印出来。打印格式为:0,0->2,1->3,3->1,4->3,5->2,7->4,8…
【算法分析】
如图4(b),马最多有四个方向,若原来的横坐标为j、纵坐标为i,则四个方向的移动可表示为:
1: (i,j)→(i+2,j+1); (i<3,j<8)
2: (i,j)→(i+1,j+2); (i<4,j<7)
3: (i,j)→(i-1,j+2); (i>0,j<7)
4: (i,j)→(i-2,j+1); (i>1,j<8)
搜索策略:
S1:A[1]:=(0,0);
S2:从A[1]出发,按移动规则依次选定某个方向,如果达到的是(4,8)则转向S3,否则继续搜索下一个到达的顶点;
S3:打印路径。
#include<cstdio>
#include<iostream>
#include<cstdlib>
using namespace std;
int a[100][100],t=0; //路径总数和路径
int x[4]={2,1,-1,-2}, //四种移动规则
y[4]={1,2,2,1};
int search(int); //搜索
int print(int); //打印
int main() //主程序
{
a[1][1]=0;a[1][2]=0; //从坐标(0,0)开始往右跳第二步
search(2);
system("pause");
};
int search(int i)
{
for (int j=0;j<=3;j++) //往4个方向跳
if (a[i-1][1]+x[j]>=0&&a[i-1][1]+x[j]<=4
&&a[i-1][2]+y[j]>=0&&a[i-1][2]+y[j]<=8) //判断马不越界
{
a[i][1]=a[i-1][1]+x[j]; //保存当前马的位置
a[i][2]=a[i-1][2]+y[j];
if (a[i][1]==4&&a[i][2]==8) print(i);
else search(i+1); //搜索下一步
}
}
int print(int ii)
{
{
t++;
cout<<t<<": ";
for (int i=1;i<=ii-1;i++)
cout<<a[i][1]<<","<<a[i][2]<<"-->";
cout<<"4,8"<<endl;
}
}【例6】设有A,B,C,D,E五人从事J1,J2,J3,J4,J5五项工作,每人只能从事一项,他们的效益如下。
每人选择五项工作中的一项,在各种选择的组合中,找到效益最高的的一种组合输出。
【算法分析】
⒈用数组f储存工作选择的方案;数组g存放最优的工作选择方案;数组p用于表示某项工作有没有被选择了。
⒉(1)选择p(i)=0的第i项工作;
(2)判断效益是否高于max已记录的效益,若高于则更新g数组及max的值。
⒊搜索策略: 回溯法(深度优先搜索dfs)。
【参考程序】
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<iomanip>
using namespace std;
int data[6][6]={{0,0,0,0,0,0},{0,13,11,10,4,7},{0,13,10,10,8,5},{0,5,9,7,7,4},{0,15,12,10,11,5},{0,10,11,8,8,4}};
int max1=0,g[10],f[10];
bool p[6]={0};
int go(int step,int t) // step是第几个人,t是之前已得的效益
{
for (int i=1;i<=5;i++)
if (!p[i]) //判断第i项工作没人选择
{
f[step]=i; //第step个人,就选第i项工作
p[i]=1; //标记第i项工作被人安排了
t+=data[step][i]; //计算效益值
if (step<5) go(step+1,t);
else if (t>max1) //保存最佳效益值
{
max1=t;
for (int j=1;j<=5;j++)
g[j]=f[j]; //保存最优效益下的工作选择方案
}
t-=data[step][i]; //回溯
p[i]=0;
}
}
int main()
{
go(1,0); //从第1个人,总效益为0开始
for (int i=1;i<=5;i++)
cout<<char(64+i)<<":J"<<g[i]<<setw(3); //输出各项工作安排情况
cout<<endl;
cout<<"supply:"<<max1<<endl; //输出最佳效益值
}【例7】选书
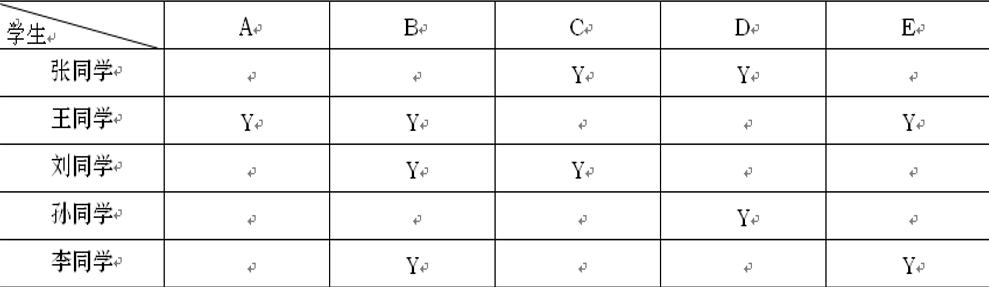
学校放寒假时,信息学竞赛辅导老师有A,B,C,D,E五本书,要分给参加培训的张、王、刘、孙、李五位同学,每人只能选一本书。老师事先让每个人将自己喜欢的书填写在如下的表格中。然后根据他们填写的表来分配书本,希望设计一个程序帮助老师求出所有可能的分配方案,使每个学生都满意。
【算法分析】
可用穷举法,先不考虑“每人都满意” 这一条件,这样只剩“每人选一本且只能选一本”这一条件。在这个条件下,可行解就是五本书的所有全排列,一共有5!=120种。然后在120种可行解中一一删去不符合“每人都满意”的解,留下的就是本题的解答。
为了编程方便,设1,2,3,4,5分别表示这五本书。这五个数的一种全排列就是五本书的一种分发。例如54321就表示第5本书(即E)分给张,第4本书(即D)分给王,……,第1本书(即A)分给李。“喜爱书表”可以用二维数组来表示,1表示喜爱,0表示不喜爱。
算法设计:S1:产生5个数字的一个全排列;
S2:检查是否符合“喜爱书表”的条件,如果符合就打印出来;
S3:检查是否所有的排列都产生了,如果没有产生完,则返回S1;
S4:结束。
上述算法有可以改进的地方。比如产生了一个全排列12345,从表中可以看出,选第一本书即给张同学的书,1是不可能的,因为张只喜欢第3、4本书。这就是说,1××××一类的分法都不符合条件。
由此想到,如果选定第一本书后,就立即检查一下是否符合条件,发现1是不符合的,后面的四个数字就不必选了,这样就减少了运算量。
换句话说,第一个数字只在3、4中选择,这样就可以减少3/5的运算量。
同理,选定了第一个数字后,也不应该把其他4个数字一次选定,而是选择了第二个数字后,就立即检查是否符合条件。
例如,第一个数选3,第二个数选4后,立即检查,发现不符合条件,就应另选第二个数。这样就把34×××一类的分法在产生前就删去了。又减少了一部分运算量。
综上所述,改进后的算法应该是:在产生排列时,每增加一个数,就检查该数是否符合条件,不符合,就立刻换一个,符合条件后,再产生下一个数。因为从第I本书到第I+1本书的寻找过程是相同的,所以可以用回溯算法。算法设计如下:
int Search(i)
{
for (j=1;j<=5;j++)
{
if (第i个同学分给第j本书符合条件)
{
记录第i个数
if (i==5) 打印一个解;
else Search(i+1);
删去第i 个数
}
}
}
【参考程序】
#include<cstdio>
#include<iostream>
#include<cstdlib>
using namespace std;
int book[6],c;
bool flag[6],like[6][6]={{0,0,0,0,0,0},{0,0,0,1,1,0},{0,1,1,0,0,1},
{0,0,1,1,0,0},{0,0,0,0,1,0},{0,0,1,0,0,1}};;
int search(int);
int print();
int main()
{
for (int i=1;i<=5;i++) flag[i]=1;
search(1); //从第1个开始选书,递归。
system("pause");
}
int search(int i) //递归函数
{
for (int j=1;j<=5; j++) //每个人都有5本书可选
if (flag[j]&&like[i][j]) //满足分书的条件
{
flag[j]=0; //把被选中的书放入集合flag中,避免重复被选
book[i]=j; //保存第i个人选中的第j本书
if (i==5) print(); //i=5时,所有的人都分到书,输出结果
else search(i+1); //i<5时,继续递归分书
flag[j]=1; //回溯:把选中的书放回,产生其他分书的方案
book[i]=0;
}
}
int print()
{
c++; //方案数累加1
cout <<"answer " <<c <<":\n";
for (int i=1;i<=5;i++)
cout <<i <<": " <<char(64+book[i]) <<endl; //输出分书的方案
}
输出结果:
zhang: C
wang: A
liu: B
sun: D
li: E
【例8】跳马问题。在5*5格的棋盘上,有一只中国象棋的马,从(1,1)点出发,按日字跳马,它可以朝8个方向跳,但不允许出界或跳到已跳过的格子上,要求在跳遍整个棋盘。
输出前5个方案及总方案数。
输出格式示例:
1 16 21 10 25
20 11 24 15 22
17 2 19 6 9
12 7 4 23 14
3 18 13 8 5
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<iomanip>
using namespace std;
int u[8]={1,2,2,1,-1,-2,-2,-1}, //8个方向上的x,y增量
v[8]={-2,-1,1,2,2,1,-1,-2};
int a[100][100]={0},num=0; //记每一步走在棋盘的哪一格和棋盘的每一格有
//没有被走过
bool b[100][100]={0};
int search(int,int,int); //以每一格为阶段,在每一阶段中试遍8个方向
int print(); //打印方案
int main()
{
a[1][1]=1;b[1][1]=1; //从(1,1)第一步开始走
search(1,1,2); //从(1,1)开始搜第2步该怎样走
cout<<num<<endl; //输出总方案(304)
system("pause");
}
int search(int i,int j,int n)
{
int k,x,y; //这三个变量一定要定义局部变量
if (n>25) {print();return 0;} //达到最大规模打印、统计方案
for (k=0;k<=7;k++) //试遍8个方向
{
x=i+u[k];y=j+v[k]; //走此方向,得到的新坐标
if (x<=5&&x>=1&&y<=5&&y>=1&&(!b[x][y]))
{ //如果新坐标在棋盘上,并且这一格可以走
b[x][y]=1;
a[x][y]=n;
search(x,y,n+1); //从(x,y)去搜下一步该如何走
b[x][y]=0;
a[x][y]=0;
}
}
}
int print()
{
num++; //统计总方案
if (num<=5) //打印出前5种方案
{
for (int k=1;k<=5;k++) //打印本次方案
{
for (int kk=1;kk<=5;kk++)
cout<<setw(5)<<a[k][kk];
cout<<endl;
}
}
}【例9】数的划分(NOIP2001)**
【问题描述】
将整数n分成k份,且每份不能为空,任意两种分法不能相同(不考虑顺序)。例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5; 1,5,1; 5,1,1;
问有多少种不同的分法。
【输入格式】
n,k (6<n≤200,2≤k≤6)
【输出格式】
一个整数,即不同的分法。
【输入样例】
7 3
【输出样例】
4
{ 4种分法为:1,1,5;1,2,4;1,3,3; 2,2,3 说明部分不必输出 }
方法1、回溯法,超时,参考程序如下。
#include<cstdio>
#include<iostream>
#include<cstdlib>
using namespace std;
int n,i,j,k,rest,sum,total;
int s[7];
int main()
{
cout << "Input n k";
cin >> n >> k;
total = 0; s[1] = 0;
i = 1;
while (i)
{
s[i]++;
if (s[i] > n) i--;
else if (i == k)
{
sum = 0;
for (j = 1; j <= k; j++) sum += s[j];
if (n == sum) total++;
}
else {
rest -= s[i];
i++;
s[i] = s[i-1] - 1;
}
}
cout << total;
system("pause");
return 0;
}
方法2、递归,参考程序如下。
#include<cstdio>
#include<iostream>
#include<cstdlib>
using namespace std;
int n,k;
int f(int a,int b,int c)
{
int g = 0,i;
if (b == 1) g = 1;
else for (i = c; i <= a/b; i++)
g += f(a-i,b-1,i);
return g;
}
int main()
{
cout << "Input n,k:";
cin >> n >> k;
cout << f(n,k,1);
system("pause");
return 0;
}
方法3、用动态循环穷举所有不同的分解,要注意剪枝,参考程序如下。
#include<cstdio>
#include<iostream>
#include<cstdlib>
using namespace std;
int n,k,total;
int min(int x,int y)
{
if (x < y) return x;
else return y;
}
void select(int dep,int rest,int last)
{
int i;
if (dep == 0) total++;
else for (i = min(rest-dep+1,last); i >= rest/dep; i--)
select(dep-1,rest-i,i);
}
int main()
{
cout << "Input n,k:";
cin >> n >> k;
total = 0;
select(k,n,n);
cout << total;
system("pause");
return 0;
}
方法4、递推法
首先将正整数n分解成k个正整数之和的不同分解方案总数等于将正整数n-k分解成任意个不大于k的正整数之和的不同分解方案总数(可用ferror图证明之),后者的递推公式不难得到,参考程序如下。
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
using namespace std;
int i,j,k,n,x;
int p[201][7];
int main()
{
cin >> n >> k;
memset(p,0,sizeof(p));
p[0][0] = 1;
for (i = 1; i <= n; i++) p[i][1] = 1;
for (i = 1; i <= n - k; i++)
for (j = 2; j <= min(i,k); j++)
for (x = 1; x <= min(i,j); x++)
p[i][j] += p[i-x][min(i-x,x)];
cout << p[n-k][k];
system("pause");
return 0;
}