README_EN.md

2943. Maximize Area of Square Hole in Grid

中文文档

Description

There is a grid with n + 2 horizontal bars and m + 2 vertical bars, and initially containing 1 x 1 unit cells.

The bars are 1-indexed.

You are given the two integers, n and m.

You are also given two integer arrays: hBars and vBars.

• hBars contains distinct horizontal bars in the range [2, n + 1].
• vBars contains distinct vertical bars in the range [2, m + 1].

You are allowed to remove bars that satisfy any of the following conditions:

• If it is a horizontal bar, it must correspond to a value in hBars.
• If it is a vertical bar, it must correspond to a value in vBars.

Return an integer denoting the maximum area of a square-shaped hole in the grid after removing some bars (possibly none).

 

Example 1:

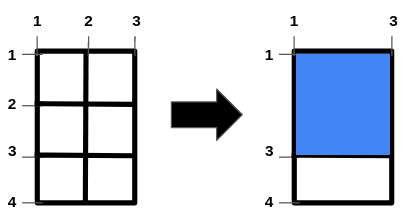
Input: n = 2, m = 1, hBars = [2,3], vBars = [2]
Output: 4
Explanation: The left image shows the initial grid formed by the bars.
The horizontal bars are in the range [1,4], and the vertical bars are in the range [1,3].
It is allowed to remove horizontal bars [2,3] and the vertical bar [2].
One way to get the maximum square-shaped hole is by removing horizontal bar 2 and vertical bar 2.
The resulting grid is shown on the right.
The hole has an area of 4.
It can be shown that it is not possible to get a square hole with an area more than 4.
Hence, the answer is 4.

Example 2:

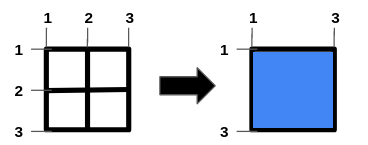
Input: n = 1, m = 1, hBars = [2], vBars = [2]
Output: 4
Explanation: The left image shows the initial grid formed by the bars.
The horizontal bars are in the range [1,3], and the vertical bars are in the range [1,3].
It is allowed to remove the horizontal bar [2] and the vertical bar [2].
To get the maximum square-shaped hole, we remove horizontal bar 2 and vertical bar 2.
The resulting grid is shown on the right.
The hole has an area of 4.
Hence, the answer is 4, and it is the maximum possible.

Example 3:

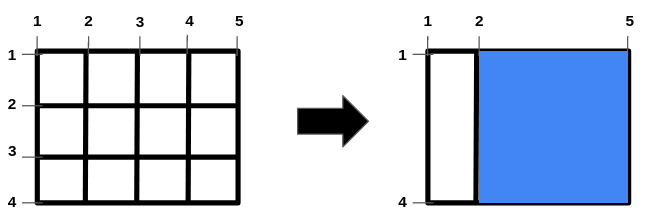
Input: n = 2, m = 3, hBars = [2,3], vBars = [2,3,4]
Output: 9
Explanation: The left image shows the initial grid formed by the bars.
The horizontal bars are in the range [1,4], and the vertical bars are in the range [1,5].
It is allowed to remove horizontal bars [2,3] and vertical bars [2,3,4].
One way to get the maximum square-shaped hole is by removing horizontal bars 2 and 3, and vertical bars 3 and 4.
The resulting grid is shown on the right.
The hole has an area of 9.
It can be shown that it is not possible to get a square hole with an area more than 9.
Hence, the answer is 9.

 

Constraints:

• 1 <= n <= 109
• 1 <= m <= 109
• 1 <= hBars.length <= 100
• 2 <= hBars[i] <= n + 1
• 1 <= vBars.length <= 100
• 2 <= vBars[i] <= m + 1
• All values in hBars are distinct.
• All values in vBars are distinct.

Solutions

Solution 1: Sorting

The problem essentially asks us to find the length of the longest consecutive increasing subsequence in the array, and then add 1 to it.

We define a function $f(nums)$, which represents the length of the longest consecutive increasing subsequence in the array $nums$.

For the array $nums$, we first sort it, then traverse the array. If the current element $nums[i]$ equals the previous element $nums[i - 1]$ plus 1, it means that the current element can be added to the consecutive increasing subsequence. Otherwise, it means that the current element cannot be added to the consecutive increasing subsequence, and we need to start calculating the length of the consecutive increasing subsequence again. Finally, we return the length of the consecutive increasing subsequence plus 1.

After finding the length of the longest consecutive increasing subsequence in $hBars$ and $vBars$, we take the minimum of the two as the side length of the square, and then calculate the area of the square.

The time complexity is $O(n \times \log n)$, and the space complexity is $O(n)$. Here, $n$ is the length of the array $hBars$ or $vBars$.

class Solution:
    def maximizeSquareHoleArea(
        self, n: int, m: int, hBars: List[int], vBars: List[int]
    ) -> int:
        def f(nums: List[int]) -> int:
            nums.sort()
            ans = cnt = 1
            for i in range(1, len(nums)):
                if nums[i] == nums[i - 1] + 1:
                    cnt += 1
                    ans = max(ans, cnt)
                else:
                    cnt = 1
            return ans + 1

        return min(f(hBars), f(vBars)) ** 2

class Solution {
    public int maximizeSquareHoleArea(int n, int m, int[] hBars, int[] vBars) {
        int x = Math.min(f(hBars), f(vBars));
        return x * x;
    }

    private int f(int[] nums) {
        Arrays.sort(nums);
        int ans = 1, cnt = 1;
        for (int i = 1; i < nums.length; ++i) {
            if (nums[i] == nums[i - 1] + 1) {
                ans = Math.max(ans, ++cnt);
            } else {
                cnt = 1;
            }
        }
        return ans + 1;
    }
}

class Solution {
public:
    int maximizeSquareHoleArea(int n, int m, vector<int>& hBars, vector<int>& vBars) {
        auto f = [](vector<int>& nums) {
            int ans = 1, cnt = 1;
            sort(nums.begin(), nums.end());
            for (int i = 1; i < nums.size(); ++i) {
                if (nums[i] == nums[i - 1] + 1) {
                    ans = max(ans, ++cnt);
                } else {
                    cnt = 1;
                }
            }
            return ans + 1;
        };
        int x = min(f(hBars), f(vBars));
        return x * x;
    }
};

func maximizeSquareHoleArea(n int, m int, hBars []int, vBars []int) int {
	f := func(nums []int) int {
		sort.Ints(nums)
		ans, cnt := 1, 1
		for i, x := range nums[1:] {
			if x == nums[i]+1 {
				cnt++
				ans = max(ans, cnt)
			} else {
				cnt = 1
			}
		}
		return ans + 1
	}
	x := min(f(hBars), f(vBars))
	return x * x
}

function maximizeSquareHoleArea(n: number, m: number, hBars: number[], vBars: number[]): number {
    const f = (nums: number[]): number => {
        nums.sort((a, b) => a - b);
        let [ans, cnt] = [1, 1];
        for (let i = 1; i < nums.length; ++i) {
            if (nums[i] === nums[i - 1] + 1) {
                ans = Math.max(ans, ++cnt);
            } else {
                cnt = 1;
            }
        }
        return ans + 1;
    };
    return Math.min(f(hBars), f(vBars)) ** 2;
}

impl Solution {
    pub fn maximize_square_hole_area(n: i32, m: i32, h_bars: Vec<i32>, v_bars: Vec<i32>) -> i32 {
        let f = |nums: &mut Vec<i32>| -> i32 {
            let mut ans = 1;
            let mut cnt = 1;
            nums.sort();
            for i in 1..nums.len() {
                if nums[i] == nums[i - 1] + 1 {
                    cnt += 1;
                    ans = ans.max(cnt);
                } else {
                    cnt = 1;
                }
            }
            ans + 1
        };

        let mut h_bars = h_bars;
        let mut v_bars = v_bars;
        let x = f(&mut h_bars).min(f(&mut v_bars));
        x * x
    }
}